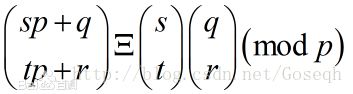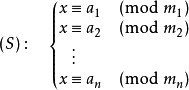基础数论算法详解
基础数论算法
首先,它们这些算法十分基础,基础到并不包含莫比乌斯反演什么的,所以仅仅当做娱乐性质的文章
内容一览
由于数论中的算法较多,下面先进行一个小汇总
素数的筛法
最大公约数求法
扩展 GCD 算法
质因数分解法
乘法逆元求法
组合数计算方法
Lucas 定理
中国剩余定理
线性一次同余式解法
等比数列求和(当然这应该不是数论)
当然啦,都是一些比较基础的东西,意思是需要数学基础的东西
下面将进行逐个讲解
详解
素数的筛法
原理
我们很多时候用的是朴素的质数筛法,即我们按照2到 n 进行筛去,记录一个 vis 数组表示当前数是否为质数即可
代码
但是还有一种 O(n) 的方法,即欧拉筛法,每次让每一个数只被它所含有的最小的质因子筛去,详情见代码
代码
void construct_prime_table(LL range){
for(LL i=2;iif(!vis[i])pt[cnt++]=i;
for(int j=0;jif(i*pt[j]>=range)break;
vis[i*pt[j]]=1;
if(i%pt[j]==0)break;
}
}
} 最大公约数(GCD)
原理
这个东西其实非常简单啦,我们可以使用辗转相除法或是更相减损法,但是下面只贴辗转相除法的代码,而更相减损法也有它的用武之地,那就是在求两个巨大的高精度数的时候,用于 Stein 算法,其他文章会予以介绍
下面贴代码
代码
LL gcd(LL x,LL y){
if(y==0)return x;
return gcd(y,x%y);
}扩展GCD算法
原理
主要是来源于数论中的裴蜀定理,然后思路与原GCD十分相近,可以求出使得
ax+by=gcd(x,y)
成立且 |a|+|b| 最小的一组解 (a,b)
下面贴代码
代码
void patulous_gcd(LL a,LL b,LL& d,LL& x,LL& y){
if(b==0){d=a;x=1;y=0;return;}
patulous_gcd(b,a%b,d,y,x);y-=a/b*x;
}质因数分解法
原理
这里介绍朴素的算法,即 O(n√) 的那个,虽然有更先进的算法,但是我并不会,下面直接贴代码
代码
void prime_factorization(LL x){
for(LL i=2;i<=(LL)sqrt(x);i++){
if(vis[i]||x%i!=0)continue;
mod[size]=1;
while(x>1&&x%i==0){
mod[size]*=i;
x=x/i;
}
size++;
}
if(x>1)mod[size++]=x;
}乘法逆元的求法
原理
我们可以用一种神奇的方式来以 O(M) 的复杂度生成一个模数M(为质数)的所有逆元,考虑这样的式子:
ax+b≡0(modM) (注意那个是同余符号)
等式左右同时乘以 x−1b−1 ,则有
a∗b−1+x−1≡0(modM)
即 x−1≡−a∗b−1(modM)
这样我们就成功地求出了 x 的模 M 意义下的逆元
代码如下
代码
void get_all_multiplicative_inverse(LL M){
inv[1]=1;
for(LL i=2;i原理
但是如果我们只想要一个逆元怎么办?
我们可以考虑如下同余式:
aa−1≡1(modM)
即有 a∗a−1+b∗M=1 (注意这个时候是等于号)
这样,我们便可以使用扩展GCD啦
代码
LL get_single_multiplicative_inverse(LL a,LL M){
LL d,x,y;
patulous_gcd(a,M,d,x,y);
return (x%M+M)%M;
}组合数计算方法
原理
大家应该都知道组合数是怎么算的,然而那个除来除去的部分我们都很讨厌,所以我们可以使用逆元来搞定它,即乘上这个数的逆元模 M 等于除以这个数模 M
代码
LL calculate_combination_number(LL m,LL n,LL k){
if(mreturn 0;
LL ans=1;
//get_all_multiplicative_inverse(k);
for(LL i=1;i<=n;i++){
ans=(ans*(inv[i]*(i+m-n))%k)%k;
}
return ans;
} Lucas 定理
原理
就是这样的一个小式子:
(百度百科直下)
直接贴代码
代码
LL Lucas(LL m,LL n,LL k){
if(mreturn calculate_combination_number(m,n,k);
}
return (Lucas(m/k,n/k,k)*Lucas(m%k,n%k,k))%k;
} 线性同余式解法
原理
就是考虑如下的一个式子:
ax≡b(modM)
我们只要等式两端同乘 a−1 即可
即 x≡a−1b(modM)
下面贴代码
代码
LL solve_congruence(LL a,LL b,LL m){
LL _a=get_single_multiplicative_inverse(a,m);
return (b*_a)%m;
}中国剩余定理
原理
额。。。写这文章简直是要累死啦。。。
就是说现在我们手头有一组线性同余式,它们的模数都是互质的,我们要求这个方程组的解,那么我们可以使用中国剩余定理,它常常被用于模数不是质数的情况,这个时候我们就需要用中国剩余定理来求出答案
大致是这样的:
真是服了这个markdown里似是非是的Latex了,根本打不出来上面的好吗
然后,我们可以很轻松的发现:
![]()
是唯一解,这个只要有点数学基础的应该都会证(但是我不会)
这样就搞定啦O(∩_∩)O
下面是代码
代码
LL chinese_remainder_theorem(LL x){
LL ans=0;
prime_factorization(M);
calculate_array_a();//计算a数组
ans=(((M/mod[i]*a[i]*get_single_multiplicative_inverse(M/mod[i],mod[i]))%M+ans)%M+M)%M;
}
return ans;
}等比数列求和
原理
应该都会吧,是吧= =
代码
LL calculate_geometric_progression(LL first,LL ratio,LL num){
return (((get_power(ratio,num+1)-1)*inv[ratio-1])%M*first)%M;
}其中 get _ power() 用于求幂
总结
我的天终于写完了。。。总之每个部分都是看起来简单用起来难,因为常常要做一些改动,同时要把许多部分组合在一起,这样就非常的麻烦了,还有一些比如什么MR判素啊,高级的质因数分解啊以后再说吧,放在高级数论里搞