三维空间刚体运动——视觉SLAM十四讲笔记
三维空间的刚体运动
- 点与坐标系
- 旋转矩阵
- 旋转向量和欧拉角
- 四元数
点与坐标系
2D的情况:用两个坐标加旋转角表达
3D的情况:?
在描述3D的情况前,可以先描述一些基本概念:
坐标系、点、向量、向量的坐标
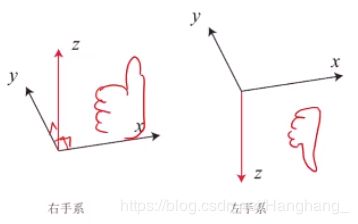
坐标系(参考系)任何运动都是相对的,需要一个参考系。只能说哪个东西在某个参考系下看起来是怎样的运动、它位于什么位置等等。参考系一般是由三个轴组成的迁移空间的一个基,基向量,正常情况下这三个基向量都是彼此正交的。有两种不同的定义方式,左手系和右手系,除大拇指外的四个指头从x转到y,大拇指的方向如果向上就是右手系,反之左手系,两种方式没有优劣之分,在这里我们采用右手系。
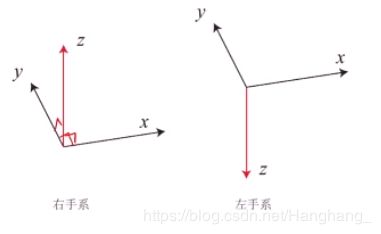
若要讨论运动,一般是在坐标系讨论的。而且往往会讨论到几个坐标系,有一些坐标系是固定的,一些坐标系是运动的,一般我们关心多少个物体就考虑多少个坐标系。
比如一个相机在世界当中运动,这时候建立两个坐标系。一个是世界坐标系,一个是相机坐标系。
我们要关心的是这两个坐标系之间的变换是怎么样子的。
例如:建立一个点P,这个点在两个坐标系的位置是不一样的,已知P在世界坐标轴的位置,如何去变换到相机坐标轴下的坐标?
如果是一个机器人的话,那这样会更加复杂,比如机器人本体需要建立一个坐标系,机械臂也需要建立一个坐标系,激光雷达也会有一个坐标系。如果知道每一个坐标系的位置坐标关系,就可以很方便地讨论某一个数据在一个坐标系下的运动情况,在另一个坐标系下的运动情况。
在世界坐标系中,由于坐标系由三个互相正交的向量基组成,向量P可以由三个基的线性组合所构成,且唯一。向量表示为: P = a 1 x + a 2 y + a 3 z = ( a 1 a 2 a 3 ) T ( x y z ) P=a_1x + a_2y + a_3z = \left(\begin{array}{ccc}{a_1} & {a_2} & {a_3} \\ \end{array}\right)^{T} \left(\begin{array}{ccc}{x} & {y} & {z} \\ \end{array}\right) P=a1x+a2y+a3z=(a1a2a3)T(xyz) 然后我们就可以讨论同样的一个P,它在另一个坐标系下是如何表示的,这几个坐标之间是如何 这是本节所要讨论的问题。
向量的运算可由坐标运算表达
加法和减法
其中两向量的加法和减法,可以使用平行四边形法则来表示。
内积 : 点乘
a ⋅ b = a T b = ∑ i = 1 3 a i b i = ∣ a ∥ b ∣ cos ⟨ a , b ⟩ \boldsymbol{a} \cdot \boldsymbol{b}=\boldsymbol{a}^{T} \boldsymbol{b}=\sum_{i=1}^{3} a_{i} b_{i}=|\boldsymbol{a} \| \boldsymbol{b}| \cos \langle\boldsymbol{a}, \boldsymbol{b}\rangle a⋅b=aTb=i=1∑3aibi=∣a∥b∣cos⟨a,b⟩
外积 : 叉乘
a × b = [ i j k a 1 a 2 a 3 b 1 b 2 b 3 ] = [ a 2 b 3 − a 3 b 2 a 3 b 1 − a 1 b 3 a 1 b 2 − a 2 b 1 ] = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] b ≜ a ∧ b \boldsymbol{a} \times \boldsymbol{b}=\left[\begin{array}{ccc}{i} & {j} & {k} \\ {a_{1}} & {a_{2}} & {a_{3}} \\ {b_{1}} & {b_{2}} & {b_{3}}\end{array}\right]=\left[\begin{array}{c}{a_{2} b_{3}-a_{3} b_{2}} \\ {a_{3} b_{1}-a_{1} b_{3}} \\ {a_{1} b_{2}-a_{2} b_{1}}\end{array}\right]=\left[\begin{array}{ccc}{0} & {-a_{3}} & {a_{2}} \\ {a_{3}} & {0} & {-a_{1}} \\ {-a_{2}} & {a_{1}} & {0}\end{array}\right] b \triangleq a^{\wedge} b a×b=⎣⎡ia1b1ja2b2ka3b3⎦⎤=⎣⎡a2b3−a3b2a3b1−a1b3a1b2−a2b1⎦⎤=⎣⎡0a3−a2−a30a1a2−a10⎦⎤b≜a∧b
会根据右手法则得到一个同时与a和b都垂直的一个向量
这个运算也可以由行列式的方式写出来,右式由i,j,k的分量表示。
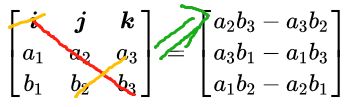
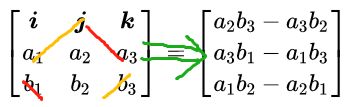

其中,反对称矩阵的形式如下: [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] \left[\begin{array}{ccc}{0} & {-a_{3}} & {a_{2}} \\ {a_{3}} & {0} & {-a_{1}} \\ {-a_{2}} & {a_{1}} & {0}\end{array}\right] ⎣⎡0a3−a2−a30a1a2−a10⎦⎤
有如下性质: p 2 = [ 1.08228 , 0.663509 , 0.686957 ] T p_{2}=[1.08228,0.663509,0.686957]^{T} p2=[1.08228,0.663509,0.686957]T
在了解向量得到运算之后,来探讨以下问题。
如何描述坐标系与坐标系之间的变化?
如何计算同一个向量在不同坐标系里的坐标?
坐标系之间的变化可以直观地表示为:原点间的平移+三个轴的旋转
那么平移是向量,旋转是什么?
旋转矩阵
考虑一次旋转:
坐标系(e1,e2,e3)发生了旋转,变成(e1`,e2`,e3`)
向量α不动,那么它的坐标如何变化?
假设有一点P的坐标位置在世界坐标轴是已知的, P = a 1 x + a 2 y + a 3 z = ( a 1 a 2 a 3 ) T ( x y z ) P=a_1x + a_2y + a_3z = \left(\begin{array}{ccc}{a_1} & {a_2} & {a_3} \\ \end{array}\right)^{T} \left(\begin{array}{ccc}{x} & {y} & {z} \\ \end{array}\right) P=a1x+a2y+a3z=(a1a2a3)T(xyz)由于P是不变的,于是有 [ e 1 , e 2 , e 3 ] [ a 1 a 2 a 3 ] = [ e 1 ′ , e 2 ′ , e 3 ′ ] [ a 1 ′ a 2 ′ a 3 ′ ] \left[e_{1}, e_{2}, e_{3}\right]\left[\begin{array}{l}{a_{1}} \\ {a_{2}} \\ {a_{3}}\end{array}\right]=\left[e_{1}^{\prime}, e_{2}^{\prime}, e_{3}^{\prime}\right]\left[\begin{array}{l}{a_{1}^{\prime}} \\ {a_{2}^{\prime}} \\ {a_{3}^{\prime}}\end{array}\right] [e1,e2,e3]⎣⎡a1a2a3⎦⎤=[e1′,e2′,e3′]⎣⎡a1′a2′a3′⎦⎤
两边同时乘以(e1T e2T e3T)T,其中左边e1T乘以e1为1,e1T乘以e2T和e3T为0,以此类推,(e1T e2T e3T)T乘以[e1,e2,e3]为E单位矩阵,等式如下所示:
[ a 1 a 2 a 3 ] = [ e 1 T e 1 ′ e 1 T e 2 ′ e 1 T e 3 ′ e 2 T e 1 ′ e 2 T e 2 ′ e 2 T e 3 ′ e 3 T e 1 ′ e 3 T e 2 ′ e 3 T e 3 ′ ] [ a 1 ′ a 2 ′ a 3 ′ ] ≜ R a ′ \left[\begin{array}{l}{a_{1}} \\ {a_{2}} \\ {a_{3}}\end{array}\right]=\left[\begin{array}{ccc}{e_{1}^{T} e_{1}^{\prime}} & {e_{1}^{T} e_{2}^{\prime}} & {e_{1}^{T} e_{3}^{\prime}} \\ {e_{2}^{T} e_{1}^{\prime}} & {e_{2}^{T} e_{2}^{\prime}} & {e_{2}^{T} e_{3}^{\prime}} \\ {e_{3}^{T} e_{1}^{\prime}} & {e_{3}^{T} e_{2}^{\prime}} & {e_{3}^{T} e_{3}^{\prime}}\end{array}\right]\left[\begin{array}{c}{a_{1}^{\prime}} \\ {a_{2}^{\prime}} \\ {a_{3}^{\prime}}\end{array}\right] \triangleq R a^{\prime} ⎣⎡a1a2a3⎦⎤=⎣⎡e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′⎦⎤⎣⎡a1′a2′a3′⎦⎤≜Ra′
其中, [ a 1 a 2 a 3 ] \left[\begin{array}{l}{a_{1}} \\ {a_{2}} \\ {a_{3}}\end{array}\right] ⎣⎡a1a2a3⎦⎤为旋转之前的坐标, [ a 1 ′ a 2 ′ a 3 ′ ] \left[\begin{array}{l}{a_{1}^{\prime}} \\ {a_{2}^{\prime}} \\ {a_{3}^{\prime}}\end{array}\right] ⎣⎡a1′a2′a3′⎦⎤为旋转之后的坐标,那么就可以将上式简写成: α = Rα`,其中R就称为旋转矩阵。
可以验证:R是一个正交矩阵( R − 1 = R T ; R T R = I R^{-1} = R^{T};R^{T}R = I R−1=RT;RTR=I(单位矩阵)),R的行列式为+1。
反过来说,满足这两个性质的矩阵称为旋转矩阵。
可以把旋转矩阵的集合形式定义如下:
S O ( n ) = { R ∈ R n × n ∣ R R T = I , det ( R ) = 1 } S O(n)=\left\{\boldsymbol{R} \in \mathbb{R}^{n \times n} | \boldsymbol{R} \boldsymbol{R}^{T}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right\} SO(n)={R∈Rn×n∣RRT=I,det(R)=1}
我们生活在三维空间,所以主要讨论SO(3).
注:SO :Special Orthogonal Group 特殊正交群
两个坐标系的运动,就可以由旋转加平移描述 : a ′ = R a + t \boldsymbol{a}^{\prime}=\boldsymbol{R} \boldsymbol{a}+\boldsymbol{t} a′=Ra+t,两个坐标系间的运动可用R,t完全描述,也就是欧拉定理。
齐次坐标与变换坐标
旋转加平移在表达复合情况下有不便之处: c = R 2 ( R 1 a + t 1 ) + t 2 c=R_{2}\left(\boldsymbol{R}_{1} \boldsymbol{a}+\boldsymbol{t}_{1}\right)+\boldsymbol{t}_{2} c=R2(R1a+t1)+t2
我们可以用齐次的形式表达: [ a ′ 1 ] = [ R t 0 T 1 ] [ a 1 ] ≜ T [ a 1 ] \left[\begin{array}{l}{a^{\prime}} \\ {1}\end{array}\right]=\left[\begin{array}{ll}{\boldsymbol{R}} & {\boldsymbol{t}} \\ {\mathbf{0}^{T}} & {1}\end{array}\right]\left[\begin{array}{l}{\boldsymbol{a}} \\ {1}\end{array}\right] \triangleq \boldsymbol{T}\left[\begin{array}{l}{\boldsymbol{a}} \\ {1}\end{array}\right] [a′1]=[R0Tt1][a1]≜T[a1]
就可以这样表示: b ~ = T 1 a ~ , c ~ = T 2 b ~ ⇒ c ~ = T 2 T 1 a ~ \tilde{\boldsymbol{b}}=\boldsymbol{T}_{1} \tilde{\boldsymbol{a}}, \tilde{\boldsymbol{c}}=\boldsymbol{T}_{2} \tilde{\boldsymbol{b}} \quad \Rightarrow \tilde{\boldsymbol{c}}=\boldsymbol{T}_{2} \boldsymbol{T}_{1} \tilde{\boldsymbol{a}} b~=T1a~,c~=T2b~⇒c~=T2T1a~
我们把上述矩阵 T 称为变换矩阵(Transform Matrix),变换矩阵的集合称为特殊欧式群SE(3)(Special Euclidean Group)
S E ( 3 ) = { T = [ R t 0 T 1 ] ∈ R 4 × 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } S E(3)=\left\{\boldsymbol{T}=\left[\begin{array}{cc}{\boldsymbol{R}} & {\boldsymbol{t}} \\ {\mathbf{0}^{T}} & {1}\end{array}\right] \in \mathbb{R}^{4 \times 4} | \boldsymbol{R} \in S O(3), \boldsymbol{t} \in \mathbb{R}^{3}\right\} SE(3)={T=[R0Tt1]∈R4×4∣R∈SO(3),t∈R3}
它的逆形式为: T − 1 = [ R T − R T t 0 T 1 ] \boldsymbol{T}^{-1}=\left[\begin{array}{cc}{\boldsymbol{R}^{T}} & {-\boldsymbol{R}^{T} \boldsymbol{t}} \\ {\mathbf{0}^{T}} & {1}\end{array}\right] T−1=[RT0T−RTt1]
旋转向量和欧拉角
旋转矩阵R有九个元素,但仅有三个自由度,能否以更少的元素表达旋转?
答案是肯定的,除了旋转矩阵,还有旋转向量、欧拉角以及四元数可以表达旋转。
旋转向量:方向为旋转轴,长度为转过的角度 ;称为角轴/轴角(Angle Axis)或旋转向量(Rotation Vector)
旋转向量与矩阵不同:仅有三个量,无约束,更直观
假如知道旋转轴和转过的角度,要计算旋转矩阵R,则需要用到罗德里格斯公式: R = cos θ I + ( 1 − cos θ ) n n T + sin θ n ∧ \boldsymbol{R}=\cos \theta \boldsymbol{I}+(1-\cos \theta) \boldsymbol{n} \boldsymbol{n}^{T}+\sin \theta \boldsymbol{n}^{\wedge} R=cosθI+(1−cosθ)nnT+sinθn∧
角度: θ = arccos ( tr ( R ) − 1 2 ) \theta=\arccos \left(\frac{\operatorname{tr}(\boldsymbol{R})-1}{2}\right) θ=arccos(2tr(R)−1)
轴: R n = n , λ = 1 \boldsymbol{R n}=\boldsymbol{n}, \lambda=1 Rn=n,λ=1为特征向量
**欧拉角:**将旋转分解为为三个方向上的转动,轴可以是定轴或动轴(转之前的x轴或转之后的x轴),顺序亦可不同。常见的有yaw-pitch-roll(Z-Y-X)。使用欧拉角优点是非常直观,缺点是定义非常混乱,使用比较复杂,还有一个严重的问题就是万向锁(Gimbal Lock),在某种特定的情况下,会出现奇异性,就是减少掉一个自由度。
比如 Yaw-Pitch-Roll 顺序下,当Pitch为90度时,存在奇异性,即yaw和roll方向一样。
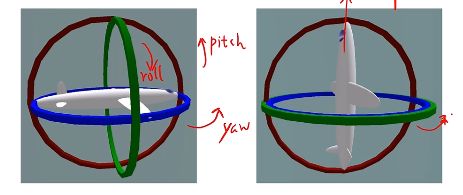
由于万向锁的存在,欧拉角不适合插值或迭代,多用于人机交互中,可以证明:仅用三个实数表达旋转时,不可避免地存在奇异性问题,所以SLAM中也很少用欧拉角表示姿态。
四元数
四元数是一种既比较节省空间又不带奇异性的表达旋转的方法。
在2D情况下,可用 单位复数表达旋转。复数是二维的,在复平面上,实数可用一条从左到右的直线表示,而虚数可以由一条从小至上的直线表示。

z = x + i y = ρ e i θ z=x+i y=\rho e^{i \theta} z=x+iy=ρeiθ
已知i² = -1 。 4 × i × i = -4 ,意思就是4在数轴上旋转了180°
而 4 × i = 4i 意思是旋转了90度。
如下图所示: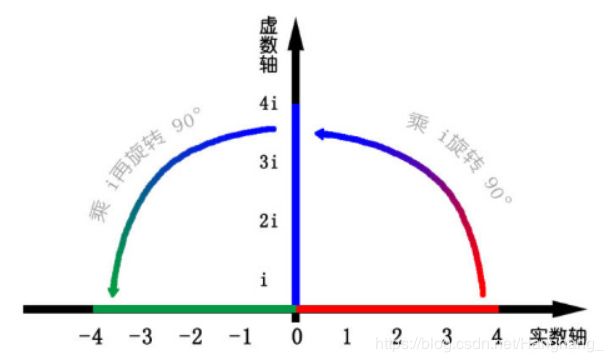
在三维的情况下, 四元数可作为复数的扩充。
四元数有三个虚部和一个实部: q = q 0 + q 1 i + q 2 j + q 3 k \boldsymbol{q}=q_{0}+q_{1} i+q_{2} j+q_{3} k q=q0+q1i+q2j+q3k
三个虚部很像三维空间中的三个坐标轴: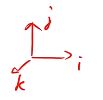
虚部之间满足关系: { i 2 = j 2 = k 2 = − 1 i j = k , j i = − k j k = i , k j = − i k i = j , i k = − j \left\{\begin{array}{l}{i^{2}=j^{2}=k^{2}=-1} \\ {i j=k, j i=-k} \\ {j k=i, k j=-i} \\ {k i=j, i k=-j}\end{array}\right. ⎩⎪⎪⎨⎪⎪⎧i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−j
自己和自己的运算像复数(如i² = k² = j² = -1),自己和别人的运算像叉乘 (ij = k ; ji = -k)(两向量的叉乘所得向量是垂直于两向量的)。
单位四元数可以表示旋转: q = [ s , v ] , s = q 0 ∈ R , v = [ q 1 , q 2 , q 3 ] T ∈ R 3 \boldsymbol{q}=[s, \boldsymbol{v}], \quad s=q_{0} \in \mathbb{R}, \boldsymbol{v}=\left[q_{1}, q_{2}, q_{3}\right]^{T} \in \mathbb{R}^{3} q=[s,v],s=q0∈R,v=[q1,q2,q3]T∈R3
学完了旋转向量、欧拉角和四元数,我们还得了解他们之间的转换。
四元数到角轴: q = [ cos θ 2 , n x sin θ 2 , n y sin θ 2 , n z sin θ 2 ] T \boldsymbol{q}=\left[\cos \frac{\theta}{2}, n_{x} \sin \frac{\theta}{2}, n_{y} \sin \frac{\theta}{2}, n_{z} \sin \frac{\theta}{2}\right]^{T} q=[cos2θ,nxsin2θ,nysin2θ,nzsin2θ]T
角轴到四元数: { θ = 2 arccos q 0 [ n x , n y , n z ] T = [ q 1 , q 2 , q 3 ] T / sin θ 2 \left\{\begin{array}{l}{\theta=2 \arccos q_{0}} \\ {\left[n_{x}, n_{y}, n_{z}\right]^{T}=\left[q_{1}, q_{2}, q_{3}\right]^{T} / \sin \frac{\theta}{2}}\end{array}\right. {θ=2arccosq0[nx,ny,nz]T=[q1,q2,q3]T/sin2θ
如何用四元数旋转一个空间点?设点P经过一次以q表示的旋转后,得到了P`,他们关系如何表示?
将P的坐标用四元数表示(虚四元数): p = [ 0 , x , y , z ] = [ 0 , v ] p=[0, x, y, z]=[0, v] p=[0,x,y,z]=[0,v]
旋转之后的关系为: p ′ = q p q − 1 p^{\prime}=q p q^{-1} p′=qpq−1
四元数相比于角轴、欧拉角的优势:紧凑、无奇异性。
参考:《视觉slam十四讲》
http://blog.sina.com.cn/s/blog_3ece1f640102xylu.html