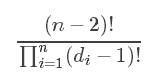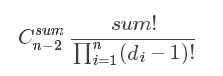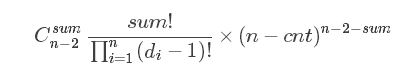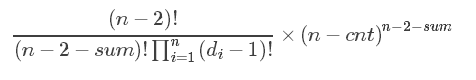bzoj 1005: [HNOI2008]明明的烦恼（prufer数列）

1005: [HNOI2008]明明的烦恼

Time Limit: 1 Sec   Memory Limit: 162 MB
Submit: 5171   Solved: 2021
[ Submit][ Status][ Discuss]

Description

　　自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?

Input

　　第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1

Output

　　一个整数,表示不同的满足要求的树的个数,无解输出0

Sample Input

3

1

-1

-1

Sample Output

2

根据数的度数求数的种类可以用prufer数列

prufer数列是无根树的一种数列。在组合数学中，Prufer数列由有一个对于顶点标过号的树转化来的数列，点数为n的

树转化来的Prufer数列长度为n-2。它可以通过简单的迭代方法计算出来

一种生成Prufer序列的方法是迭代删点，直到原图仅剩两个点。对于一棵顶点已经经过编号的树T，顶点的编号为{1,2,...,n}，在第i步时，移去所有叶子节点（度为1的顶点）中标号最小的顶点和相连的边，并把与它相邻的点的编号加入Prufer序列中，重复以上步骤直到原图仅剩2个顶点。

例子

以下面的树为例子，首先在所有叶子节点中编号最小的点是2，和它相邻的点的编号是3，将3加入序列并删除编号为2的点。接下来删除的点是4，5被加入序列，然后删除5，1被加入序列，1被删除，3被加入序列，此时原图仅剩两个点（即3和6），Prufer序列构建完成，为{3,5,1,3}

性质

1：任意一点的度为d，那么这个数一定会在这个序列中存在d-1个

2：序列和树一一对应

这题我们假设度数已知，第i个点的度数为di，那么我们可以构造出的数列个数（树的个数）就为

可这题我们有些点的度数并不知道，假设我们已知cnt个点的度数，它们的度数之和为sum+cnt，因为序列长度为

n+2，所以无视空位可以构造出的数列个数（树的个数）就为

（其中所有的di都是已知的点的度数）

因为还有n-cut个位置，剩下的每个位置可以放任意一个未知度数的点，所以这题答案就是

冷静的化简下↓

但还没那么简单，很显然这题的答案是个超大的数，需要用到高精度乘法，可由于有分母，所以要将每个元素

都分解质因数，分子的质因数和分母的公共质因数约掉之后再×就好了

注意特判n=1和n=2以及不合法的情况（sum过大或者某个度节点数过大或为0）

#include
#include
int k, a[1005], pri[1005], cot[1005], ans[10005], p[1005] = {1,1};
void Add(int n, int m)
{
	int i;
	if(n==0)
		return;
	for(i=1;i<=k;i++)
	{
		while(n%pri[i]==0)
		{
			n /= pri[i];
			cot[i] += m;
		}
	}
}
int main(void)
{
	int n, i, j, ok, sum, cnt, len;
	k = 0;
	for(i=2;i<=1000;i++)
	{
		if(p[i])
			continue;
		pri[++k] = i;
		for(j=i*i;j<=1000;j+=i)
			p[j] = 1;
	}
	while(scanf("%d", &n)!=EOF)
	{
		ok = 1;
		sum = cnt = 0;
		memset(cot, 0, sizeof(cot));
		for(i=1;i<=n;i++)
		{
			scanf("%d", &a[i]);
			if(a[i]==0 || a[i]>=n)
				ok = 0;
			if(a[i]!=-1)
			{
				cnt++;
				sum += a[i]-1;
				for(j=1;j<=a[i]-1;j++)
					Add(j, -1);
			}
		}
		if(ok==0 || n-2-sum<0)
			printf("0\n");
		else if(n==1)
		{
			if(a[1]<=0)  printf("1\n");
			else  printf("0\n");
		}
		else if(n==2)
		{
			if(a[1]>1 || a[2]>1 || a[1]==0 || a[2]==0)  printf("0\n");
			else  printf("1\n");
		}
		else
		{
			for(i=n-2-sum+1;i<=n-2;i++)
				Add(i, 1);
			Add(n-cnt, n-2-sum);
			memset(ans, 0, sizeof(ans));
			ans[1] = 1, len = 1;
			for(i=1;i<=k;i++)
			{
				while(cot[i])
				{
					cot[i]--;
					for(j=1;j<=len;j++)
						ans[j] *= pri[i];
					for(j=1;j=10)
					{
						ans[len+1] = ans[len]/10;
						ans[len++] %= 10;
					}
				}
			}
			for(i=len;i>=1;i--)
				printf("%d", ans[i]);
			printf("\n");
		}
	}
}