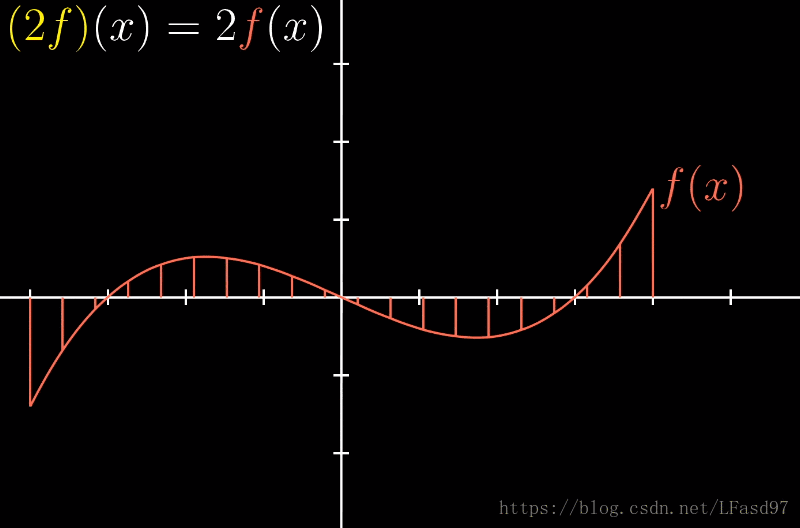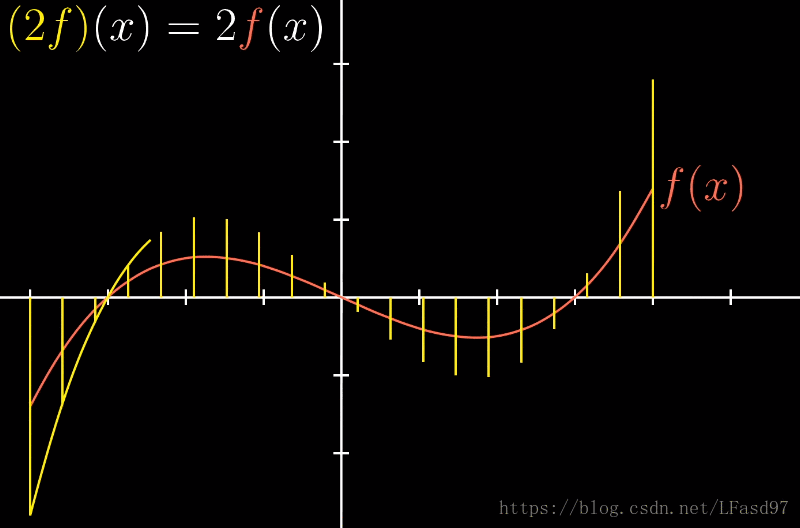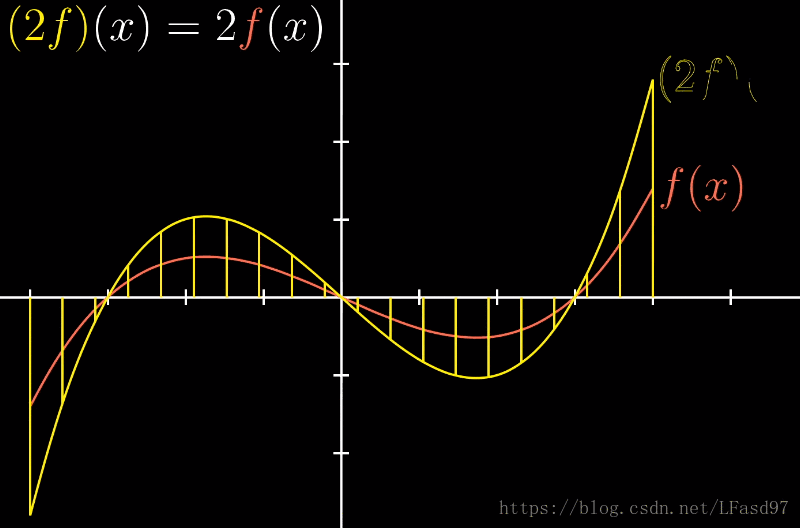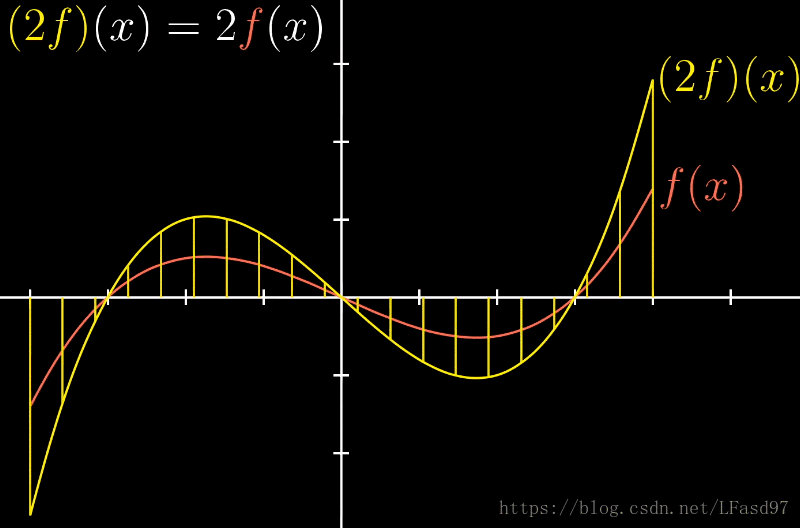线性代数的本质（十）——抽象向量空间

我们现在重新看第一节一个看似简单的问题：“向量是什么”？以二维向量为例，它是一个箭头，为了方便我们使用坐标来描述它？或者它是本身就是一个实数对，我们只是将它形象理解成空间的一个箭头？还是说这两种观点只是抽象事物的体现？

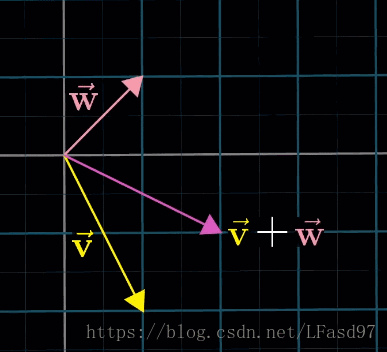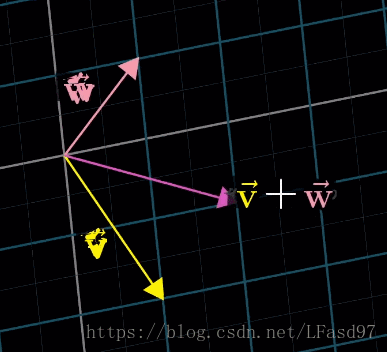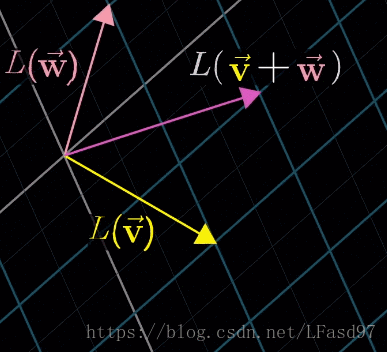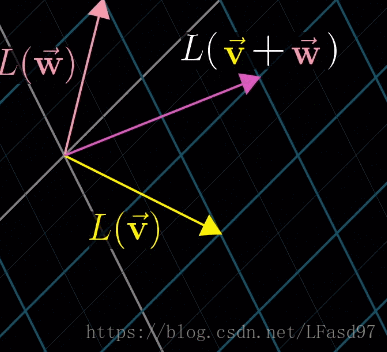
从某种意义上讲，函数实际上就是另一种向量。类比两个向量的加法，我们也可以将两个函数 $f$ 和 $g$ 相加从而获得一个新的函数 $(f+g)$

类似的，函数的数乘跟向量数乘类似

函数的线性变换也是一样，这个变换接收一个函数，然后把它变成另一个函数。在为几分钟我们可以找到一个常见的例子——导数。回顾第三节，我们知道一个变换是线性的主要看这个变换满不满足可加性和成比例这两个基本特性。

$L(v+w)=L(v)+L(w)$

$L(cv)=cL(v)$

学过求导的人知道，求导符合变换的可加性和成比例，所以求导是线性运算。

$\frac{d}{dx}(x^3+x^2)=\frac{d}{dx}(x^3)+\frac{d}{dx}(x^2)$

$\frac{d}{dx}(4x^3)=4\frac{d}{dx}(x^3)$

我们看看怎么用矩阵来描述求导。我们现在把目光限制在多项式空间中，这个空间有无穷个基函数，分别是 $x$ 的不同次幂。

$$\begin{gathered} b_0(x)=1 \\ {b}_1(x)=x \\ {b}_2(x)=x^2 \\ ... \end{gathered}$$

这里基函数的作用就跟我们之前用到的 $\hat{i}$，$\hat{j}$，$\hat{k}$ 的作用类似，因为多项式的次数没有限制，所以这个空间的基函数有无穷个。在这个向量空间中我们可以这样来描述 $x^2+3x+5$，$\left[\begin{array}{c}5\\ 3\\ 1\\ ...\end{array}\right]$，在这个坐标系中，求导是用一个无穷阶的矩阵来描述的 $\left[\begin{array}{ccccc}0& 1& 0& 0& ...\\ 0& 0& 2& 0& ...\\ 0& 0& 0& 3& ...\\ 0& 0& 0& 0& ...\\ ...& ...& ...& ...& ...\end{array}\right]$

我们使用这个矩阵来计算 $\frac{d}{dx}(x^3+5x^2+4x+5)$

把 $\frac{d}{dx}(x^3+5x^2+4x+5)$ 用向量描述 $\left[\begin{array}{c}5\\ 4\\ 5\\ 1\\ ...\end{array}\right]$ 然后计算矩阵向量数乘

$\left[\begin{array}{ccccc}0& 1& 0& 0& ...\\ 0& 0& 2& 0& ...\\ 0& 0& 0& 3& ...\\ 0& 0& 0& 0& ...\\ ...& ...& ...& ...& ...\end{array}\right]\left[\begin{array}{c}5\\ 4\\ 5\\ 1\\ ...\end{array}\right]=\left[\begin{array}{c}4\\ 10\\ 3\\ 0\\ ...\end{array}\right]$

把结果 $\left[\begin{array}{c}4\\ 10\\ 3\\ 0\\ ...\end{array}\right]$ 转换成用函数多项式来表示 $3x^2+10x+4$，的确就是 $\frac{d}{dx}(x^3+5x^2+4x+5)$ 的结果。

至于这里代表求导的矩阵的构造方式跟前面所讲的矩阵一样，用变换后的基向量组合成矩阵，由于这里的变换代表求导，所以变换后的基向量就是基函数求导后的结果

$\frac{d}{dx}{b}_0(x)=\frac{d}{dx}(1)=0=\left[\begin{array}{c}0\\ 0\\ 0\\ ...\end{array}\right]$

$\frac{d}{dx}{b}_1(x)=\frac{d}{dx}(x)=1=\left[\begin{array}{c}1\\ 0\\ 0\\ ...\end{array}\right]$

$\frac{d}{dx}{b}_2(x)=\frac{d}{dx}(x^2)=2x=\left[\begin{array}{c}0\\ 2\\ 0\\ ...\end{array}\right]$

$\frac{d}{dx}{b}_3(x)=\frac{d}{dx}(x^3)=3x^2=\left[\begin{array}{c}0\\ 0\\ 3\\ ...\end{array}\right]$

咋一看，矩阵向量乘法跟函数求导没有什么关系，但他们其实是一家人，也更好的说明了函数是向量的一种体现。回到这节一开始提到的问题中来，“向量是什么”，我们可以说有很多类似向量的事物，这些对象拥有合理的数乘和相加的概念那么线性代数中所有关于向量、线性变换和其他概念都应该适用于它。为了使线性代数的定义和定理不只对一个特殊情况适用，对其他类似向量的事物 都具有普适性。所以数学家并没有明确定义向量是什么东西，而是建立一系列向量加法和数乘必须遵守的规则，在线性代数的现代理论中如果要让所有已经借利好的理论和概念适用于一个向量空间，那么它必须满足八条公理。

这些公理作为一种媒介联系着数学家和将线性代数的结论应用于新向量空间的人。对于我们这些需要使用线性代数的人，在使用结论前只要保证对象满足上面的规则就行了，而数学家就可以不用考虑使用者所定义的千奇百怪的向量空间。所以，向量的形式并不重要，只要向量的相加和数乘满足上面八个定理，那么我们前面讲到的线性变换，行列式，特征向量等等结论都能成立。就像一个数字3，在遇到具体情况的时候，代表三个东西的集合，但是在数学中被看作所有三个东西的集合的抽象概念，从而能让你通过一个概念来推出所有三个东西的集合。向量也是如此，它有很多种体现，但是数学把它抽象成“向量空间”这样一个无形的概念。

线性代数本身是一门数学，讨论的主要通过代数计算的方法来解决线性问题，就跟笛卡尔发明了解析几何一样，通过代数解决几何问题。在后面的学习工作中，希望大家能够善用线性代数这门工具。