左偏树（可并堆）

“左偏”树？

左偏树其实是一种可并堆，它可以 O(log2n) O ( l o g 2 n ) 合并两个堆。

那左偏？也就是说他左边肯定有什么东西比右边大……

别着急，在左偏树上有一个叫距离的东西：

个点的距离，被定义为它子树中离他最近的外节点到这个节点的距离（这与树的深度不同）

其中我们定义一个节点为外节点，当且仅当这个节点的左子树和右子树中的一个是空节点。（注意外节点不是叶子节点）

这幅图中的这三个节点都是外节点。

而左偏树指的就是就是一个节点的左儿子的距离一定大于等于右儿子的距离。

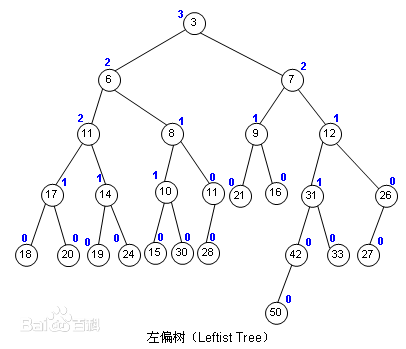
例如下面就是一棵左偏树（蓝色数字表示每个节点的距离）

它有什么特别的吗？

一个合格的左偏树，满足下列性质：

1. 左偏树中任意一个节点的距离为其右儿子的距离 +1 + 1
   disti=distrsoni+1 d i s t i = d i s t r s o n i + 1 （显然）

2. n n 个点的左偏树，距离最大为 log(n+1)−1 l o g ( n + 1 ) − 1
   证明还是很简单的，考虑左偏树根节点的距离 d d 为一定值，那么节点数最少的情况就是一个完全二叉树，节点数为 2d+1−1 2 d + 1 − 1 。那么n个节点的左偏树距离也就 ≤log(n+1)−1 ≤ l o g ( n + 1 ) − 1 。

怎么用它？

merge：

既然是可并堆肯定要合并啊！

现在有两棵左偏树， a,b a , b 是他们的根节点，假设 vala≤valb v a l a ≤ v a l b （否则 swap s w a p 一下 a,b a , b ）

既然 vala≤valb v a l a ≤ v a l b ，说明如果将这两棵树合并，根应该还是 a a 。

这时，只需要递归合并 rsa,b r s a , b 这两个点，知道右儿子为空，并将新树的根节点作为 rsa r s a 。

合并完成之后， distrsa d i s t r s a 可能会变，为了保证左偏性质，如果 distlsa<distrsa d i s t l s a < d i s t r s a ，就交换 a a 的左右儿子。

最后，更新 dista d i s t a ，以 a a 为合并后的树的根节点。

代码实现：

int merge(int x,int y){
    if(x==0||y==0)return x|y;
    if(v[x].val>v[y].val||(v[x].val==v[y].val&&x>y))
        swap(x,y);
    v[x].lch=merge(v[x].lch,y);
    if(v[v[x].lch].disreturn v[x].dis=v[v[x].rch].dis+1,x;
}

这个合并和距离有关，所以是 O(log2n) O ( l o g 2 n )

push：

相当于与一个大小为1的堆合并。

pop：

相当于将根删除，然后左右儿子合并。

CODE模板：

洛谷 P3377 【模板】左偏树（可并堆）

#include
#include
using namespace std;

#define lch ch[0]
#define rch ch[1]
int n,m,x,y,opt;
struct Leftist{
    int val,dis,fa,ch[2];
    friend int find(int x);
    friend int merge(int x,int y);
    inline int top();
    inline void pop();
}v[1000005];

int find(int x){
    while(v[x].fa)x=v[x].fa;
    return x;
}

int merge(int x,int y){
    if(x==0||y==0)return x|y;
    if(v[x].val>v[y].val||(v[x].val==v[y].val&&x>y))
        swap(x,y);
    v[x].lch=merge(v[x].lch,y);
    v[v[x].lch].fa=x;
    if(v[v[x].lch].disreturn v[x].dis=v[v[x].rch].dis+1,x;
}

inline int Leftist::top(){return val;}

inline void Leftist::pop(){
    val=-1;
    v[lch].fa=v[rch].fa=0;
    merge(lch,rch);
}

int main(){
    scanf("%d%d",&n,&m);
    v[0].dis=-1;
    for(int i=1;i<=n;i++)scanf("%d",&v[i].val);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&opt,&x);
        if(opt==1){
            scanf("%d",&y);
            if(~v[x].val&&~v[y].val&&x!=y){
                int fx=find(x),fy=find(y);
                merge(fx,fy);
            }
        }else{
            if(v[x].val==-1)puts("-1");
            else{
                int fx=find(x);
                printf("%d\n",v[fx].top());
                v[fx].pop();
            }
        }
    }
}