Code92007
Code92007

牛客小白月赛9 A-签到(逆元性质)

题目链接

https://ac.nowcoder.com/acm/contest/275/A

思路来源

https://ac.nowcoder.com/acm/contest/view-submission?submissionId=37485613

心得

get到了逆元的性质，

比如说每次乘以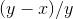(y-x)/y的时候，直接乘以mod意义下的(y-x)*y^{_-1}

而假设最后求的分数是\frac{p}{q}，即p*q^{-1}时，

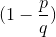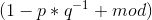此时要求(1-\frac{p}{q})，只需(1-p*q^{-1}+mod)%mod即可，

也就是说，逆元世界里，没有分母，剩下的可以统一过来。

 

顺便在这里写下，阶乘逆元的性质

由n!=(n-1)!*n，

则由inv(n!)=inv((n-1)!)*inv(n),

两侧同乘1/inv(n)，即同乘inv(inv(n))=n知，

inv(n!)*n=inv((n-1)!)

因此，可利用inv(n)求inv(n-1)，先求得inv(maxn)后，

可预处理出阶乘逆元表，O(n)

 

牛客小白月赛9 A-签到(逆元性质)_第1张图片

当然用inv[i]=(mod-mod/i)*inv[mod%i]%mod（记忆化O(logn)搜索）也可，注意i

牛客小白月赛9 A-签到(逆元性质)_第2张图片

求出每个的逆元之后阶乘一下。

 

代码

#include 
#include  
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
const long long int INF=1e18;
const int maxn=1e5+10; 
const int mod=1e9+7;
const int MOD=998244353;
const double eps=1e-9;
typedef long long ll;
#define vi vector 
#define si set
#define pii pair 
#define pi acos(-1.0)
#define pb push_back
#define mp make_pair
#define lowbit(x) (x&(-x))
#define sci(x) scanf("%d",&(x))
#define scll(x) scanf("%lld",&(x))
#define sclf(x) scanf("%lf",&(x))
#define pri(x) printf("%d",(x))
#define rep(i,j,k) for(int i=j;i<=k;++i)
#define per(i,j,k) for(int i=j;i>=k;--i)
#define mem(a,b) memset(a,b,sizeof(a)) 
using namespace std;
int n;
ll ans;
ll modpow(ll x,ll n,ll mod)
{
    ll res=1;
    while(n)
    {
        if(n&1)res=res*x;
        if(res>mod)res%=mod;
        x*=x;
        if(x>mod)x%=mod;
        n/=2;
    }
    return res;
}
int main()
{
	ans=1;
    sci(n);
    rep(i,0,n-1)
    {
    	int a,b;
    	sci(a),sci(b);
    	ans*=(b-a)*modpow(b,mod-2,mod)%mod;
    	if(ans>mod)ans%=mod;
    }
    printf("%lld\n",(1-ans+mod)%mod);
    return 0;
}

 

你可能感兴趣的:(数论)

  • lisp不是函授型语言_LISP语言 sunlee0520 lisp不是函授型语言
    [拼音]：LISPyuyan[外文]：LISP为非数值符号运算而设计的表处理语言。LISP是英文LISTPROCESSING(表处理)的缩写。LISP语言是1960年J.麦卡锡在递归函数论基础上首先设计出来的。LISP语言的形式化程度高，表达力强，适合于描述各种知识和编写问题求解的程序，因此一直是用来研究人工智能的一种基本语言。自然语言中词可以认为是能单独用来构成句子的最小单元，由词可以构成词组，
  • 数论问题61一一各种进位制 李扩继 深度学习数学建模大数据学习方法算法
    10进位制是普遍使用的数进位制，二进位制是计算机采用的进位制。还有三进位制，四进位制，…等等。那一种进位制都能转化为10进位制。下面介绍这种方法。①10进位制的表示(口诀:逢10进1)如8X1000+7X100+5x10+3=8753。②2进位制的表示(口诀:逢2进1)如2进位制数101101(2)转化为10进制101101=1x2^5+0x2^4+1x2^3+1x2^2+0x2+1=32+8+4
  • 求质因数个数 程序猿小假 算法
    什么是质因数？质因数：在数论里是指能整除给定正整数的质数。也就是说，如果一个质数是某个数的因数，那么这个质数就是这个数的质因数。例如，对于数字12，它的因数有1、2、3、4、6、12。其中2和3是质数，所以12的质因数是2和3。如何求一个数有多少个质因数呢？举一个例子，方便大家理解~例：求2024有几个质因数？1.从最小的质数开始尝试分解最小的质数是2，我们先看2024能否被2整除。2024/2=
  • 计算机密码体制分为哪两类,密码体制的分类.ppt 约会师老马 计算机密码体制分为哪两类
    密码体制的分类.ppt密码学基本理论现代密码学起始于20世纪50年代，1949年Shannon的《TheCommunicationTheoryofSecretSystems》奠定了现代密码学的数学理论基础。密码体制分类(1)换位与代替密码体制序列与分组密码体制对称与非对称密钥密码体制数学理论数论信息论复杂度理论数论--数学皇后素数互素模运算，模逆元同余方程组，孙子问题，中国剩余定理因子分解素数梅森
  • 致良知之寄诸用明书 BonSun
    众所周知，当今社会，父母和社会、学校对学生的期望往往是唯分数论，包括每个人对成功的理解也往往是功名利禄，忽视了最基本的学问。文中提到，花之千叶者无实，为其华美太发露耳。人只有沉下心来，韬光养晦，才能拥有真正的学问和本领。
  • Python【math数学函数】 Alan_Lowe #Pythonpython
    Python【math数学函数】文章目录Python【math数学函数】数论与表示函数1.ceil()和floor()2.comb()3.copysign()4.fabs()5.factorial()6.gcd()7.lcm()幂函数与对数函数1.exp()和math.e和pow()2.log()和log2()和log10()3.sqrt(x)三角函数1.asin、acos()、atan()2.s
  • python 实现eulers totient欧拉方程算法 luthane 算法python开发语言
    eulerstotient欧拉方程算法介绍欧拉函数（Euler’sTotientFunction），通常表示为()，是一个与正整数相关的函数，它表示小于或等于的正整数中与互质的数的数目。欧拉函数在数论和密码学中有广泛的应用。欧拉函数的性质1.**对于质数，有φ(p)=p−1∗∗φ(p)=p−1^{**}φ(p)=p−1∗∗。2.**如果是质数的次幂，即n=pkn=p^kn=pk，则φ(n)=pk−
  • 算法设计与分析学习（6）——数论 罗塞菈桔梨萝柚 算法学习算法线性代数
    数论整除基本概念若aaa和bbb为整数，且a≠0a≠0a=0若存在整数qqq使得b=aqb=aqb=aq，那么就说aaa可以整除bbb或是bbb被aaa整除，记作a∣ba|ba∣b。aaa也被称为bbb的约数，bbb也被称为a的倍数。若bbb不能被aaa整除，则记作a∤ba\not{|}ba∣b。整数p≠0,±1p≠0,±1p=0,±1，且除了±1,±p±1,±p±1,±p外没有其他的约数
  • 数论——欧几里得算法 NarutoTime 数论算法c++数据结构c语言
    1.欧几里得简介    欧几里得（希腊文：Ευκλειδης，约公元前330年—公元前275年），古希腊数学家，被称为“几何之父”。他最著名的著作《几何原本》是欧洲数学的基础，在书中他提出五大公设。欧几里得的《几何原本》被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。2.欧几里得算法欧几里得算法用于：求解a和b的最大公约数。最大公约数英文为：Gre
  • 数论——扩展欧几里得算法 NOI_yzk
    欧几里得&拓展欧几里得（Euclid&Extend-Euclid）欧几里得算法（Euclid）背景：欧几里德算法又称辗转相除法，用于计算两个正整数a，b的最大公约数。——百度百科代码：递推的代码是相当的简洁：intgcd(inta,intb){returnb==0?a:gcd(b,a%b);}分析：方法说了是辗转相除法，自然没有什么好介绍的了。。Fresh肯定会觉得这样递归下去会不会爆栈？实际上在
  • 数论学习1（欧几里德算法+唯一分解定理+埃氏筛+拓展欧几里德+同余与模算术） new出新对象！ 数学数算法学习
    目录1.唯一分解定理2.欧几里德算法（求最大公约数）3.求最小公倍数4.埃氏筛5.拓展欧几里德算法(1)证明一下线性方程组的正数的最小值是多少，(2)如何通过裴蜀定理退出拓展欧几里得算法(贝祖定理)6.同余与模算术(1)取模运算操作加法取模运算减法取模运算乘法取模运算(2)特殊的取模操作大整数取模幂取模(3)同余式，乘法逆元，费马小定理今天也是小小的开始学习数论方面的知识了，首先数论的入门章节必然
  • Collatz 猜想和 Python 不连续小姐
    PythonDay4:CollatzConjecture原来总有学生问我，微积分有什么用啊，我说如果微积分学好了，也许抽象代数和数论就能学好，那最后就能像AndrewWiles一样上人物年度杂志的封面了.(AndrewWiles证明了Fermat'sLastTheorem，费玛大定理).[captionid="attachment_1466"align="alignnone"width="300"
  • 初等数论--整除--带余除法 WeidanJi 初等数论数学密码学信息安全
    初等数论--整除--带余除法概念基本性质带余除法博主本人是初学初等数论（整除+同余+原根），本意是想整理一些较难理解的定理、算法，加深记忆也方便日后查找；如果有错，欢迎指正。我整理成一个系列：初等数论，方便检索。概念初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。b∣a:若a,b∈Z,b≠0，∃c∈Z,使a=bc,则称b整除a
  • 河南萌新2024第四场 Pown_ShanYu 算法数据结构
    C岗位分配题目大意：有n个岗位，m位志愿者，每个岗位至少需要a个志愿者，并且可以有志愿者可以空闲下来作预备，给出可能的分配情况总数思路：首先将每个岗位分配好至少需要的志愿者，再将剩下的人进行分配，那就满足球同盒不同模型（允许空盒），可用隔板法进行分配，需要额外开设一个空闲岗位用来预备，那么按照4个人去4个岗位，那么为c73，具体操作可看数论模板中发布的隔板法问题，递归求组合数Solved：intn
  • 【读书笔记】吴非《致青年教师》(4) 冬儿菇凉
    一、精要摘录(48——106页)1.教育教学不能“唯分数论“，比分数重要的是学生思维品质和解决实际问题的能力。2.一名教师心中有使命感，心中有学生才会很在意学生对他的态度，在意学生的接受度。3.作为教师，你要善于向学生问出有意思的问题。4.教育就是要培养好习惯，教是为了达到不需要教学生，不需要老师教了是教学的成功，也是教师的职业追求。5.教师是学习者，在学习上教师首先要郑重其事，学生才有可能养成敬
  • 【代码随想录算法训练营Day39】62.不同路径；63. 不同路径 II 想做一只潜水的猪 算法
    文章目录❇️Day39第九章动态规划part02✴️今日任务❇️62.不同路径自己的思路自己的代码随想录思路随想录代码❇️63.不同路径II自己的思路自己的代码随想录代码❇️Day39第九章动态规划part02✴️今日任务今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径63.不同路径II❇️62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难
  • 算法D39 | 动态规划2 | 62.不同路径 63. 不同路径 II memolaner 算法训练营算法动态规划数据结构c++python
    今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难想到。代码随想录视频讲解：动态规划中如何初始化很重要！|LeetCode：62.不同路径_哔哩哔哩_bilibili这个题看到路径的表示，第一直觉就是一个组合数的问题，学了一下C++计算组合数防止溢出的小技巧。第二个方法再动态规划完成，重点是把二维的动态规划
  • 牛客周赛 Round 35（A,B,C,D,E,F,G） 邪神与厨二病 牛客算法暴力c++数论滑动窗口单调队列贪心构造
    这场简单，甚至赛时90分钟不到就AK了。比赛链接，队友题解友链刚入住学校监狱，很不适应，最近难受的要死，加上最近几场CF打的都不顺利，san值要爆掉了，只能慢慢补题了。这场C是个滑动窗口，D是贪心，E是有点麻烦的构造，FG是数论。A小红的字符串切割思路：记录一下字符串长度，然后从中间拆开。code：#include#include#includeusingnamespacestd;strings;
  • 算法——数论——同余 戏拈秃笔 数据结构与算法（java版）算法
    目录同余一、试题算法训练同余方程同余同余使人们能够用等式的形式简洁地描述整除关系同余：若m（正整数），a和b是整数，a%m==b%m，或(a-b)%m==0，记为ab(modm)求解一元线性同余方程等价于求解二元线性丢番图方程一元线性同余方程，解法看下面第一题二元线性丢番图方程逆：的一个解为a模m的逆一、试题算法训练同余方程问题描述求关于x的同余方程ax≡1(modb)的最小正整数解。输入格式输入
  • pku acm 题目分类 moxiaomomo 算法数据结构numbers优化calendarcombinations
    1.搜索//回溯2.DP（动态规划）3.贪心北大ACM题分类2009-01-2714.图论//Dijkstra、最小生成树、网络流5.数论//解模线性方程6.计算几何//凸壳、同等安置矩形的并的面积与周长sp;7.组合数学//Polya定理8.模拟9.数据结构//并查集、堆sp;10.博弈论1、排序sp;1423,1694,1723,1727,1763,1788,1828,1838,1840,22
  • C++STL之Queue容器 芯片烧毁大师 数据结构C++c++开发语言
    C++STL之Queue容器1.再谈队列回顾一下之前所学的队列，队列和栈不同，队列是一种先进先出的数据结构，STL的队列内容极其重要，虽然内容较少但是请务必掌握，STL的队列是快速构建搜索算法以及相关的数论图论的状态存储的基础。2.相关头文件头文件：#include3.初始化格式为：**explicit**queue(**const**container_type&ctnr=container_t
  • 数字签名算法MD5withRSA Just_Paranoid 技术流Clipmd5rsasignatrue
    数字签名MD5withRSA，：将正文通过MD5数字摘要后，将密文再次通过生成的RSA密钥加密，生成数字签名，将明文与密文以及公钥发送给对方，对方拿到私钥/公钥对数字签名进行解密，然后解密后的，与明文经过MD5加密进行比较，如果一致则通过使用Signature的API来实现MD5withRSARSA原理：RSA算法基于一个十分简单的数论事实，将两个大素数相乘十分容易，但反过来想要对其乘积进行因式分
  • 2301: 不定方程解的个数 jht0105 算法
    题目描述输出不定方程解的个数。在数学中，不定方程是数论中的一个重要课题，在各种比赛中也常常出现.对于不定方程，有时我们往往只求非负整数解，现有方程ax+by+c=0，其中x、y为未知量且不超过10000，当给定a、b、c的值以后，可求出n组x、y的非负整数解，n>=0，,其中a，b，c均为[-10000,10000].输入描述一行，三个空格隔开的整数，为a、b、c的值。输出描述一个整数，为合法的解
  • python伯努利多项式 微小冷 #sympypython开发语言sympy伯努利数排列组合符号计算
    文章目录伯努利数和多项式sympy实现伯努利数是一种在数学、物理和工程中广泛应用的特殊数列，以瑞士数学家雅各布·伯努利（JacobBernoulli）的名字命名，并在许多领域中发挥重要作用。在数学中，它们与斐波那契数列、卡塔兰数、贝尔数等数列有密切联系，可以用于解决循环问题、组合问题和递推关系等数学问题。伯努利数和多项式伯努利(Bernoulli)数是一组在数论和复分析中出现的数，与伯努利多项式有
  • 二次剩余问题x的求解及代码实现（python） JustGo12 数论安全1024程序员节
    一、问题引入二次剩余是数论基本概念之一。它是初等数论中非常重要的结果，不仅可用来判断二次同余式是否有解，还有很多用途。C.F.高斯称它为算术中的宝石，他一人先后给出多个证明。[1]研究二次剩余的理论称为二次剩余理论。二次剩余理论在实际上有广泛的应用，包括从噪音工程学到密码学以及大数分解。即关于方x^2≡a(modp)对于这个方程，求出满足条件的x。二、x的求解在上述问题下，根据p值的不同性质，可以
  • 【数论】exgcd 扩展欧几里得算法 Texcavator 数论算法
    参考：exgcd详解-zzt1208-博客园(cnblogs.com)exgcd（扩展欧几里得算法），用来求形如ax+by=gcd(a,b)ax+by=gcd(a,b)ax+by=gcd(a,b)（a,ba,ba,b为常数）的方程的一组整数解。（如果不确定等号右边是不是gcd，可以先当做gcd，求出来之后验证，是的话就是解，不是的话就不是解）推导见上面的链接，这篇只放个板子codeintexgcd
  • 2021-07-30 RX-0493
    学了一会数论，好难1.乘法逆元：a/b%p,若a/b在进行取模运算时，会出现精度问题，而且模运算对除法不适用，（没有分配律，大概就这意思）而求出乘法逆元后，可以把原式变为a*x%p的形式，且值不变。a*x≡1（modp）中，a,p为已知量，则x为a的乘法逆元。例题：乘法逆元设p=k*i+r,(1usingnamespacestd;constintN=20000530;intn,p,inv[N];i
  • 同余数论性质 clmm_ 算法
    同余概念当a%m==b%m，说明a和b同余，写作若a≡b(modm)性质衍生出几条性质1.m|abs(a-b)，即|a-b|是m的倍数。（注意，0是任何数的倍数）2.当a≡b(modm)，c≡d(modm)，有ac≡bd(modm)有a+c≡b+d(modm)有a-c≡b-d(modm)证明如下
  • 读《爱心与教育》第八天 皮_小皮
    作为一名教师，尤其是班主任老师，“培优转差”是教育工作的一项重要内容，读了李镇西老师的《爱心与教育》，自己受到不小的启发，对“优生”的培养和后进生的转化有了新的认识和思考。对“优生”的重新认识——李老师说：“优生”当然应该是指品学兼优的学生，但在现在不少教师、家长的眼中，所谓“优生”更多的是指学习成绩拔尖的学生（即尖子生）。的确，在升学竞争和应试教育的大环境下，很多教育者都以分数论英雄，对“优生”
  • RSA算法 superdont 图像加密算法java服务器
    RSA算法是一个非对称加密算法，它依赖于数论中的大整数因数分解问题的困难性。在RSA中，加密和解密使用不同的密钥，分别称为公钥和私钥。RSA算法的基本原理包括以下几个步骤：密钥生成：a.选择两个大的质数(p)和(q)。b.计算它们的乘积(n=pq)，n的长度就是密钥长度。c.计算欧拉函数(\phi(n)=(p-1)(q-1))。d.选择一个整数(e)，使得(1
  • jQuery 跨域访问的三种方式 No 'Access-Control-Allow-Origin' header is present on the reque qiaolevip 每天进步一点点学习永无止境跨域众观千象
    XMLHttpRequest cannot load http://v.xxx.com. No 'Access-Control-Allow-Origin' header is present on the requested resource. Origin 'http://localhost:63342' is therefore not allowed access. test.html:1
  • mysql 分区查询优化 annan211 java分区优化mysql
    分区查询优化 引入分区可以给查询带来一定的优势，但同时也会引入一些bug. 分区最大的优点就是优化器可以根据分区函数来过滤掉一些分区，通过分区过滤可以让查询扫描更少的数据。 所以，对于访问分区表来说，很重要的一点是要在where 条件中带入分区，让优化器过滤掉无需访问的分区。 可以通过查看explain执行计划，是否携带 partitions
  • MYSQL存储过程中使用游标 chicony Mysql存储过程
    DELIMITER $$ DROP PROCEDURE IF EXISTS getUserInfo $$ CREATE PROCEDURE getUserInfo(in date_day datetime)-- -- 实例-- 存储过程名为：getUserInfo-- 参数为：date_day日期格式:2008-03-08--    BEGINdecla
  • mysql 和 sqlite 区别 Array_06 sqlite
    转载： http://www.cnblogs.com/ygm900/p/3460663.html mysql 和 sqlite 区别 SQLITE是单机数据库。功能简约，小型化，追求最大磁盘效率 MYSQL是完善的服务器数据库。功能全面，综合化，追求最大并发效率 MYSQL、Sybase、Oracle等这些都是试用于服务器数据量大功能多需要安装，例如网站访问量比较大的。而sq
  • pinyin4j使用 oloz pinyin4j
    首先需要pinyin4j的jar包支持；jar包已上传至附件内 方法一:把汉字转换为拼音；例如：编程转换后则为biancheng      /** * 将汉字转换为全拼 * @param src 你的需要转换的汉字 * @param isUPPERCASE 是否转换为大写的拼音； true:转换为大写；fal
  • 微博发送私信 随意而生 微博
    在前面文章中说了如和获取登陆时候所需要的cookie，现在只要拿到最后登陆所需要的cookie，然后抓包分析一下微博私信发送界面 http://weibo.com/message/history?uid=****&name=**** 可以发现其发送提交的Post请求和其中的数据， 让后用程序模拟发送POST请求中的数据，带着cookie发送到私信的接入口，就可以实现发私信的功能了。
  • jsp 香水浓 jsp
    JSP初始化     容器载入JSP文件后，它会在为请求提供任何服务前调用jspInit()方法。如果您需要执行自定义的JSP初始化任务，复写jspInit()方法就行了 JSP执行     这一阶段描述了JSP生命周期中一切与请求相关的交互行为，直到被销毁。     当JSP网页完成初始化后
  • 在 Windows 上安装 SVN Subversion 服务端 AdyZhang SVN
    在 Windows 上安装 SVN Subversion 服务端2009-09-16高宏伟哈尔滨市道里区通达街291号   最佳阅读效果请访问原地址：http://blog.donews.com/dukejoe/archive/2009/09/16/1560917.aspx   现在的Subversion已经足够稳定，而且已经进入了它的黄金时段。我们看到大量的项目都在使
  • android开发中如何使用 alertDialog从listView中删除数据？ aijuans android
    我现在使用listView展示了很多的配置信息，我现在想在点击其中一条的时候填出 alertDialog,点击确认后就删除该条数据，（ ArrayAdapter ，ArrayList，listView 全部删除），我知道在 下面的onItemLongClick 方法中 参数 arg2  是选中的序号，但是我不知道如何继续处理下去 1 2 3
  • jdk-6u26-linux-x64.bin 安装 baalwolf linux
    1.上传安装文件(jdk-6u26-linux-x64.bin) 2.修改权限 [root@localhost ~]# ls -l /usr/local/jdk-6u26-linux-x64.bin 3.执行安装文件 [root@localhost ~]# cd /usr/local [root@localhost local]# ./jdk-6u26-linux-x64.bin&nbs
  • MongoDB经典面试题集锦 BigBird2012 mongodb
    1.什么是NoSQL数据库？NoSQL和RDBMS有什么区别？在哪些情况下使用和不使用NoSQL数据库？ NoSQL是非关系型数据库，NoSQL = Not Only SQL。 关系型数据库采用的结构化的数据，NoSQL采用的是键值对的方式存储数据。 在处理非结构化/半结构化的大数据时；在水平方向上进行扩展时；随时应对动态增加的数据项时可以优先考虑使用NoSQL数据库。 在考虑数据库的成熟
  • JavaScript异步编程Promise模式的6个特性 bijian1013 JavaScriptPromise
            Promise是一个非常有价值的构造器，能够帮助你避免使用镶套匿名方法，而使用更具有可读性的方式组装异步代码。这里我们将介绍6个最简单的特性。         在我们开始正式介绍之前，我们想看看Javascript Promise的样子： var p = new Promise(function(r
  • [Zookeeper学习笔记之八]Zookeeper源代码分析之Zookeeper.ZKWatchManager bit1129 zookeeper
    ClientWatchManager接口 //接口的唯一方法materialize用于确定那些Watcher需要被通知 //确定Watcher需要三方面的因素1.事件状态 2.事件类型 3.znode的path public interface ClientWatchManager { /** * Return a set of watchers that should
  • 【Scala十五】Scala核心九：隐式转换之二 bit1129 scala
    隐式转换存在的必要性，   在Java Swing中，按钮点击事件的处理，转换为Scala的的写法如下：   val button = new JButton button.addActionListener( new ActionListener { def actionPerformed(event: ActionEvent) {
  • Android JSON数据的解析与封装小Demo ronin47
    转自：http://www.open-open.com/lib/view/open1420529336406.html package com.example.jsondemo; import org.json.JSONArray; import org.json.JSONException; import org.json.JSONObject;    impor
  • [设计]字体创意设计方法谈 brotherlamp UIui自学ui视频ui教程ui资料
      从古至今，文字在我们的生活中是必不可少的事物，我们不能想象没有文字的世界将会是怎样。在平面设计中，UI设计师在文字上所花的心思和功夫最多，因为文字能直观地表达UI设计师所的意念。在文字上的创造设计，直接反映出平面作品的主题。 如设计一幅戴尔笔记本电脑的广告海报，假设海报上没有出现“戴尔”两个文字，即使放上所有戴尔笔记本电脑的图片都不能让人们得知这些电脑是什么品牌。只要写上“戴尔笔
  • 单调队列-用一个长度为k的窗在整数数列上移动，求窗里面所包含的数的最大值 bylijinnan java算法面试题
    import java.util.LinkedList; /* 单调队列 滑动窗口 单调队列是这样的一个队列：队列里面的元素是有序的，是递增或者递减 题目：给定一个长度为N的整数数列a(i),i=0,1,...,N-1和窗长度k. 要求：f(i) = max{a(i-k+1),a(i-k+2),..., a(i)},i = 0,1,...,N-1 问题的另一种描述就
  • struts2处理一个form多个submit chiangfai struts2
    web应用中，为完成不同工作，一个jsp的form标签可能有多个submit。如下代码： <s:form action="submit" method="post" namespace="/my"> <s:textfield name="msg" label="叙述：">
  • shell查找上个月，陷阱及野路子 chenchao051 shell
    date -d "-1 month" +%F     以上这段代码，假如在2012/10/31执行，结果并不会出现你预计的9月份，而是会出现八月份，原因是10月份有31天，9月份30天，所以-1 month在10月份看来要减去31天，所以直接到了8月31日这天，这不靠谱。     野路子解决：假设当天日期大于15号
  • mysql导出数据中文乱码问题 daizj mysql中文乱码导数据
    解决mysql导入导出数据乱码问题方法： １、进入mysql，通过如下命令查看数据库编码方式： mysql>  show variables like 'character_set_%'; +--------------------------+----------------------------------------+ | Variable_name&nbs
  • SAE部署Smarty出现：Uncaught exception 'SmartyException' with message 'unable to write dcj3sjt126com PHPsmartysae
      对于SAE出现的问题：Uncaught exception 'SmartyException' with message 'unable to write file...。 官方给出了详细的FAQ：http://sae.sina.com.cn/?m=faqs&catId=11#show_213 解决方案为：   01 $path 
  • 《教父》系列台词 dcj3sjt126com
    Your love is also your weak point. 你的所爱同时也是你的弱点。   If anything in this life is certain, if history has taught us anything, it is that you can kill anyone.   不顾家的人永远不可能成为一个真正的男人。 &
  • mongodb安装与使用 dyy_gusi mongo
    一.MongoDB安装和启动,widndows和linux基本相同 1.下载数据库,     linux:mongodb-linux-x86_64-ubuntu1404-3.0.3.tgz 2.解压文件,并且放置到合适的位置     tar -vxf mongodb-linux-x86_64-ubun
  • Git排除目录 geeksun git
    在Git的版本控制中，可能有些文件是不需要加入控制的，那我们在提交代码时就需要忽略这些文件，下面讲讲应该怎么给Git配置一些忽略规则。   有三种方法可以忽略掉这些文件，这三种方法都能达到目的，只不过适用情景不一样。 1.  针对单一工程排除文件 这种方式会让这个工程的所有修改者在克隆代码的同时，也能克隆到过滤规则，而不用自己再写一份，这就能保证所有修改者应用的都是同一
  • Ubuntu 创建开机自启动脚本的方法 hongtoushizi ubuntu
    转载自： http://rongjih.blog.163.com/blog/static/33574461201111504843245/ Ubuntu 创建开机自启动脚本的步骤如下： 1) 将你的启动脚本复制到 /etc/init.d目录下 以下假设你的脚本文件名为 test。   2) 设置脚本文件的权限 $ sudo chmod 755
  • 第八章 流量复制/AB测试/协程 jinnianshilongnian nginxluacoroutine
    流量复制 在实际开发中经常涉及到项目的升级，而该升级不能简单的上线就完事了，需要验证该升级是否兼容老的上线，因此可能需要并行运行两个项目一段时间进行数据比对和校验，待没问题后再进行上线。这其实就需要进行流量复制，把流量复制到其他服务器上，一种方式是使用如tcpcopy引流；另外我们还可以使用nginx的HttpLuaModule模块中的ngx.location.capture_multi进行并发
  • 电商系统商品表设计 lkl
    DROP TABLE IF EXISTS `category`; -- 类目表 /*!40101 SET @saved_cs_client = @@character_set_client */; /*!40101 SET character_set_client = utf8 */; CREATE TABLE `category` ( `id` int(11) NOT NUL
  • 修改phpMyAdmin导入SQL文件的大小限制 pda158 sqlmysql
    　用phpMyAdmin导入mysql数据库时，我的10M的 数据库不能导入，提示mysql数据库最大只能导入2M。 　　 phpMyAdmin数据库导入出错： 　　You probably tried to upload too large file. Please refer to documentation for ways to workaround this limit.
  • Tomcat性能调优方案 Sobfist apachejvmtomcat应用服务器
    一、操作系统调优 对于操作系统优化来说，是尽可能的增大可使用的内存容量、提高CPU的频率，保证文件系统的读写速率等。经过压力测试验证，在并发连接很多的情况下，CPU的处理能力越强，系统运行速度越快。。 【适用场景】 任何项目。 二、Java虚拟机调优 应该选择SUN的JVM，在满足项目需要的前提下，尽量选用版本较高的JVM，一般来说高版本产品在速度和效率上比低版本会有改进。 J
  • SQLServer学习笔记 vipbooks 数据结构xml
    1、create database school 创建数据库school 2、drop database school 删除数据库school 3、use school 连接到school数据库，使其成为当前数据库 4、create table class(classID int primary key identity not null) 创建一个名为class的表，其有一
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他