【NOIP2017提高A组模拟8.24】提米树

Description：

1<=n<=100000

题解：

按dfs序dp。
设 fi 表示以dfs序中的第i个为叶子节点，能提供最多的决心。
盗一发题解图：

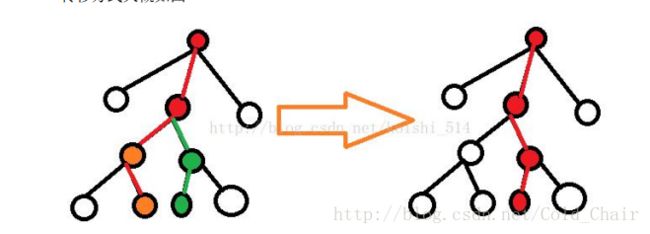
显然绿色节点会由橙色节点转移而来。
说具体的，就是dfs序上相邻的两个叶子节点x,y,y->lca路径上的点会由x->lca路径上的点转移而来。
暴力转移是 O(n2) 。
假设我们转移y->lca路径上的点时从上往下转移,那你发现x-Lca路径上的点的贡献变化是可以随便推推就维护的，维护个前缀后缀，随便搞搞就行了。

Code：

#include
#include
#define fo(i, x, y) for(int i = x; i <= y; i ++)
#define fd(i, x, y) for(int i = x; i >= y; i --)
#define max(a, b) ((a) > (b) ? (a) : (b))
using namespace std;

const int N = 100005;
int n, ans, a[N], d[N], t[N], dfn[N], dt, fa[N], f[N], g[N], h[N], ye[N], m[N], dep[N], bz[N];
int final[N], tot;
struct edge {
    int to, next;
}e[N];

void link(int x, int y) {
    e[++ tot].next = final[x], e[tot].to = y, final[x] = tot;
}

void dg(int x) {
    dfn[++ dt] = x;
    for(int i = final[x]; i; i = e[i].next)
        dep[e[i].to] = dep[x] + 1, dg(e[i].to), fa[e[i].to] = x;
}

void Init() {
    scanf("%d", &n);
    fo(i, 1, n) {
        scanf("%d", &a[i]);
        scanf("%d", &d[0]); ye[i] = d[0] == 0;
        fo(j, 1, d[0]) scanf("%d", &d[j]);
        fd(j, d[0], 1) link(i, d[j]);
    }
    dep[1] = 1; dg(1);
}

void Build(int i, int j) {
    d[0] = t[0] = 0;
    for(; dep[i] > dep[j]; i = fa[i]) d[++ d[0]] = i;
    for(; dep[i] < dep[j]; j = fa[j]) t[++ t[0]] = j;
    if(i == j) return;
    for(; i != j; i = fa[i], j = fa[j]) d[++ d[0]] = i, t[++ t[0]] = j;
}

void End() {
    int ii = 1; for(;!ye[dfn[ii]]; ii ++);
    while(1) {
        int jj = ii + 1;
        for(; jj <= n && !ye[dfn[jj]]; jj ++);
        if(jj > n) {
            int j = dfn[ii];
            while(j != 0) {
                if(!bz[j]) f[j] = a[j];
                ans = max(ans, f[j]);
                j = fa[j];
            }
            return;
        }
        Build(dfn[ii], dfn[jj]);
        fo(i, 1, t[0]) bz[t[i]] = 1;
        fo(i, 1, d[0]) if(!bz[d[i]]) f[d[i]] = a[d[i]], bz[d[i]] = 1;
        fo(i, 1, d[0] / 2) swap(d[i], d[d[0] - i + 1]);
        m[1] = -1e9; fo(i, 2, d[0]) m[i] = max(m[i - 1], a[d[i - 1]]);
        g[1] = f[d[1]]; fo(i, 2, d[0]) g[i] = max(g[i - 1], f[d[i]]);
        h[d[0]] = f[d[d[0]]] - m[d[0]]; fd(i, d[0] - 1, 1) h[i] = max(h[i + 1], f[d[i]] - m[i]);
        int z = 0, mx = -1e9; g[0] = -2e9; h[d[0] + 1] = -1e9;
        fd(i, t[0], 1) {
            int v = a[fa[t[i]]];
            if(v > mx) {
                while(z < d[0] && v > m[z + 1])
                    z ++;
                mx = v;
            }
            f[t[i]] = a[t[i]] + max(g[z] - mx, h[z + 1]);
        }
        ii = jj;
    }
}

int main() {
    Init();
    End();
    printf("%d", ans);
}