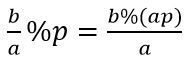乘法逆元

满足x与y的乘积对z取模等于1时，x和y对于模数z来说互为逆元
即 x*y=1(mod z)
为什么要求逆元呢？
比如求 (b/a)mod p 时，如果b大到不可直接求出，我们可以先求出在模数p下与a互为逆元的数x，那么 (b/a)mod p 转化成 (b*x)mod p

证明略。。。

求逆元：
方法一（a和p互质，扩展欧几里算法）：
：a * x + p * y = gcd( a , p )
等号两边同时对b取模：a * x % p = gcd( a , p )%p
当 gcd( a , p ) = 1 ，即a和p互质时：a * x % p = 1
得到了在模p下与a互为逆元的数x
注意：求出来x和p可能不同号，所以一定要判断并将x加p使之同号。！！！

x=(x%p+p)%p;

方法二（p是素数,费马小定理）：
a的逆元就是a的p-2次方

方法三：

方法四（p素数）：
O(p)求1~p内模p的所有逆元：

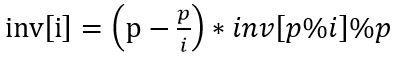
初始化 inv[1]=1，循环一遍即可求出所有逆元

方法五（阶乘的逆元）:
O(n)求1~n，所有数的阶乘的逆元
inv[ (n-1)! ] = inv[ n! ] * n
用以上方法求出 n! 的逆元之后，循环一遍即可求出其他阶乘的逆元

更多方法及证明见此处