计算机数据运算的那点儿事
数据上的运算可以分为三大类:算术运算、移位运算和逻辑运算。
逻辑运算
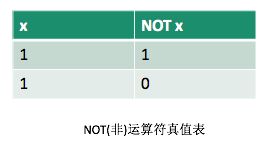
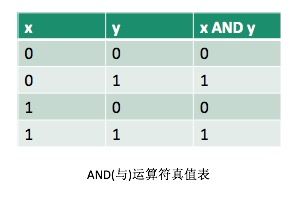
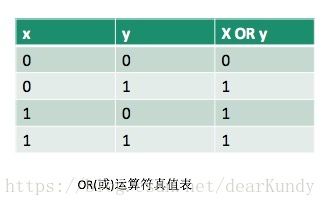
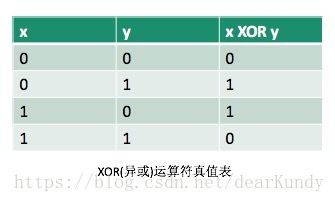
逻辑运算很简单,相应的位照着真值表来操作就可以。
移位运算
移位运算移动模式中的位,改变为的位置。它们能向左或向右移动位。我们可以吧移位运算分成两大类:逻辑移位运算和算术移位运算。
逻辑移位运算
逻辑移位运算应用于不带符号位的数的模式。原因是这些移位运算可能会改变数的符号。我们区分两类逻辑移位运算。
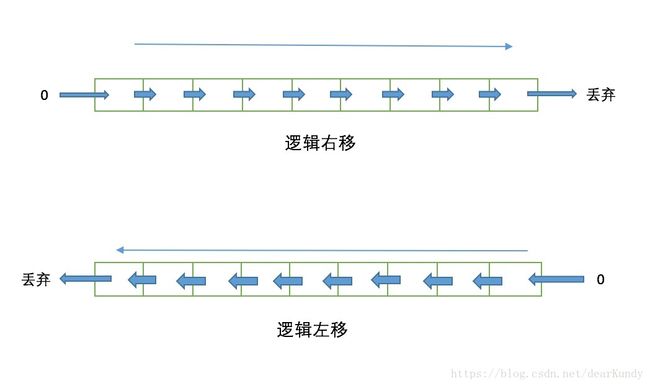
1.逻辑移位
逻辑右移运算把每一位向右移动一个位置。在n位模式中,最右位被丢弃,最左位填0。逻辑左移运算把每一位向左移动一个位置。在n位模式中,最左位被丢弃,最右位填0。
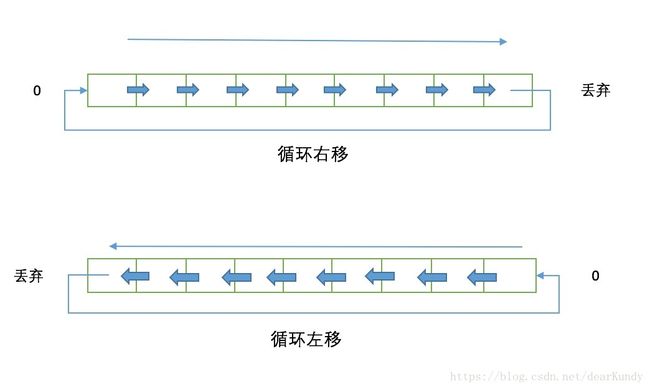
2.循环移位
循环移位运算(旋转运算)对位进行移动,但没有位被丢弃或增加。循环右移把每一位向右移动一个位置,最右位被回环,成为最左位。循环左移把每一位向左移动一个位置,最左位被回环,成为最右位。
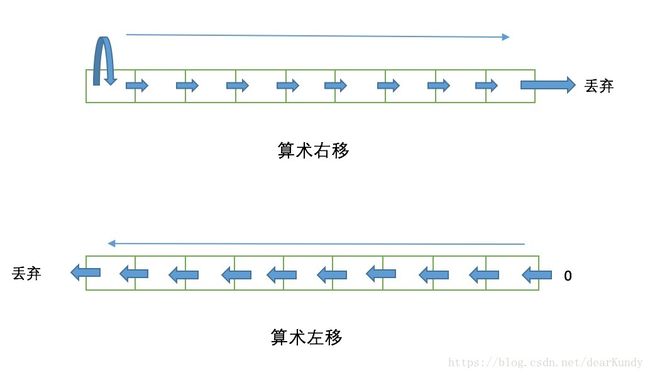
算术移位运算
算术移位运算假定位模式是用二进制补码格式表示的带符号的整数。算术右移被用来对整数除以2;而算术左移被用来对整数乘以2。这些运算不应该改变符号位。算术右移保留符号位,同时也把它复制,放入相邻的右边的位中,因此符号被保存。算术左移丢弃符号位,接收它的右边的位作为符号位。如果新的符号位与原先的相同,那么运算成功,否则发生上溢或下溢,结果是非法的。
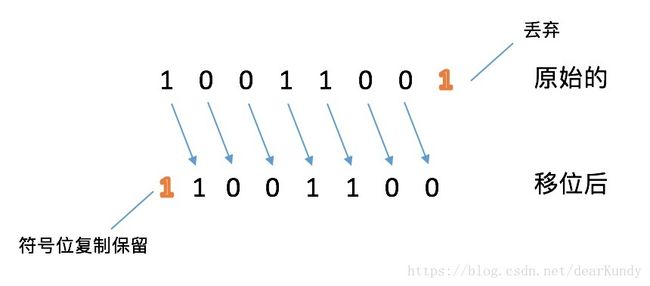
实例1:对位模式10011001使用算术右移,模式是二进制补码格式的整数。
最作左被保留,被复制到相邻的右边的位中。
原始数是-103,新的数是-52。
实例2:对位模式11011001使用算术左移,模式是二进制补码格式的整数。
最左位被丢弃,0作为最右位被插入。
原始数是-39,新的数是-78,原始是被乘以2.因为没有下溢的发生,所以运算合法。
实例3:对位模式01111111使用算术左移,模式是二进制补码格式的整数。
移位后的结果是11111110
原始数是127,新的数是-2。因为上溢发生,所以非法。期望的答案是127×2=254,这个数不能用8位模式表示。
算术运算
本文主要讲的是整数的加减法运算部分。
二进制补码表示法的一个优点是加法和减法之间没有区别。当遇到减法运算时,计算机只简单地把它转变为加法,但要为第二个数求二进制的补。这就意味着我们只需要讨论加法。二进制补码中的加法就像十进制中的加法一样:列与列相加,如果有进位,就加到下一列上。但是,最后一列的进位被舍弃。
运算过程如下:
1)如果运算是减法,则取第二个整数的二进制补码,否则,转下一步。
2)两个整数相加。
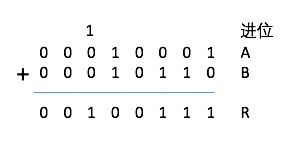
实例1:以二进制补码格式存储的两个正整数相加。
A=(00010001) B=(00010110)
用十进制检查结果:(+17)+(+22)=(+39)。
实例2:以二进制补码格式存储的两个整数相减,最高位进位被舍弃。
A=(11011101) B=(00010100)
用十进制检查结果:(-35)-(+20)=(-55)。
实例3:以二进制补码存储的两个整数相加,结果发生上溢。
A=(01111111) B=(00000011)
我们期望的结果是127+3=130,但答案是-126.错误是由于上溢,因为期望的答案(+130)不再是-128到+127之间的范围。
如有疑问,欢迎随时与博主交流。