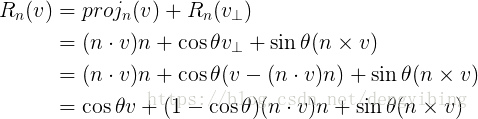四元数做旋转过程的具体证明
文章目录
- 背景
- 万象节锁
- 数学基础
- 旋转以及证明
- 证明过程
- 组合旋转
- 矩阵表示
- 球面线性插值
- 旋转向量
- 参考文档
背景
一般情况下我们都会使用矩阵做旋转变换,绕某个轴或者绕任意向量,这都有在 DirectX数学介绍 做过介绍,虽然直接用矩阵旋转这种方法很直观,但是使用矩阵会遇到两个问题:
- 万象节锁
- 矩阵旋转过程的差值不平滑
万象节锁
旋转过程中,会有一个自由度消失
现有旋转矩阵
E ( h , p , r ) = [ e 00 e 01 e 02 e 10 e 11 e 12 e 20 e 21 e 22 ] = R z ( r ) R x ( p ) R y ( h ) \mathbf{E}(h,p,r)= \begin{bmatrix} e_{00} & e_{01} & e_{02}\\ e_{10} & e_{11} & e_{12}\\ e_{20} & e_{21} & e_{22} \end{bmatrix}= \mathbf{R}_z(r) \mathbf{R}_x(p) \mathbf{R}_y(h) E(h,p,r)=⎣⎡e00e10e20e01e11e21e02e12e22⎦⎤=Rz(r)Rx(p)Ry(h)
先绕z轴旋转角度r,再绕x轴旋转角度p,再绕y轴旋转角度h。
E = [ cos r cos h − sin r sin p sin h − sin r cos p cos r sin h + sin r sin p cos h sin r cos h + cos r sin p sin h cos r cos p sin r sin h − cos r sin p cos h − cos p sin h sin p cos p cos h ] \mathbf{E}= \begin{bmatrix} \cos{r}\cos{h}-\sin{r}\sin{p}\sin{h} & -\sin{r}\cos{p} & \cos{r}\sin{h}+\sin{r}\sin{p}\cos{h}\\ \sin{r}\cos{h}+\cos{r}\sin{p}\sin{h} & \cos{r}\cos{p} & \sin{r}\sin{h}-\cos{r}\sin{p}\cos{h}\\ -\cos{p}\sin{h} & \sin{p} & \cos{p}\cos{h} \end{bmatrix} E=⎣⎡cosrcosh−sinrsinpsinhsinrcosh+cosrsinpsinh−cospsinh−sinrcospcosrcospsinpcosrsinh+sinrsinpcoshsinrsinh−cosrsinpcoshcospcosh⎦⎤
此时,我们假设 cos p = 0 , i . e . , p = ± π / 2 + 2 π k \cos{p}=0,i.e.,p=\pm \pi/2+2\pi k cosp=0,i.e.,p=±π/2+2πk,其中 k k k 是一个整数。这个时候我们就失去了一个自由度,现在矩阵只依赖于一个角, r + h r+h r+h 或者 r − h r-h r−h(不会同时是两个)。
此时旋转矩阵变为
E = [ cos ( r + h ) 0 sin ( r + h ) sin ( r + h ) 0 − cos ( r + h ) 0 1 0 ] \mathbf{E}= \begin{bmatrix} \cos{(r+h)} & 0 & \sin{(r+h)}\\ \sin{(r+h)} & 0 & -\cos{(r+h)}\\ 0 & 1 & 0 \end{bmatrix} E=⎣⎡cos(r+h)sin(r+h)0001sin(r+h)−cos(r+h)0⎦⎤
所以在这种情况下,对 r 和 h 无论怎么旋转,得到的效果都是一样的。
数学基础
- Definition.
q ^ = ( q v , q w ) = i q x + j q y + k q z + q w = q v + q w , q v = i q x + j q y + k q z = ( q x , q y , q z ) , i 2 = j 2 = k 2 = − 1 , j k = − k j = i , k i = − i k = j , i j = − j i = k . \hat \mathbf{q} = ({\mathbf{q}}_v,q_w)=iq_x+jq_y+kq_z+q_w=\mathbf{q}_v+q_w,\\ \mathbf{q}_v = iq_x+jq_y+kq_z = (q_x,q_y,q_z),\\ i^2=j^2=k^2= -1,jk=-kj=i,ki=-ik=j,ij=-ji=k. q^=(qv,qw)=iqx+jqy+kqz+qw=qv+qw,qv=iqx+jqy+kqz=(qx,qy,qz),i2=j2=k2=−1,jk=−kj=i,ki=−ik=j,ij=−ji=k.
其中 q w q_w qw 被称为四元数的实部。 - Multiplication:
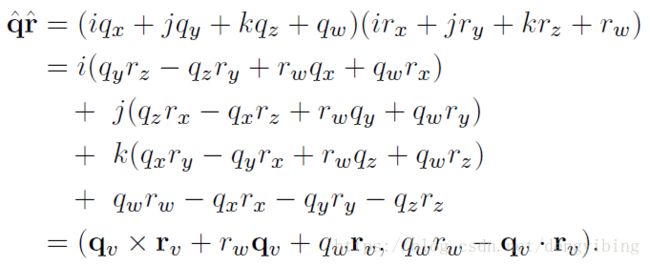
- Addition:
q ^ + r ^ = ( q v , q w ) + ( r v , r w ) = ( q v + r v , q w + r w ) \hat{\mathbf{q}}+\hat{\mathbf{r}}=(\mathbf{q}_v,q_w)+(\mathbf{r}_v,r_w)=(\mathbf{q}_v+\mathbf{r}_v,q_w+r_w) q^+r^=(qv,qw)+(rv,rw)=(qv+rv,qw+rw) - Conjugate:
q ^ ∗ = ( q v , q w ) ∗ = ( − q v , q w ) \hat{\mathbf{q}}^*=(\mathbf{q}_v,q_w)^*=(-\mathbf{q}_v,q_w) q^∗=(qv,qw)∗=(−qv,qw) - Norm:
n ( q ) = q ^ ∗ q ^ = q v ⋅ q v + q w 2 = q x 2 + q y 2 + q z 2 + q w 2 n(\mathbf{q})=\sqrt{\hat{\mathbf{q}}^*\hat{\mathbf{q}}}=\sqrt{\mathbf{q}_v \cdot \mathbf{q}_v + q_w^2} = \sqrt{q_x^2+q_y^2+q_z^2+q_w^2} n(q)=q^∗q^=qv⋅qv+qw2=qx2+qy2+qz2+qw2 - Identity:
i ^ = ( 0 , 1 ) \hat{\mathbf{i}}=(\mathbf{0},1) i^=(0,1)
其中要有 q ^ − 1 q ^ = q ^ q ^ − 1 = 1 \hat{\mathbf{q}}^{-1}\hat{\mathbf{q}}=\hat{\mathbf{q}}\hat{\mathbf{q}}^{-1}=1 q^−1q^=q^q^−1=1 - Inverse:
q ^ − 1 = 1 n ( q ^ ) 2 q ^ ∗ \hat{\mathbf{q}}^{-1} =\frac{1}{n(\hat{\mathbf{q}})^2}\hat{\mathbf{q}}^* q^−1=n(q^)21q^∗ - Conjugate rules:
( q ^ ∗ ) ∗ = q ^ , ( q ^ + r ^ ) ∗ = q ^ ∗ + r ^ ∗ , ( q ^ r ^ ) ∗ = r ^ ∗ q ^ ∗ (\hat{\mathbf{q}}^*)^*=\hat{\mathbf{q}},\\ (\hat{\mathbf{q}}+\hat{\mathbf{r}})^*=\hat{\mathbf{q}}^*+\hat{\mathbf{r}}^*,\\ (\hat{\mathbf{q}}\hat{\mathbf{r}})^*=\hat{\mathbf{r}}^*\hat{\mathbf{q}}^* (q^∗)∗=q^,(q^+r^)∗=q^∗+r^∗,(q^r^)∗=r^∗q^∗ - Norm rules:
n ( q ^ ∗ ) = n ( q ^ ) , n ( q ^ r ^ ) = n ( q ^ ) n ( r ^ ) n(\hat{\mathbf{q}}^*)=n(\hat{\mathbf{q}}),\\ n(\hat{\mathbf{q}}\hat{\mathbf{r}})=n(\hat{\mathbf{q}})n(\hat{\mathbf{r}}) n(q^∗)=n(q^),n(q^r^)=n(q^)n(r^) - Linearity:
p ^ ( s q ^ + t r ^ ) = s p ^ q ^ + t p ^ r ^ , ( s p ^ + t q ^ ) r ^ = s p ^ r ^ + t q ^ r ^ \hat{\mathbf{p}}(s\hat{\mathbf{q}}+t\hat{\mathbf{r}})=s\hat{\mathbf{p}}\hat{\mathbf{q}}+t\hat{\mathbf{p}}\hat{\mathbf{r}},\\ (s\hat{\mathbf{p}}+t\hat{\mathbf{q}})\hat{r}=s\hat{\mathbf{p}}\hat{\mathbf{r}}+t\hat{\mathbf{q}}\hat{\mathbf{r}} p^(sq^+tr^)=sp^q^+tp^r^,(sp^+tq^)r^=sp^r^+tq^r^ - Associativity:
p ^ ( q ^ r ^ ) = ( p ^ q ^ ) r ^ \hat{\mathbf{p}}(\hat{\mathbf{q}}\hat{\mathbf{r}})=(\hat{\mathbf{p}}\hat{\mathbf{q}})\hat{\mathbf{r}} p^(q^r^)=(p^q^)r^
根据之前的性质, q ^ \hat{\mathbf{q}} q^ 可以被写成
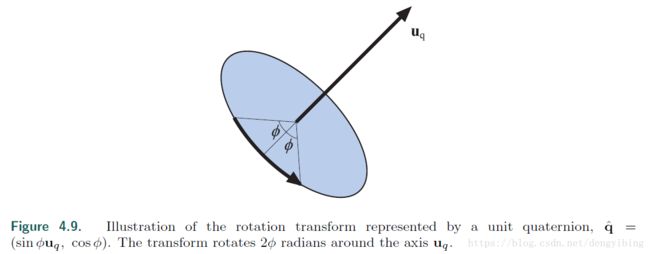
q ^ = ( sin ϕ u q , cos ϕ ) = sin ϕ u q + cos ϕ \hat{\mathbf{q}}=(\sin{\phi \mathbf{u_q}}, \cos{\phi})=\sin{\phi \mathbf{u_q}}+\cos{\phi} q^=(sinϕuq,cosϕ)=sinϕuq+cosϕ
还是有 ∣ ∣ u q ∣ ∣ = 1 ||u_q||=1 ∣∣uq∣∣=1.
而对于复数,二维的单位向量可以被写为 cos ϕ + i sin ϕ = e i ϕ \cos \phi + i\sin \phi = e^{i\phi} cosϕ+isinϕ=eiϕ。则四元数相同的写法如下:
q ^ = sin ϕ u q + cos ϕ = e ϕ u q \hat{\mathbf{q}}=\sin{\phi}\mathbf{u_q}+\cos{\phi}=e^{\phi\mathbf{u_q}} q^=sinϕuq+cosϕ=eϕuq - Logarithm:
log ( q ^ ) = log ( e ϕ u q ) = ϕ u q \log(\hat{\mathbf{q}})=\log(e^{\phi \mathbf{u_q}})=\phi \mathbf{u_q} log(q^)=log(eϕuq)=ϕuq - Power:
q ^ t = ( s i n ϕ u q + cos ϕ ) t = e ϕ t u q = sin ( ϕ t ) u q + cos ( ϕ t ) \hat{\mathbf{q}}^t=(sin{\phi}\mathbf{u_q}+\cos{\phi})^t=e^{\phi t\mathbf{u_q}}=\sin{(\phi t)}\mathbf{u_q}+\cos{(\phi t)} q^t=(sinϕuq+cosϕ)t=eϕtuq=sin(ϕt)uq+cos(ϕt)
旋转以及证明
四元数最重要的一个性质是单位四元数可以表示任意三维旋转
首先把一个顶点或向量的四位数 p = ( p x , p y , p z , p w ) T \mathbf{p}=(p_x,p_y,p_z,p_w)^T p=(px,py,pz,pw)T 放到四元数中 p ^ \mathbf{\hat{p}} p^,假设我们有一个单位四元数 q ^ = ( s i n ϕ u q + cos ϕ ) \mathbf{\hat{q}}=(sin{\phi}\mathbf{u_q}+\cos{\phi}) q^=(sinϕuq+cosϕ)。则下面的式子表 示 p ^ \mathbf{\hat{p}} p^ 绕轴 u q \mathbf{u_q} uq 旋转 2 ϕ 2\phi 2ϕ 的角度。
q ^ p ^ q ^ − 1 \hat{q}\hat{p}\hat{q}^{-1} q^p^q^−1
因为 q ^ \mathbf{\hat{q}} q^ 是单位四元数, q ^ − 1 = q ^ ∗ \hat{q}^{-1}=\hat{q}^* q^−1=q^∗。所以 q ^ \hat{q} q^ 与 − q ^ -\hat{q} −q^ 表示相同的旋转。
证明过程
u ⃗ \vec{u} u 是一个单位向量(旋转轴), q = cos α 2 + u ⃗ sin α 2 q=\cos{\frac{\alpha}{2}}+\vec{u}\sin{\frac{\alpha}{2}} q=cos2α+usin2α。我们的目标是证明
v ′ ⃗ = q v ⃗ q − 1 = ( cos α 2 + u ⃗ sin α 2 ) v ⃗ ( cos α 2 − u ⃗ sin α 2 ) \vec{v^{\prime}}=q\vec{v}q^{-1}= (\cos{\frac{\alpha}{2}}+\vec{u}\sin{\frac{\alpha}{2}}) \vec{v} (\cos{\frac{\alpha}{2}}-\vec{u}\sin{\frac{\alpha}{2}}) v′=qvq−1=(cos2α+usin2α)v(cos2α−usin2α)
表示向量 v ⃗ \vec{v} v 绕着轴 u ⃗ \vec{u} u 旋转 α \alpha α 角度

其中 v ⃗ ⊥ \vec{v}_{\perp} v⊥ 和 v ⃗ ∥ \vec{v}_{\parallel } v∥ 分别是 v ⃗ \vec{v} v 各自垂直和平行于 u ⃗ \vec{u} u 的部分。
所以就证明了旋转的正确性。
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ \vec{v^{\prime…
组合旋转
对于两个用于表示旋转的四元数 r ⃗ \vec{r} r 和 q ⃗ \vec{q} q。对 p 首先用 q ⃗ \vec{q} q 旋转,然后用 r ⃗ \vec{r} r 旋转,可以表示为如下:
r ⃗ ( q ⃗ p ⃗ q ⃗ ∗ ) r ⃗ ∗ = ( r ⃗ q ⃗ ) p ⃗ ( r ⃗ q ⃗ ) ∗ = c ⃗ p ⃗ c ⃗ ∗ \vec{r}(\vec{q}\vec{p}\vec{q}^*)\vec{r}^*=(\vec{r}\vec{q})\vec{p}(\vec{r}\vec{q})^*=\vec{c}\vec{p}\vec{c}^* r(qpq∗)r∗=(rq)p(rq)∗=cpc∗
其中 c ⃗ = r ⃗ q ⃗ \vec{c}=\vec{r}\vec{q} c=rq 表示两个旋转的连接。
矩阵表示
一个四元数 q ⃗ \vec{q} q 可以转换为一个矩阵 M q M^q Mq
M q = [ 1 − s ( q y 2 + q z 2 ) s ( q x q y − q w q z ) s ( q x q z + q w q y ) 0 s ( q x q y + q w q z ) 1 − s ( q x 2 + q z 2 ) s ( q y q z − q w q x ) 0 s ( q x q z − q w q y ) s ( q y q z + q w q x ) 1 − s ( q x 2 + q y 2 ) 0 0 0 0 1 ] M^q= \begin{bmatrix} 1-s(q_y^2+q_z^2) & s(q_xq_y-q_wq_z) & s(q_xq_z+q_wq_y) & 0\\ s(q_xq_y+q_wq_z) & 1-s(q_x^2+q_z^2) & s(q_yq_z-q_wq_x) & 0\\ s(q_xq_z-q_wq_y) & s(q_yq_z+q_wq_x) & 1-s(q_x^2+q_y^2) & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} Mq=⎣⎢⎢⎡1−s(qy2+qz2)s(qxqy+qwqz)s(qxqz−qwqy)0s(qxqy−qwqz)1−s(qx2+qz2)s(qyqz+qwqx)0s(qxqz+qwqy)s(qyqz−qwqx)1−s(qx2+qy2)00001⎦⎥⎥⎤
这里 s = 2 / ( n ( q ^ ) ) 2 s=2/(n(\hat{\mathbf{q}}))^2 s=2/(n(q^))2。对于单位四元数
M q = [ 1 − 2 ( q y 2 + q z 2 ) 2 ( q x q y − q w q z ) 2 ( q x q z + q w q y ) 0 2 ( q x q y + q w q z ) 1 − 2 ( q x 2 + q z 2 ) 2 ( q y q z − q w q x ) 0 2 ( q x q z − q w q y ) 2 ( q y q z + q w q x ) 1 − 2 ( q x 2 + q y 2 ) 0 0 0 0 1 ] M^q= \begin{bmatrix} 1-2(q_y^2+q_z^2) & 2(q_xq_y-q_wq_z) & 2(q_xq_z+q_wq_y) & 0\\ 2(q_xq_y+q_wq_z) & 1-2(q_x^2+q_z^2) & 2(q_yq_z-q_wq_x) & 0\\ 2(q_xq_z-q_wq_y) & 2(q_yq_z+q_wq_x) & 1-2(q_x^2+q_y^2) & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} Mq=⎣⎢⎢⎡1−2(qy2+qz2)2(qxqy+qwqz)2(qxqz−qwqy)02(qxqy−qwqz)1−2(qx2+qz2)2(qyqz+qwqx)02(qxqz+qwqy)2(qyqz−qwqx)1−2(qx2+qy2)00001⎦⎥⎥⎤
从矩阵表示到四元数
m 21 q − m 12 q = 4 q w q x , m 02 q − m 20 q = 4 q w q y , m 10 q − m 01 q = 4 q w q z m_{21}^q-m_{12}^q=4q_wq_x,\\ m_{02}^q-m_{20}^q=4q_wq_y,\\ m_{10}^q-m_{01}^q=4q_wq_z m21q−m12q=4qwqx,m02q−m20q=4qwqy,m10q−m01q=4qwqz
矩阵的秩
t r ( M q ) = 4 − 2 s ( q x 2 + q y 2 + q z 2 ) = 4 ( 1 − q x 2 + q y 2 + q z 2 q x 2 + q y 2 + q z 2 + q w 2 ) = 4 q w 2 q x 2 + q y 2 + q z 2 + q w 2 = 4 q w 2 ( n ( q ^ ) ) 2 tr(M^q)=4-2s(q_x^2+q_y^2+q_z^2)=4(1-\frac{q_x^2+q_y^2+q_z^2}{q_x^2+q_y^2+q_z^2+q_w^2})=\frac{4q_w^2}{q_x^2+q_y^2+q_z^2+q_w^2}=\frac{4q_w^2}{(n(\hat{q}))^2} tr(Mq)=4−2s(qx2+qy2+qz2)=4(1−qx2+qy2+qz2+qw2qx2+qy2+qz2)=qx2+qy2+qz2+qw24qw2=(n(q^))24qw2
四元数每个分量的值
q w = 1 2 t r ( M q ) , q x = m 21 q − m 12 q 4 q w , q y = m 02 q − m 20 q 4 q w , q z = m 10 q − m 01 q 4 q w q_w=\frac{1}{2}\sqrt{tr(M^q)},\\ q_x=\frac{m_{21}^q-m_{12}^q}{4q_w},\\ q_y=\frac{m_{02}^q-m_{20}^q}{4q_w},\\ q_z=\frac{m_{10}^q-m_{01}^q}{4q_w} qw=21tr(Mq),qx=4qwm21q−m12q,qy=4qwm02q−m20q,qz=4qwm10q−m01q
球面线性插值
s ^ ( q ^ , r ^ , t ) = ( r ^ q ^ − 1 ) t q ^ \hat{\mathbf{s}}(\hat{\mathbf{q}},\hat{\mathbf{r}},t)=(\hat{\mathbf{r}}\hat{\mathbf{q}}^{-1})^t\hat{\mathbf{q}} s^(q^,r^,t)=(r^q^−1)tq^
对于用软件实现,更直观的是
s ^ ( q ^ , r ^ , t ) = s l e r p ( q ^ , r ^ , t ) = sin ( ϕ ( 1 − t ) ) sin ϕ q ^ + sin ( ϕ t ) sin ϕ r ^ \hat{\mathbf{s}}(\hat{\mathbf{q}},\hat{\mathbf{r}},t)= slerp(\hat{\mathbf{q}}, \hat{\mathbf{r}}, t)= \frac{\sin(\phi(1-t))}{\sin \phi}\hat{\mathbf{q}}+\frac{\sin(\phi t)}{\sin \phi}\hat{\mathbf{r}} s^(q^,r^,t)=slerp(q^,r^,t)=sinϕsin(ϕ(1−t))q^+sinϕsin(ϕt)r^
其中
cos ϕ = q x r x + q y r y + q z r z + q w r w \cos \phi = q_xr_x+q_yr_y+q_zr_z+q_wr_w cosϕ=qxrx+qyry+qzrz+qwrw
但是这样的计算其实很费时,有快速计算的方法。iSlerp
旋转向量
通过最短路径,从向量 s 旋转到 t。
旋转轴为 u = ( s × t ) / ∣ ∣ s × t ∣ ∣ u=(s \times t)/||s \times t|| u=(s×t)/∣∣s×t∣∣。有 e = s ⋅ t = cos ( 2 ϕ ) e=s \cdot t=\cos(2\phi) e=s⋅t=cos(2ϕ) 和 ∣ ∣ s × t ∣ ∣ = sin ( 2 ϕ ) ||s \times t||=\sin(2\phi) ∣∣s×t∣∣=sin(2ϕ)。则 q ^ = ( sin ϕ sin 2 ϕ ( s × t ) , cos ϕ ) \hat{q}=(\frac{\sin\phi}{\sin 2\phi}(s \times t), \cos \phi) q^=(sin2ϕsinϕ(s×t),cosϕ)
最终有
q ^ = ( q v , q w ) = ( 1 2 ( 1 + e ) ( s × t ) , 2 ( 1 + e ) 2 ) \hat{q}=(q_v,q_w)=(\frac{1}{\sqrt{2(1+e)}}(s \times t), \frac{\sqrt{2(1+e)}}{2}) q^=(qv,qw)=(2(1+e)1(s×t),22(1+e))
表示成矩阵形式为旋转矩阵
R ( s , t ) = [ e + h v x 2 h v x v y − v z h v x v z + v y 0 h v x v y + v z e + h v y 2 h v y v z − v x 0 h v x v z − v y h v y v z + v x e + h v z 2 0 0 0 0 1 ] R(s,t)= \begin{bmatrix} e+hv_x^2 & hv_xv_y-v_z & hv_xv_z+v_y & 0\\ hv_xv_y+v_z & e+hv_y^2 & hv_yv_z-v_x & 0\\ hv_xv_z-v_y & hv_yv_z+v_x & e+hv_z^2 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} R(s,t)=⎣⎢⎢⎡e+hvx2hvxvy+vzhvxvz−vy0hvxvy−vze+hvy2hvyvz+vx0hvxvz+vyhvyvz−vxe+hvz200001⎦⎥⎥⎤
其中
v = s × t , e = cos ( 2 ϕ ) = s ⋅ t , h = 1 − cos ( 2 ϕ ) sin 2 ( 2 ϕ ) = 1 − e v ⋅ v = 1 1 + e . v=s \times t,\\ e = \cos(2\phi)=s \cdot t,\\ h=\frac{1-\cos(2\phi)}{\sin^2(2\phi)}=\frac{1-e}{v \cdot v}=\frac{1}{1+e}. v=s×t,e=cos(2ϕ)=s⋅t,h=sin2(2ϕ)1−cos(2ϕ)=v⋅v1−e=1+e1.
参考文档
Real-Time Rendering, Fourth Edition