计算机图形学-五角星的画法

话不多说直接上实现效果图：

以下是步骤，首先看看如何确定点的坐标。

有以下说明：

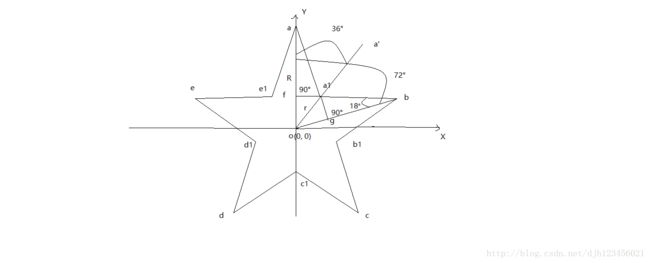
① 坐标原点o（0,0）为坐标原点

② 五角星的长轴为R = |oa|,长度已知

③ 五角星的短轴为r = |oa1|

④ 弧度制为rad = π/180 rad

 

五角星分为以下几个步骤：

① 求五角星外五个顶点的坐标（a,b, c, d, e）

由图可知：∠fbg = 18°,∠aoa’ = ∠a’ob = 36°, ∠aob = 72°

由极坐标公式：

可以得到外五角星的五个坐标：

（(R * cos(90°+ k * 72°+ yDegree)), (R * sin(90°+ k * 72°+ yDegree))）其中k = 0、1、2、3、4， yDegree为oa与y轴的夹角（如下图），默认为0。

但画图时会由中心点O（x， y）确定五角星外五个顶点的坐标，经过坐标变换为：

（x -(R * cos(90°+ k * 72°+ yDegree)),  y - (R * sin(90°+ k * 72°+yDegree))）

 

 

②求解五角星内五顶点坐标(a1, b1, c1,d1, e1)

由图可知：r * cos(36°)  = |fo| = R * sin(18°)

所以：r = R * sin(18°) / cos(36°);

根据步骤①相同方法得到五角星内五顶点坐标：

（(R* cos(90°+ 36°+ k * 72°+yDegree)), (R * sin(90°+ 36°+ k * 72°+yDegree))）其中k = 0、1、2、3、4， yDegree为oa与y轴的夹角，默认为0。

 

但画图时会由中心点O（x， y）确定五角星外五个顶点的坐标，经过坐标变换为：

（x -(R * cos(90°+ 36°+ k * 72°+yDegree)),  y - (R * sin(90°+ 36°+ k* 72°+ yDegree))）

 

③开始画图

  得到顶点坐标后，选择绘制封闭图形，用画刷填充颜色根据k值（0、1、2、3、4）来选择。如下图，此时为k=0时，用不同颜色的画刷分别填①，③区域。

① 程序实现

/*
int R:五角星的长轴
int x, y:五角星的中心点
int yDegree:长轴与y轴的夹角
*/
void pentagram(CDC* pDC, intR, int x, int y, int yDegree = 0)
{
    double rad = 3.1415926 / 180;                    //每度的弧度值
    double r = R * sin(18 * rad) / cos(36 * rad);    //五角星短轴的长度
    POINT RVertex[5], rVertex[5];
    for (int k = 0; k < 5; k++)                      //求取坐标
    {
       RVertex[k] = { int(x - (R * cos((90 + k * 72 + yDegree) *rad))), int(y - (R * sin((90 + k * 72 + yDegree) * rad)) ) };
       rVertex[k] = { int(x - (r * cos((90 + 36 + k * 72 + yDegree) *rad))), int(y - (r * sin((90 + 36 + k * 72 + yDegree) * rad))) };
    }
 
    CBrush pNewBrush(RGB(255, 255, 0));
    CBrush pNewBrush1(RGB(238, 154, 0));
 
    for (int i = 0; i < 5; i++)
    {
       POINT polylinepoint[4] = {RVertex[i], rVertex[i], { x, y },RVertex[i] };
       POINT polylinepoint1[4] = {RVertex[(i+1) % 5], rVertex[i], {x, y }, RVertex[(i + 1) % 5] };
        
       pDC->SelectObject(pNewBrush1);
       pDC->Polygon(polylinepoint, 4);
       pDC->SelectObject(pNewBrush);
       pDC->Polygon(polylinepoint1, 4);
      
    }
}