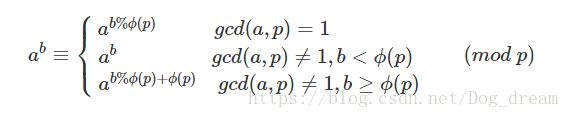ACM-ICPC 2018 焦作赛区网络预赛 -I Give Candies(扩展欧拉定理+大数取模)
There are NN children in kindergarten. Miss Li bought them NN candies. To make the process more interesting, Miss Li comes up with the rule: All the children line up according to their student number (1...N)(1...N), and each time a child is invited, Miss Li randomly gives him some candies (at least one). The process goes on until there is no candy. Miss Li wants to know how many possible different distribution results are there.
Input
The first line contains an integer TT, the number of test case.
The next TT lines, each contains an integer N.
1 \le T \le 1001≤T≤100
1 \le N \le 10^{100000}1≤N≤10100000
Output
For each test case output the number of possible results (mod 1000000007).
样例输入复制
1
4样例输出复制
8题目来源
ACM-ICPC 2018 焦作赛区网络预赛
题解：
由题目可推出：
;毫无疑问只是一道大数取模的题
由欧拉公式可知 gcd(2,1000000007)=1;所以：
% 1000000007=2^(n % φ(1000000007));
φ(1000000007)=1000000006;
由余数定理可知:(a+b)%d=(a%d+b%d)%d a*b%d=(a%d*b%d)%d;
所以n可以用字符串存取然后每次乘10相加 取模就好。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include