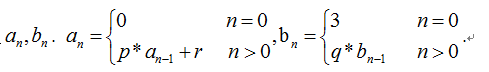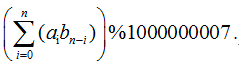51nod 1341 混合序列

当给定p,q,r时，我们可以定义

对于给定的p,q,r,n，请计算

对于p=2 q=2 r=1 n=1这组数据，

所以答案是

Input

共1行，4个整数数p, q, r, n中间用空格分隔(1 <= p, q, r, n<=1000000000)。

OutPut

对于每一个数据，在一行中输出答案。

Input示例

2 2 1 1

Output示例

3

 

这是个数论问题，首先根据p，q是否等于1这一条件分了四种情况。求出每种情况下的结果表达式，发现是一个分数求模的问题，利用乘法逆元把分母用其逆元代替,再用快速幂将大分子逐一求模化简，得到答案。。。

#include                         //分数求模 乘法逆元 
typedef long long LL;
const LL mod = 1000000007;
LL po(LL k)  
{  
    LL ret=1;  
    LL m=mod-2;  
    while(m)  
    {  
        if(m&1)ret=ret*k%mod;  
        k=k*k%mod;  
        m>>=1;  
    }  
    return ret;  
}    
LL power(LL a,LL b)  
{  
    LL ans = 1;  
    a %= mod;  
    while(b)  
    {  
        if(b & 1)  
        {  
            ans = ans * a % mod;  
            b--;  
        }  
        b >>= 1;  
        a = a * a % mod;  
    }  
    return ans;  
} 
LL work(LL a,LL n){
	return ((power(a,n)-1+mod)%mod*po(a-1))%mod;
}
int main()
{
    LL p,q,r,n;
	int ans;
	//while(1){
    scanf("%lld%lld%lld%lld",&p,&q,&r,&n);
    if(p==1&&q==1){
    	ans=( ( n*(n+1)/2)%mod * ( (3*r)%mod ) )%mod;
    	printf("%d\n",ans);
    } 
    else if(p==1&&q!=1){
    	LL t=((q-1)*(q-1))%mod; 
    	ans=(( (  power(q,n) - 1 + mod ) % mod * ( ( (3*r*q) % mod * po(t) ) %mod ) )%mod-((3*r*n)%mod*(po(q-1))%mod)+mod)%mod;
    	printf("%d\n",ans);
    }
    else if(q==1&&p!=1){
    	LL t=((p-1)*(p-1))%mod;
    	ans=(( (power(p,n+1)-1+mod)%mod * (  (  (3*r)%mod * po(t))%mod  ) )%mod - (  ((n+1)*3*r)%mod * po(p-1))%mod + mod )%mod;
    	printf("%d\n",ans);
    }
    else if(q==p){
    	ans=((power(q,n)*(( (3*r*(n+1))%mod*po(p-1))%mod))%mod-(work(q,n+1) * (( (3*r)%mod * po(p-1) )%mod) )%mod+mod)%mod;
    	printf("%d\n",ans);
    }
    else {
    	if(q>p){
    		ans=( ( ( (power(q,n+1)-power(p,n+1)+mod)%mod * po(q-p))%mod *(( (3*r)%mod * po(p-1) )%mod))%mod-( work(q,n+1) * (((3*r)%mod*po(p-1))%mod))%mod+mod)%mod;
		}
        else {
        	ans=( ( ( (power(p,n+1)-power(q,n+1)+mod)%mod * po(p-q))%mod *(( (3*r)%mod * po(p-1) )%mod))%mod-( work(q,n+1) * (((3*r)%mod*po(p-1))%mod))%mod+mod)%mod;
        }
		printf("%d\n",ans);
    }
//}
    return 0;
}