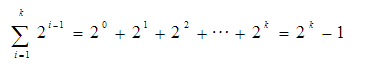树和二叉树
1、树的定义
树(Tree)是由 一个 或 多个结点 组成的有限集合T,且满足:
①有且仅有一个称为根的结点;
②其余结点分成n(n≥0)个互不相交的集合T1,T2,…Tn,其中每个集合都是一棵树,并且称Ti (1≤i≤n) 为根的子树。
显然树是一个递归定义。
图1.3是一棵具有13个结点的树,其中A结点是树的根,其余12个结点划分为3个互不相交的子集:
T1 = { B, E ,F, K, L } T2 = {C ,G }
T3 = { D, H, I, J, M }
T1, T2, T3 均是根A的子树,其本身也都是树。我们还可以继续划分,集合{E, K L}是B的子树,以此类推。所以我们除了用图来表示树的结构,还可用广义表来表示树,例如,图1.3的树用广义表表示如下:
T=(A(B(E(K,L),F)),C(G),D(H(M),I,J)))
2、树的基本术语
因为树的结构比其他线性结构更复杂,所以我们需要用一些术语来描述结点和结点之间的关系。
①根结点
每一棵树都有一个根结点,如图1.3中A结点。根据树的定义,树中的每一个结点都可以看成是它的一个子树的根。
如结点B, C, D分别是子树T1, T2, T3的根结点。但是A结点与其它结点不同的是,只有后继结点而没有前趋结点,所以
A被称为树的根。
②结点的度和树的度
一个结点的子树的个数称为是该结点的度。如根结点A有3个子树,则A结点的度为3;而C结点只有1
个子树,则C结点的度为1。树中度数最大的结点的度为树的度。树T的度是3。
③分支结点和叶结点
度为0的结点称为叶结点或端结点。如K, L, F, G, M, I, J,这些结点都是树的叶结点。度大于0的结点称作分支结点。
④子结点和父结点
每个结点的子树的根结点称为该结点的儿子(子结点),而该结点称为子结点的父亲(父结点)。如A结点为B结点的父结点,B
为A的子结点。树中的一条边连接两个结点,这两个结点互为父子关系。有同一个父结点的所有子结点称为兄弟。如B, C, D就互为兄弟。
某结点到整棵树的根结点的路径上的所有结点叫作该结点的祖先。如结点K到根结点A的路径上的所有结点E, B, A,都是结点K的祖先。
⑤结点的层数和树的深度
树既是一种递归结构,也是一种层次结构,树中的每个结点都处在一定的层数上。结点的层数从树根开始定义,设根结点的层号为1,其儿子结点的层号为2,以此类推;若某结点在第L层,则该结点的儿子处于第L+1层。树中结点最大的层号为树的深度。树T的深度为4。
⑥ 有序树和无序树
若结点的子树有次序排列,且先后次序不能互换,这样的树称为有序树,反之为无序树。
⑦ 森林
森林是若干棵互不相交的树的集合。若删除图1.3中树T的根结点A,就得到一个森林{T1, T2, T3}。
1、二叉树的定义
如果树中每个结点的子树个数小于或等于2的树,并且各子树的次序不能互换,有左、右子树之分,这样的树称为二叉树。所以二叉树是一种度为2的有序树。
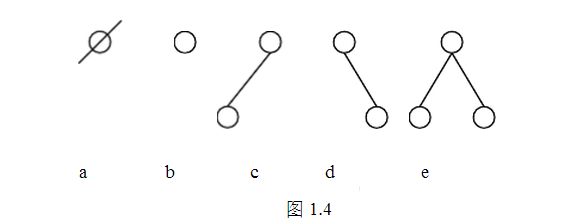
根据定义,二叉树共有5种不同的基本形态,如图1.4所示。
a. 空二叉树;
b. 只有一个根结点的二叉树;
c. 右子树为空的二叉树;
d. 左子树为空的二叉树;
e. 左、右子树非空的二叉树。
2、二叉树的性质
性质1 在二叉树中,第i层的结点总数不超过2i-1(i>=1);
性质2 深度为k的二叉树的结点总数不超过2k-1(k>=1)。
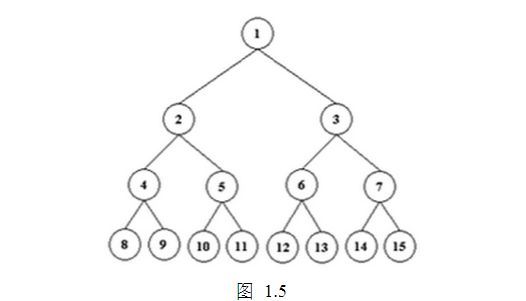
请看图1.5中的二叉树:
第1层 1个结点,20
第2层 2个结点,21 第3层 4个结点,22
第I层 2i-1个结点;
那么对于深度为k的二叉树所具有的结点总数为:
如果一个深度为K的二叉树,具有2k-1个结点,则称该二叉树为满二叉树。如图1.5是深度为4的满二叉树,它的结点总数是15。满二叉树最底一层的各个结点的度数为0,而其余的结点的度数均为2。
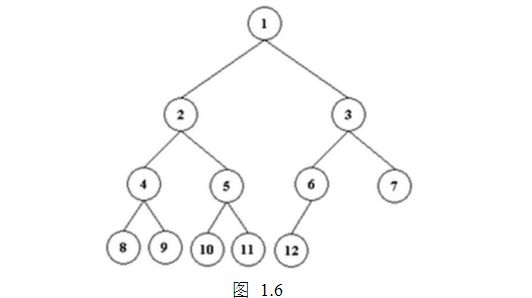
如果一棵深度为K二叉树,1至k-1层的结点都是满的,即满足2i-1,只有最下面的一层的结点数小于2i-1,并且最下面一层的结点都集中在该层最左边的若干位置,则此二叉树称为完全二叉树。如图1.6所示。
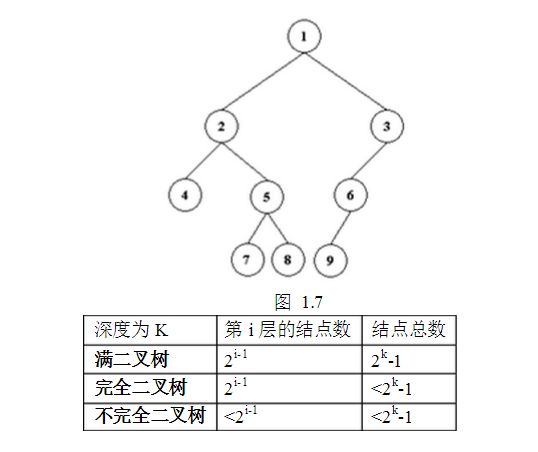
如果二叉树的中间有些结点不存在,如图1.7所示二叉树,称为不完全二叉树
性质3 在任意一棵二叉树中,度为0的结点(叶结点)比度为2的结点多一个。
在二叉树中,如果其叶结点的个数为N0,其度数为2的结点总数为N2,则有: N0=N2+1。
例如:图1.5的树,n0=8, n2=7
图 1.7的树,n0=4, n2=3
性质4 具有n个结点的二叉树,其深度至少为[log2n]+1,其中[log2n]表示取log2n的整数部分。
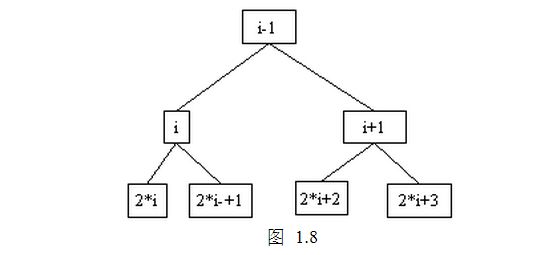
对于完全二叉树,还有如下性质: 1) 在完全二叉树中,深度K与结点总数N的关系为:K=[Log2N]+1,且有如下关系:2k-11,则父结点为[i/2]。
如果2*I>N,则I无左子树;如果2*I<=N,则I的左儿子的编号为2*I。
如果2*I+1>N,则I无右子树;如果2*I+1<=N,则I的右儿子的编号为2*I+1。
3、 二叉树的存储结构
二叉树的存储结构有两种形式:
1) 顺序存储方式;
2) 链表存储方式。
【顺序存储方式】
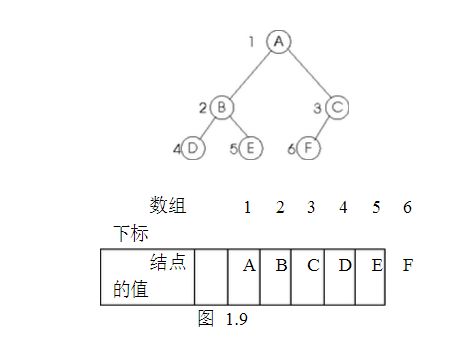
对于满二叉树和完全二叉树,可以对每个结点进行连续编号,所以通常采用顺序存储的方式。具体做法是:定义一个一维数组,把每个结点的编号作为数组的下标变量,将结点的值存放在数组中。二叉树的各结点的编号从根结点开始,根结点的标号为1,然后,逐层由左向右进行连续编号,并将该结点的值存于对应编号为下标的一维数组中。如图1.9所示。
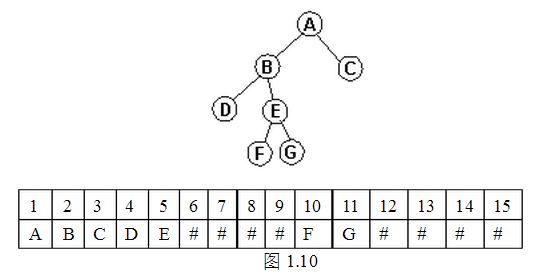
如图1.10所示的不完全二叉树,也可以用顺序存储的形式。将不完全二叉树缺掉的结点补齐,然后以满二叉树编号方式进行编号,以编号顺序将该树的各结点存放在一维数组中。由此看出,6,7,8,9,12,13,14,15的单元里是没有存放数据的,而这样的不完全二叉树实际上只有7个结点,却要占用15个存储单元,不免浪费空间。
但是,在这种存储方式下,从一个结点的编号就可以推测其父结点,左右子结点的编号,据此,可以轻易画出二叉树。
【链表存储方式】
用链接表存储二叉树,每个结点由三部分组成:数据域、左地址域、右地址域。左指针、右指针分别指向该结点的左儿子和右儿子的地址域。见图1.12。
每个结点的数据格式为:
4. 二叉树的遍历
二叉树的遍历是根据一定的规律访问二叉树的每一个结点,所谓访问,可以是打印该结点的值,修改该结点的值,或将该结点做某些处理等。
二叉树的遍历是二叉树必须掌握的知识点,一般面试都会碰到根据已知遍历序列求出要求序列,只要真正掌握了遍历的方法,这类问题也就很简单了。
根据根结点,左子树,右子树先后访问的不同顺序,可以有以下六种不同的遍历方式:
①根,左,右;
②左,根,右;
③左,右,根;
④根,右,左;
⑤右,左,根;
⑥右,根,左。
二叉树最常用的遍历运算是:
①先序遍历,根,左,右;
②中序遍历,左,根,右;
③后序遍历,左,右,根。
1) 先序遍历:
先访问根结点,再先序遍历左子树,最后再先序遍历右子树。
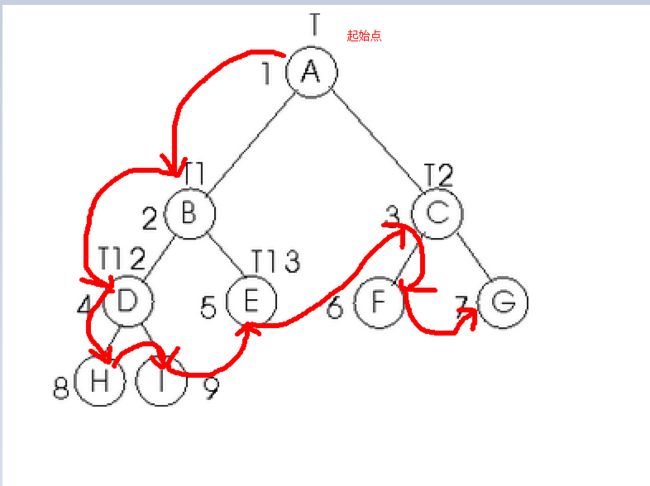
图1.13按先序遍历 各结点被访问的顺序为:ABDHIECFG
2)中序遍历:
先中序遍历左子树,然后再访问根结点,最后再中序遍历右子树。
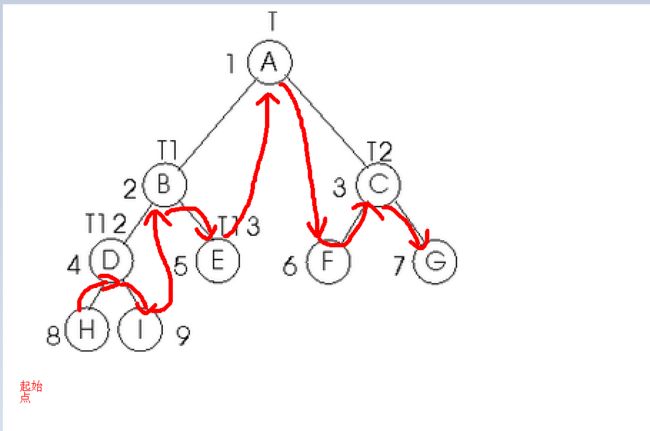
图1.13按中序遍历 各结点被访问的顺序为:HDIBEAFCG
3) 后序遍历:
先后序遍历左子树,然后再后序遍历右子树,最后再访问根结点。
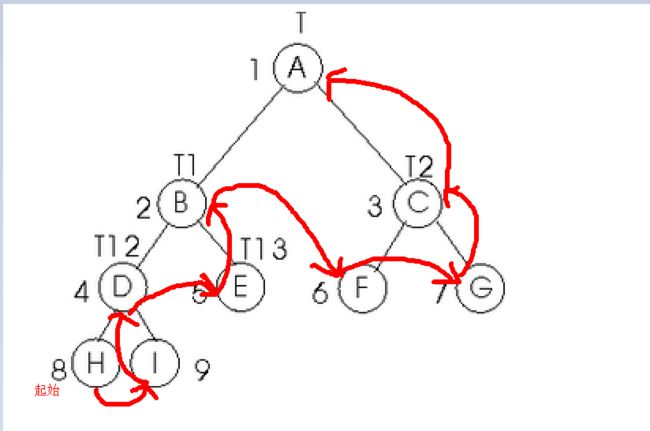
对图1.13的二叉树进行后序遍历,访问各个结点的顺序为:HIDEBFGCA
遍历算法案例:
给出一棵二叉树的中序遍历:DBGEACHFI与后序遍历:DGEBHIFCA,画出此二叉树(求先序遍历的话连二叉树都出来了还不简单?)。
问题分析:
后序遍历中最后访问的是根结点,所以后序遍历DGEBHIFCA序列中A是根结点;
根据中序遍历的算法,先中序遍历左子树,然后再访问根结点,最后再中序遍历右子树,所以中序遍历DBGEACHFI序列中,根结点A的两侧分别是左子树和右子树:DBGE、CHFI。
对左子树的中序遍历DBGE、后序遍历DGEB
用上面的方法分析,得知B是左子树的根结点,D是B的左子树,GE是B的右子树。
同理可以推出E是G的父结点,G是E的左儿子。
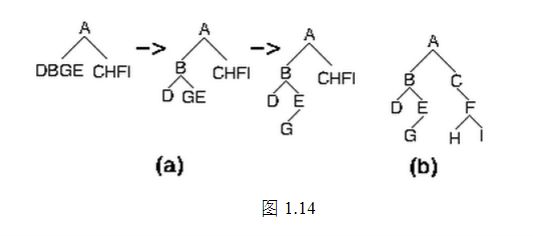
上述推导过程如图1.14 a所示,最后的结果如图1.14 b所示。
以上就是二叉树的三种遍历算法,其实还有一个层次遍历,有兴趣的可以自己去了解一下
本来想着弄二叉搜索树的,但是想先把定义之类的理一下,找了很多资料综合自己以前学的,整理了一下书和二叉树的基本概念。
在这里还有一个坑:就是二叉树是不是树的问题。
我的看法是:二叉树不是树,最为关键的一点,树不可以为空,二叉树可以空,大家看上面的定义就可以知道。
(纯粹个人观点,因为我在网上找了好久两种说法都有,我是比较偏向二叉树不是树的,如果我看的定义都没错的话)