深度学习入门笔记（六）：浅层神经网络

专栏——深度学习入门笔记

声明

1）该文章整理自网上的大牛和机器学习专家无私奉献的资料，具体引用的资料请看参考文献。
2）本文仅供学术交流，非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益，还望海涵，并联系博主删除。
3）博主才疏学浅，文中如有不当之处，请各位指出，共同进步，谢谢。
4）此属于第一版本，若有错误，还需继续修正与增删。还望大家多多指点。大家都共享一点点，一起为祖国科研的推进添砖加瓦。

深度学习入门笔记（六）：浅层神经网络

1 、神经网络概述

关于神经网络的概述，具体的可以看这个博客——大话卷积神经网络CNN（干货满满），我在其中详细的介绍了 人类视觉原理、神经网络、卷积神经网络的定义和相关网络结构基础，还有 应用 和 关于深度学习的本质的探讨，如果你需要 学习资源 也可以在博客中找一下，这里就不详细介绍了。

什么是浅层神经网络呢？

看了上面提到的博客，你应该知道相关概念了，浅层神经网络其实就是一个单隐层神经网络！！！

2、激活函数和激活函数的导数

使用一个神经网络时，需要决定使用哪种激活函数用隐藏层上？哪种用在输出节点上？不同的激活函数的效果是不一样的。下面将介绍一下常用的激活函数：

• sigmoid 函数

函数图像和导数图像如下：

公式如下：

$$a=\sigma (z)=\frac{1}{{1+e}^{-z}}$$

导数公式如下：

$$\frac{d}{dz}g(z)=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=g(z)(1-g(z))$$

如果没有非线性的激活函数，再多的神经网络只是计算线性函数，或者叫恒等激励函数。sigmoid 函数是使用比较多的一个激活函数。

• tanh 函数

函数图像和导数图像如下：

公式如下：

$$a=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$

导数公式如下：

$$\frac{d}{dz}g(z)=1-(tanh(z){)}^2$$

事实上，tanh 是 sigmoid 的向下平移和伸缩后的结果。对它进行了变形后，穿过了$(0,0)$点，并且值域介于 +1 和 -1 之间。

所以效果总是优于 sigmoid 函数。因为函数值域在 -1 和 +1 的激活函数，其均值是更接近零均值的。在训练一个算法模型时，如果使用 tanh 函数代替 sigmoid 函数中心化数据，使得数据的平均值更接近0而不是0.5。但是也有例外的情况，有时对隐藏层使用 tanh 激活函数，而输出层使用 sigmoid 函数，效果会更好。

小结：

sigmoid 函数和 tanh 函数两者共同的缺点是，在未经过激活函数的输出特别大或者特别小的情况下，会导致导数的梯度或者函数的斜率变得特别小，最后就会接近于0，导致降低梯度下降的速度。

• ReLu 函数

在机器学习另一个很流行的函数是：修正线性单元的函数（ReLu）。

函数图像和导数图像如下：

公式如下：

$$a=max(0,z)$$

导数公式如下：

$$g(z{)}^{{}^{\prime }}=\{\begin{array}{ll}0& \text{if z < 0}\\ 1& \text{if z > 0}\\ undefined& \text{if z = 0}\end{array}$$

当 $z$ 是正值的情况下，导数恒等于1，当 $z$ 是负值的时候，导数恒等于0。Relu 的一个优点是当 $z$ 是负值的时候，导数等于0，当 $z$ 是正值的时候，导数等于1。这样在梯度下降时就不会受 梯度爆炸或者梯度消失 的影响了。

详见博客——深度学习100问之深入理解Vanishing/Exploding Gradient（梯度消失/爆炸）

一些选择激活函数的经验法则：
如果输出是0、1值（二分类问题），则输出层选择 sigmoid 函数，然后其它的所有单元都选择 Relu 函数。这是很多激活函数的默认选择，如果在隐藏层上不确定使用哪个激活函数，那么通常会使用 Relu 激活函数。有时，也会使用 tanh 激活函数。

• Leaky Relu 函数

这里也有另一个版本的 Relu 被称为 Leaky Relu。

函数图像和导数图像如下：

与 ReLU 类似，公式如下：

$$g(z)=\max (0.01z,z)$$

导数公式如下：

$$g(z{)}^{{}^{\prime }}=\{\begin{array}{ll}0.01& \text{if z < 0}\\ 1& \text{if z > 0}\\ undefined& \text{if z = 0}\end{array}$$

当 $z$ 是负值时，这个函数的值不是等于0，而是轻微的倾斜。这个函数通常比 Relu 激活函数效果要好，尽管在实际中 Leaky ReLu 使用的并不多。

RELU 系列的两个激活函数的优点是：

• 第一，在未经过激活函数的输出的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于0，在程序实现就是一个 if-else 语句，而 sigmoid 函数需要进行浮点四则运算，在实践中，使用 ReLu 激活函数神经网络通常会比使用 sigmoid 或者 tanh 激活函数学习的更快。

• 第二，sigmoid 和 tanh 函数的导数在正负饱和区的梯度都会接近于0，这会造成梯度弥散，而 Relu 和 Leaky ReLu 函数大于0部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，Relu 进入负半区的时候，梯度为0，神经元此时不会训练，产生所谓的 稀疏性，而 Leaky ReLu 不会有这问题。但 ReLu 的梯度一半都是0，有足够的隐藏层使得未经过激活函数的输出值大于0，所以对大多数的训练数据来说学习过程仍然可以很快。)

最后简单介绍完了常用的激活函数之后，来快速概括一下。

• sigmoid 激活函数：除了输出层是一个二分类问题基本上不会用 sigmoid。

• tanh 激活函数：tanh 是非常优秀的，几乎适合所有场合。

• ReLu 激活函数：最常用的默认激活函数。如果不确定用哪个激活函数，就先使用 ReLu。

很多人在编写神经网络的时候，经常遇到一个问题是，有很多个选择：隐藏层单元的个数、激活函数的种类、初始化权值的方式、等等……这些选择想得到一个比较好的指导原则是挺困难的，所以其实更多的是经验，这也是深度学习被人称为经验主义学科和被人诟病的地方，更像是一种炼丹术，是不是？

你可能会看到好多博客，文章，或者哪一个工业界大佬或者学术界大佬说过，哪一种用的多，哪一种更好用。但是，你的神经网络的结构，以及需要解决问题的特殊性，是很难提前知道选择哪些效果更好的，或者没办法确定别人的经验和结论是不是对你同样有效。

所以通常的建议是：如果不确定哪一个激活函数效果更好，可以把它们都试试，然后在验证集或者测试集上进行评价，这样如果看到哪一种的表现明显更好一些，就在你的网络中使用它！！！

3、为什么需要非线性激活函数？

为什么神经网络需要非线性激活函数？

首先是事实证明了，要让神经网络能够计算出有趣的函数，必须使用非线性激活函数。但是这么说太不科学了，现在来证明一下，证明过程如下：

$a^{[1]}=g(z^{[1]})$，这是神经网络正向传播的方程，之前我们学过的，你还记得不？不记得去翻翻 深度学习入门笔记（二）：神经网络基础。

现在去掉函数 $g$，也就是去掉激活函数，然后令 $a^{[1]}=z^{[1]}$，或者也可以直接令 $g(z^{[1]})=z^{[1]}$，这个有时被叫做 线性激活函数（更学术点的名字是 恒等激励函数，因为它们就是把输入值直接输出）。

因为：

(1) $a^{[1]}=z^{[1]}=W^{[1]}x+b^{[1]}$

(2) $a^{[2]}=z^{[2]}=W^{[2]}{a}^{[1]}+b^{[2]}$

将式子(1)代入式子(2)中，则得到：

(3) $a^{[2]}=z^{[2]}=W^{[2]}(W^{[1]}x+b^{[1]})+b^{[2]}=W^{[2]}{W}^{[1]}x+W^{[2]}{b}^{[1]}+b^{[2]}=(W^{[2]}{W}^{[1]})x+(W^{[2]}{b}^{[1]}+b^{[2]})$

然后简化多项式，你可以发现两个括号里的式子都可以简化，可得：

(4) $a^{[2]}=z^{[2]}=W^{{}^{\prime }}x+b^{{}^{\prime }}$

小结：如果使用 线性激活函数 或者叫 恒等激励函数，那么神经网络只是把输入线性组合再输出。

之后我们会学到 深度网络，什么是 深度网络？顾名思义，就是有很多层（很多隐藏层）的神经网络。然而，上面的证明告诉我们，如果使用线性激活函数或者不使用激活函数，那么无论你的神经网络有多少层，一直在做的也只是计算线性函数，都可以用 $a^{[2]}=z^{[2]}=W^{{}^{\prime }}x+b^{{}^{\prime }}$ 表示，还不如直接去掉全部隐藏层，反正也没啥用。。。

总之，不能在隐藏层用线性激活函数，相反你可以用 ReLU 或者 tanh 或者 leaky ReLU 或者其他的非线性激活函数，唯一可以用线性激活函数的通常就是输出层。

4、神经网络的梯度下降

我们这一次讲的浅层神经网络——单隐层神经网络，会有 $W^{[1]}$，$b^{[1]}$，$W^{[2]}$，$b^{[2]}$ 这些个参数，还有个 $n_x$ 表示输入特征的个数，$n^{[1]}$ 表示隐藏单元个数，$n^{[2]}$ 表示输出单元个数。

好了，这就是全部的符号参数了。那么具体参数的维度如下：

• 矩阵 $W^{[1]}$ 的维度就是($n^{[1]},n^{[0]}$)，$b^{[1]}$ 就是 $n^{[1]}$维向量，可以写成 $(n^{[1]},1)$，就是一个的列向量。

• 矩阵 $W^{[2]}$ 的维度就是($n^{[2]},n^{[1]}$)，$b^{[2]}$ 的维度和 $b^{[1]}$ 一样，就是写成 $(n^{[2]},1)$。

此外，还有一个神经网络的 代价函数（Cost function），在之前的博客——深度学习入门笔记（二）：神经网络基础 中讲过，不过是基于逻辑回归的。假设现在是在做二分类任务，那么代价函数等于：

$$J(W^{[1]},b^{[1]},W^{[2]},b^{[2]})=\frac{1}{m}\sum _{i=1}^{m}L(\hat{y},y)$$

训练参数之后，需要做梯度下降，然后进行参数更新，进而网络优化。所以，每次梯度下降都会循环，并且计算以下的值，也就是网络的输出：

$${\hat{y}}^{(i)}(i=1,2,\dots ,m)$$

• 前向传播（forward propagation） 方程如下（之前讲过）：

(1) $z^{[1]}=W^{[1]}x+b^{[1]}$

(2) $a^{[1]}=\sigma (z^{[1]})$

(3) $z^{[2]}=W^{[2]}{a}^{[1]}+b^{[2]}$

(4) $a^{[2]}=g^{[2]}(z^{[z]})=\sigma (z^{[2]})$

• 反向传播（back propagation） 方程如下:

(1) $d{z}^{[2]}=A^{[2]}-Y,Y=\left[\begin{array}{cccc}{y}^{[1]}& y^{[2]}& \cdots & y^{[m]}\end{array}\right]$

(2) $d{W}^{[2]}=\frac{1}{m}d{z}^{[2]}{A}^{[1]T}$

(3) $\mathrm{d}{b}^{[2]}=\frac{1}{m}np.sum(d{z}^{[2]},axis=1,keepdims=True)$

(4) $d{z}^{[1]}=\underset{(n^{[1]},m)}{W^{[2]T}\mathrm{d}{z}^{[2]}}\ast \underset{activationfunctionofhiddenlayer}{{g^{[1]}}^{{}^{\prime }}}\ast \underset{(n^{[1]},m)}{(z^{[1]})}$

(5) $d{W}^{[1]}=\frac{1}{m}d{z}^{[1]}{x}^T$

(6) $\underset{(n^{[1]},1)}{d{b}^{[1]}}=\frac{1}{m}np.sum(d{z}^{[1]},axis=1,keepdims=True)$

注：反向传播的这些公式都是针对所有样本，进行过向量化的（深度学习入门笔记（四）：向量化）。

其中，$Y$ 是 $1\times m$ 的矩阵；这里 np.sum 是 python 的 numpy 命令，axis=1 表示水平相加求和，keepdims 是防止 python 输出那些古怪的秩数 $(n,)$，加上这个确保阵矩阵 $d{b}^{[2]}$ 这个向量的输出的维度为 $(n,1)$ 这样标准的形式。

编程操作看这个博客——深度学习入门笔记（五）：神经网络的编程基础。

• 参数更新 方程如下：

(1) $d{W}^{[1]}=\frac{dJ}{d{W}^{[1]}},d{b}^{[1]}=\frac{dJ}{d{b}^{[1]}}$

(1) $d{W}^{[2]}=\frac{dJ}{d{W}^{[2]}},d{b}^{[2]}=\frac{dJ}{d{b}^{[2]}}$

其中 $W^{[1]}⟹W^{[1]}-ad{W}^{[1]}，b^{[1]}⟹b^{[1]}-ad{b}^{[1]}$，$W^{[2]}⟹W^{[2]}-\alpha \mathrm{d}{W}^{[2]}，b^{[2]}⟹b^{[2]}-\alpha \mathrm{d}{b}^{[2]}$。

如果你跟着咱们系列下来的话（深度学习入门笔记），应该发现了到目前为止，计算的都和 Logistic 回归（深度学习入门笔记（二）：神经网络基础）十分的相似，但当你开始 计算 反向传播的时候，你会发现，是需要计算隐藏层和输出层激活函数的导数的，在这里（二元分类）使用的是 sigmoid 函数。

如果你想认真的推导一遍反向传播，深入理解反向传播的话，欢迎看一下这个博客——深度学习100问之深入理解Back Propagation（反向传播），只要你跟着推导一遍，反向传播基本没什么大问题了。或者如果你觉得自己数学不太好的话，也可以和许多成功的深度学习从业者一样直接实现这个算法，不去了解其中的知识，这就是深度学习相较于机器学习最大的优势，我猜是的。

5、随机初始化

当训练神经网络时，权重随机初始化 是很重要的，简单来说，参数初始化 就是 决定梯度下降中的起始点。对于逻辑回归，把权重初始化为0当然也是可以的，但是对于一个神经网络，如果权重或者参数都初始化为0，那么梯度下降将不会起作用。你一定想问为什么？

慢慢来看，假设现在有两个输入特征，即 $n^{[0]}=2$，2个隐藏层单元，即 $n^{[1]}$ 等于2，因此与一个隐藏层相关的矩阵，或者说 $W^{[1]}$ 就是一个 2*2 的矩阵。我们再假设，在权重随机初始化的时候，把它初始化为 0 的 2*2 矩阵，$b^{[1]}$ 也等于 $[00{]}^T$（把偏置项 $b$ 初始化为0是合理的），但是把 $w$ 初始化为 0 就有问题了。你会发现，如果按照这样进行参数初始化的话，总是发现 $a_1^{[1]}$ 和 $a_2^{[1]}$ 相等，这两个激活单元就会一样了！！！为什么会这样呢？

因为在反向传播时，两个隐含单元计算的是相同的函数，都是来自 $a_1^{[2]}$ 的梯度变化，也就是 ${\text{dz}}_1^{[1]}$ 和 ${\text{dz}}_2^{[1]}$ 是一样的，由 $W^{[1]}=W^{[1]}-adW$ 可得 $W^{[1]}=adW$，学习率 $a$ 一样，梯度变化 $dW$ 一样，这样更新后的输出权值也会一模一样，由此 $W^{[2]}$ 也等于 $[00]$。

你可能觉得这也没啥啊，大惊小怪的，但是如果这样初始化这整个神经网络的话，那么这两个隐含单元就完全一样了，因此它们两个完全对称，也就意味着计算同样的函数，并且肯定的是最终经过每次训练的迭代，这两个隐含单元仍然是同一个函数，令人困惑。

由此可以推导，由于隐含单元计算的是同一个函数，所有的隐含单元对输出单元有同样的影响。一次迭代后，同样的表达式结果仍然是相同的，即 隐含单元仍是对称的。那么两次、三次、无论多少次迭代，不管网络训练多长时间，隐含单元仍然计算的是同样的函数。因此这种情况下超过1个隐含单元也没什么意义，因为计算的是同样的东西。当然无论是多大的网络，比如有3个特征，还是有相当多的隐含单元。

那么这个问题的解决方法是什么？其实很简单，就是 随机初始化参数。

你应该这么做：把 $W^{[1]}$ 设为 np.random.randn(2,2)(生成标准正态分布)，通常再乘上一个较小的数，比如 0.01，这样就把它初始化为一个很小的随机数。然后 $b$ 本来就没有这个对称的问题（叫做symmetry breaking problem），所以可以把 $b$ 初始化为0，因为只要随机初始化 $W$，就有不同的隐含单元计算不同的东西，就不会有 symmetry breaking 问题了。相似地，对于 $W^{[2]}$ 也随机初始化，$b^{[2]}$ 可以初始化为0。

举一个随机初始化的例子，比如：

$$W^{[1]}=np.random.randn(2,2)\ast 0.01,b^{[1]}=np.zeros((2,1))$$

$$W^{[2]}=np.random.randn(2,2)\ast 0.01,b^{[2]}=0$$

你也许会疑惑，这个常数从哪里来？为什么是0.01，而不是100或者1000？

这是因为我们 通常倾向于初始化为很小的随机数。

这么想，如果你用 tanh 或者 sigmoid 激活函数，或者说只在输出层有一个 sigmoid 激活函数，这种情况下，如果（数值）波动太大，在计算激活值时 $z^{[1]}=W^{[1]}x+b^{[1]},a^{[1]}=\sigma (z^{[1]})=g^{[1]}(z^{[1]})$，如果 $W$ 很大，$z$ 就会很大或者很小，这种情况下很可能停在 tanh / sigmoid 函数的平坦的地方（甚至在训练刚刚开始的时候），而这些平坦的地方对应导数函数图像中梯度很小的地方，也就意味着梯度下降会很慢（因为梯度小），因此学习也就很慢，这显然是不好的。

sigmoid 函数图像和导数函数图像：

tanh 函数图像和导数函数图像：

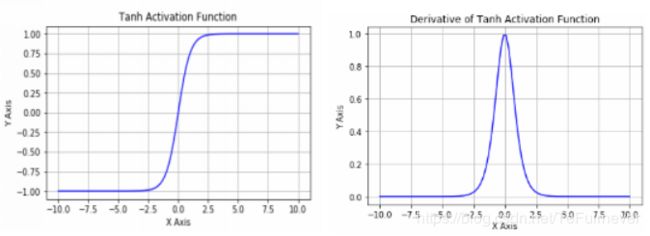
如果你没有使用 sigmoid / tanh 激活函数在整个的神经网络里，就不成问题。但如果做二分类并且输出单元是 Sigmoid 函数，那么你一定不会想让你的初始参数太大，因此这就是为什么乘上 0.01 或者其他一些小数是合理的尝试,对 $w^{[2]}$ 也是一样。

关于浅层神经网络的代码，可以手撕一下，欢迎看一下这个博客——深度学习之手撕神经网络代码（基于numpy）。

推荐阅读

• 深度学习入门笔记（一）：深度学习引言
• 深度学习入门笔记（二）：神经网络基础
• 深度学习入门笔记（三）：求导和计算图
• 深度学习入门笔记（四）：向量化
• 深度学习入门笔记（五）：神经网络的编程基础
• 深度学习入门笔记（六）：浅层神经网络
• 深度学习入门笔记（七）：深层神经网络
• 深度学习入门笔记（八）：深层网络的原理
• 深度学习入门笔记（九）：深度学习数据处理
• 深度学习入门笔记（十）：正则化
• 深度学习入门笔记（十一）：深度学习数据读取
• 深度学习入门笔记（十二）：权重初始化

参考文章

• 吴恩达——《神经网络和深度学习》视频课程