前缀和与差分

前缀和

---

其实可以把它理解为数学上的数列的前n项和（对于一个一维数组的前缀和）。

我们定义对于一个数组$a[]$的前缀和数组$s$，$s[i] = a[1]+a[2]+...+a[i]$.

二维前缀和与一维前缀和类似，设$s[i][j]$表示所有$a[i{}'][j{}']$的和。$(1\leq i{}'\leq i,1\leq j{}'\leq j)$

有一点像“矩形的面积”那样，把一整块区域的值都加起来。

前缀和的用途

一般用来求区间和

对于一维情况

现在给出一个数列$a$，要求回答$m$次询问，每次询问下标$l$到$r$的和

朴素的做法显然是对于每次询问都执行一次相加操作，然后输出结果。这样做是正确的，但是当$m$过大时就会导致计算次数过多而有可能超时。
超时的原因一目了然，重复计算。那么我们应该怎么改进这个方法呢？

想象一下，我们如果先提前算好了每一个位置的前缀和，然后用$s[r]-s[l-1]$，结果不就是我们这次询问的答案吗？这样便会使计算量大大减小。

对于二维的区间和，也是类似的

 

我们借助这个图片研究一下。假设在这个矩阵（二维数组）中，我们要求和的是上图中红色区域。现在我们已经预处理出了所有点的前缀和，现在给定两个点$(x1,y1)$，$(x2,y2)$，我们要求 以这两个点连线为对角线的一个子矩阵的数值之和。暴力做法直接挨个加这个我就不再多说了，反正早晚都得$TLE$，我们重点考虑用前缀和的快速做法。

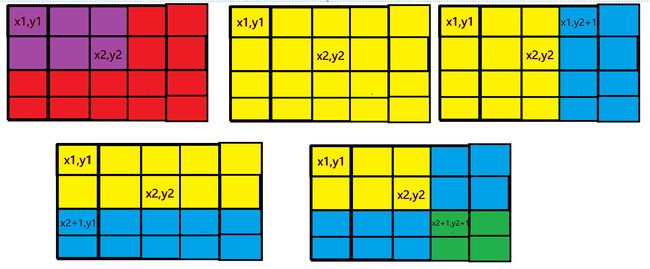
首先我们可以把$s[x2][y2]$求出来，它代表整个大矩形的前缀和，然后我们分别减去它左边多出来的一块的前缀和和下边多出来一块的前缀和，这样就是最终答案了？

不是！这不是最终答案。可以发现，在我们剪掉这两个多出的区域时，下边的一小块被减了两次，但减两次显然是不合理的，我们应该加回来。

所以对于一次的查询答案$ans$应该等于$s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]$

这个二维前缀和也称差分序列。

 

差分

---

对于一维情况

给定一个长度为$n$的数列a，有$q$个操作，每次操作给定$l,r,x$表示$[l,r]$区间所有的数都加上$x$。并求修改后的序列$a$。

暴力做法显然会$TLE$，我们考虑用差分的做法。

之所以叫做差分，是因为我们需要维护的数据是“相邻两个数之差”。

差分数组不仅仅是一个优秀的数据结构，还是一种很好的思想

差分数组的功能是修改区间，查询点。修改区间的时间复杂度是$O(1)$，查询点的时间复杂度为$O(n)$

我们这里要根据数据范围灵活选取方法，不要拘泥于差分数组

void update(int l,int r,int x)
{
    c[l]+=x;
    c[r+1]-=x;
}

以上是修改区间操作，$l$位置加上修改量，$r+1$位置减去修改量，这样整个区间的元素就相当于修改了

int sum(int x)
{
    int ans=0;
    for(int i=1;i<=x;i++)
        ans+=c[i];
    return ans;
}

刚才修改方便了不少，但是查询的时候就需要全部都加一遍了

还有就是预处理的时候

c[1]=a[1];
for(int i=2;i<=n;i++)
    c[i]=a[i]-a[i-1];

 

对于二维的情况

给定一个$n\ast m$的矩阵，要求支持操作$add(x1,y1,x2,y2,a)$，表示对于以$(x1,y1)$为左上角，$(x2,y2)$为右下角的矩形区域，每个元素都加上$a$。要求修改后的矩阵。

类比二维前缀和和一维差分，可以简单推测出二维差分的公式

　　$c[i][j]=a[i][j]−a[i−1][j]−a[i][j−1]+a[i−1][j−1]$

我们再代入检验，即将左上角的矩阵差分求和，正好得到了这个数

如果我们要在左上角是$(x1,y1)$,右下角是$(x2,y2)$的矩形区间每个值都$+a$

 

 在我们要的区间开始位置$(x1,y1)$处$+a$，根据前缀和的性质，那么它影响的就是整个黄色部分，多影响了两个蓝色部分，所以在两个蓝色部分$-a$消除$+a$的影响，而两个蓝色部分重叠的绿色部分多受了个$-a$的影响，所以绿色部分$+a$消除影响。

最后$(x,y)$位置上的数值就是$c$数组在$(x,y)$位置的前缀和。

 

---

参考资料：
https://www.cnblogs.com/OIerShawnZhou/p/7348088.html

https://www.cnblogs.com/LMCC1108/p/10753451.html

https://www.cnblogs.com/aininot260/p/9304521.html

https://zhuanlan.zhihu.com/p/33336151

https://www.cnblogs.com/waterflower/p/11100774.html

https://www.cnblogs.com/zwx7616/p/10735821.html