Python计算机视觉编程第五章——多视图几何

多视图几何

几何计算机视觉把复杂的数学（尤其是射影几何等）引入到计算机视觉的研究中，形成了所谓的“多视图几何”。多视图几何为理解和形式化多视图成像几何奠定了坚实的理论基础，使得十几年前被认为无法解或难以解的问题得以求解，甚至能得到十分漂亮的结果。其最重要的特点是“未标定”方法，即没有必要已知或必须计算摄像机内参数，就可以达到计算机视觉的基本目的。

（一）外极几何

外极几何是研究两幅图像之间存在的几何。它和场景结构无关，只依赖于摄像机的内外参数。研究这种几何可以用在图像匹配、三维重建方面。

基本概念：

基线：  连接两个摄像机光点$O(O^{\prime })$的直线。
外极点：  基线与像平面的交点。
外极平面：  过基线的平面。
外极线：  对极平面与图像平面的交线。
基本矩阵$F$：  对应点对之间的约束$m^{{}^{\prime }T}Fm=0$

数学表达：
光心：  $O={\left[\begin{array}{cccc}0& 0& 0& 1\end{array}\right]}^{\tau }$     $O^{{}^{\prime }}={\left[\begin{array}{cc}-R^{\tau }t& 1\end{array}\right]}^{\tau }$

基本矩阵$F$:    $F=K^{{}^{\prime }-T}[t]xR{K}^{-1}$是秩为2的3x3矩阵，自由度为7。

外极点：  $e=P{O}^{{}^{\prime }}=P{\left[\begin{array}{cc}-R^{\tau }t& 1\end{array}\right]}^T\approx K{R}^{\tau }t$
                $e^{{}^{\prime }}=P^{{}^{\prime }}O=P^{{}^{\prime }}{\left[\begin{array}{cccc}0& 0& 0& 1\end{array}\right]}^T=K^{{}^{\prime }}t$

外极线：  $l=e\times m$
                $l^{{}^{\prime }}=e^{{}^{\prime }}\times m^{{}^{\prime }}$
本质矩阵$E$:   $E=[t{]}_{x}R$ 是秩为$2$的$3\times 3$矩阵，自由度为$5$。
对象之间的关系：  $l=F^T{m}^{{}^{\prime }}$      $l^{{}^{\prime }}=Fm$
                               $Fe=0$          $e=F^{{}^{\prime }T}F=0$
                               $e^{{}^{\prime }T}F=0$      $F=K^{{}^{\prime }-T}E{K}^{-1}$

在两幅图像之间，基本矩阵将点m映射为对应的对极线，将对极点映射为0.不能提供对应点间的一一对应。

基本矩阵的代数推导:

空间中一点$M={\left[\begin{array}{cc}X& 1\end{array}\right]}^T$在两幅图像上的成像分别为：

$sm=P{\left[\begin{array}{cc}X& 1\end{array}\right]}^T=KX$
$s^{’}{m}^{{}^{\prime }}=P^{{}^{\prime }}\left[\begin{array}{cc}X& 1\end{array}\right]=K^{{}^{\prime }}RX+K^{{}^{\prime }}t$

极点：$e^{{}^{\prime }}=P^{{}^{\prime }}C=P^{{}^{\prime }}{\left[\begin{array}{cccc}0& 0& 0& 1\end{array}\right]}^T=K^{{}^{\prime }}t$

极线：$l^{{}^{\prime }}={\left[e^{{}^{\prime }}\right]}_x{m}^{{}^{\prime }}={\left[K^{{}^{\prime }}t\right]}_x\left[K^{{}^{\prime }}RX+K^{{}^{\prime }}t\right]=K^{{}^{\prime }-T}{\left[t\right]}_{x}R{K}^{-1}m=Fm$

因此：$m^{{}^{\prime }T}{l}^{{}^{\prime }}=m^{{}^{\prime }T}{K}^{{}^{\prime }-T}{\left[t\right]}_{x}R{K}^{-1}m=m^{{}^{\prime }T}Fm=0$

1.1 一个简单的数据集

在接下来的几节中，需要一个带有图像点、三维点和照相机参数矩阵的数据集。 这里使用一个牛津多视图数据集；从http://www.robots.ox.ac.uk/~vgg/data/datamview.html 可以下载 Merton1 数据的压缩文件。下面的脚本可以加载 Merton1 的数据：

编写代码：

# -*- coding: utf-8 -*-
from pylab import *
import camera
from PIL import Image
# 载入一些图像
im1 = array(Image.open('D:\\Python\\chapter5\\girl2.jpg'))
im2 = array(Image.open('D:\\Python\\chapter5\\girl3.jpg'))
# 载入每个视图的二维点到列表中
points2D = [loadtxt('D:\\Python\\chapter5\\00'+str(i+1)+'.corners').T for i in range(3)]
# 载入三维点
points3D = loadtxt('D:\\Python\\chapter5\\p3d').T
# 载入对应
corr = genfromtxt('D:\\Python\\chapter5\\nview-corners')
# 载入照相机矩阵到 Camera 对象列表中
P = [camera.Camera(loadtxt('D:\\Python\\chapter5\\00'+str(i+1)+'.P')) for i in range(3)]

# -*- coding: utf-8 -*-
execfile('aaaaa.py')
# 将三维点转换成齐次坐标表示，并投影
X = vstack( (points3D,ones(points3D.shape[1])) )
x = P[0].project(X)
# 在视图 1 中绘制点
figure()
imshow(im1)
plot(points2D[0][0],points2D[0][1],'*')
axis('off')
figure()
imshow(im1)
plot(x[0],x[1],'r.')
axis('off')
show()

代码运行效果如下：

a. 视图1与图像点

b. 视图1与投影的三维点

分析：

上面的程序会加载前两个图像（共三个）、三个视图中的所有图像特征点 1、对应不同视图图像点重建后的三维点以及照相机参数矩阵（使用上一章的 Camera 类）。这里使用 loadtxt() 函数读取文本文件到 NumPy 数组中。因为并不是所有的点都可见，或都能够成功匹配到所有的视图，所以对应数据里包含了缺失的数据。加载对应数据时需要考虑这一点。genfromtxt() 函数通过将缺失的数值（在文件中用 * 表示）填充为 -1 来解决这个问题。将上面的代码保存到一个文件，例如 aaaaa.py ，然后使用命令 execfile() 可 以很方便地运行上面的脚本，从而获取所有的数据，将三维的点投影到一个视图，然后和观测到的图像点比较，上面的代码绘制出第一个视图以及该视图中的图像点。为比较方便，投影后的点绘制在另一张图上。如果仔细观察，会发现第二幅图比第一幅图多一些点。这些多出的点是从视图 2 和视图 3 重建出来的，而不在视图 1 中。

1.2 用 Matplotlib 绘制三维数据

为了可视化三维重建结果，我们需要绘制出三维图像。Matplotlib 中的 mplot3d 工具 包可以方便地绘制出三维点、线、等轮廓线、表面以及其他基本图形组件，还可以 通过图像窗口控件实现三维旋转和缩放。

编写代码：

# -*- coding: utf-8 -*-
from pylab import *
from mpl_toolkits.mplot3d import axes3d
fig = figure()
ax = fig.gca(projection="3d")
# 生成三维样本点
X,Y,Z = axes3d.get_test_data(0.25)
# 在三维中绘制点
ax.plot(X.flatten(),Y.flatten(),Z.flatten(),'o')
show()

代码运行效果如下：

get_test_data() 函数在 x, y 空间按照设定的空间间隔参数来产生均匀的采样点。压平这些网格，会产生三列数据点，然后我们可以将其输入 plot() 函数。这样，我们就可以在立体表面上画出三维点。

现在通过画出 Merton 样本数据来观察三维点的效果：

编写代码：

# -*- coding: utf-8 -*-
from pylab import *
from mpl_toolkits.mplot3d import axes3d
fig = figure()
ax = fig.gca(projection="3d")
ax.plot(points3D[0],points3D[1],points3D[2],'k.')
show()

代码运行效果如下：

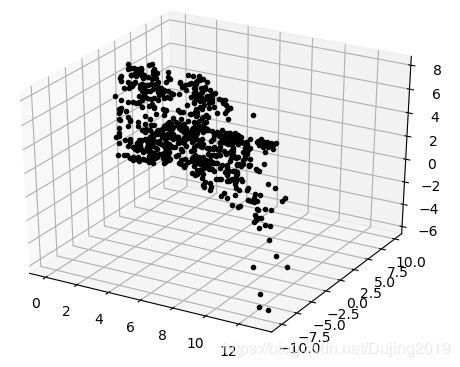
上图是三个不同视图中的三维图像点。图像窗口和控制界面外观效果像加上三维旋转工具的标准画图窗口。

1.3 计算 F：八点法

8点算法是计算基本矩阵（两幅图像之间的约束关系使用代数的方式表示出来即为基本矩阵）的最简单的方法，它仅涉及构造并（最小二乘）解一个线性方程组，如果小心的话，它可以执行得非常好。8点算法成功的关键是在构造解的方程之前应对输入的数据认真进行适当的归一化。在形成8点算法的线性方程组之前，图像点的一个简单变换（平移或变尺度）将使这个问题的条件极大的改善，从而提高结果的稳定性，而且进行这种变换所增加的计算复杂性并不显著。

8点算法估计基本矩阵F的结果与图像点的坐标系有关。当图像数据有噪声，即对应点不精确时，由8点算法给出的基本矩阵$F$的解精度很低。

值得推荐的一种归一化方法是对每一幅图像作平移和缩放使得参考点的形心在坐标原点并且点到原点的$RMS$（均方根）距离等于根号$\sqrt{2}$。

给定n≥8组对应点{$\widehat{x_i}\leftrightarrow x_i^{{}^{\prime }}$}，确定基本矩阵$F$使得$x_i^{{}^{\prime }T}F{x}_i=0$

F的归一化8点算法：

1. 归一化：根据$\widehat{x_i}=T{x}_i$，$\widehat{x_i^{{}^{\prime }}}=T^{{}^{\prime }}{x}_i^{{}^{\prime }}$，变换图像坐标。其中$T$和$T^{{}^{\prime }}$是有平移和缩放组成的归一化变换。
2. 求解对应匹配$\widehat{x_i}\leftrightarrow x_i^{{}^{\prime }}$的基本矩阵${\hat{F}}^{\prime }$
   a. 线性解：用$\hat{A}$ 的最小奇异值的奇异矢量确定$\hat{F}$，其中$\hat{A}$由匹配$\widehat{x_i}\leftrightarrow x_i^{{}^{\prime }}$形成。
   b. 强迫约束：用SVD并以${\hat{F}}^{\prime }$代替$\hat{F}$， 使得det${\hat{F}}^{\prime }$=0。
3. 解除归一化：令$F=T^{{}^{\prime }T}{\hat{F}}^{{}^{\prime }}T$。矩阵F就是数据$\widehat{x_i}\leftrightarrow x_i^{{}^{\prime }}$的基本矩阵。

基本矩阵是由下述方程定义：

$$x^{{}^{\prime }T}Fx=0$$

其中$x\leftrightarrow x^{{}^{\prime }}$是两幅图像的任意一对匹配点。由于每一组点的匹配提供了计算$F$系数的一个线性方程，当给定至少7个点（3×3的齐次矩阵减去一个尺度，以及一个秩为2的约束），方程就可以计算出未知的$F$。我们记点的坐标为$x=(x,y,1{)}^T$，$x^{{}^{\prime }}=(x^{{}^{\prime }},y^{{}^{\prime }},1{)}^T$，则对应的方程为

$$\left[\begin{array}{ccc}x& y& 1\end{array}\right]\left[\begin{array}{ccc}{f}_{11}& f_{12}& f_{13}\\ f_{21}& f_{22}& f_{23}\\ f_{31}& f_{32}& f_{33}\end{array}\right]\left[\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\\ 1\end{array}\right]=0$$

展开后有
$$x^{{}^{\prime }}x{f}_{11}+x^{{}^{\prime }}y{f}_{12}+x^{{}^{\prime }}{f}_{13}+y^{{}^{\prime }}x{f}_{21}+y^{{}^{\prime }}x{f}_{21}+y^{{}^{\prime }}y{f}_{22}+y^{{}^{\prime }}{f}_{23}+x^{{}^{\prime }}x{f}_{11}+x^{{}^{\prime }}{f}_{31}+y^{{}^{\prime }}{f}_{32}+f33=0$$

把矩阵$F$写成列向量的形式，则有：

$$\left[\begin{array}{ccccccccc}{x}^{{}^{\prime }}x& x^{{}^{\prime }}y& x^{{}^{\prime }}& y^{{}^{\prime }}x& y^{{}^{\prime }}y& y^{{}^{\prime }}& x& y& 1\end{array}\right]f=0$$

给定n组点的集合，我们有如下方程：
$$Af=\left[\begin{array}{ccccccccc}{x}_1^{{}^{\prime }}{x}_1& x_1^{{}^{\prime }}{y}_1& x_1^{{}^{\prime }}& y_1^{{}^{\prime }}{x}_1& y_1^{{}^{\prime }}& x_1^{{}^{\prime }}& y_1^{{}^{\prime }}& 1& \\ .& .& .& .& .& .& .& .& \\ .& .& .& .& .& .& .& .& \\ .& .& .& .& .& .& .& .& \\ & & & & & & & & \\ x_n^{{}^{\prime }}{x}_n& x_n^{{}^{\prime }}{y}_n& x_n^{{}^{\prime }}& y_n^{{}^{\prime }}{x}_n& y_n^{{}^{\prime }}& x_n^{{}^{\prime }}& y_n^{{}^{\prime }}& 1& \end{array}\right]f=0$$

如果存在确定（非零）解，则系数矩阵$A$的秩最多是$8$。由于$F$是齐次矩阵，所以如果矩阵$A$的秩为$8$，则在差一个尺度因子的情况下解是唯一的。可以直接用线性算法解得。

如果由于点坐标存在噪声则矩阵$A$的秩可能大于$8$（也就是等于$9$，由于$A$是$n\times 9$的矩阵）。这时候就需要求最小二乘解，这里就可以用$SVD$来求解，$f$的解就是系数矩阵$A$最小奇异值对应的奇异向量，也就是$A$奇异值分解后$A=UD{V}^T$中矩阵$V$的最后一列矢量，这是在解矢量$f$在约束$\Vert f\Vert$下取$\Vert Af\Vert$最小的解。以上算法是解基本矩阵的基本方法，称为$8$点算法。

新建一个文件 sfm.py，写入下面8点法中最小化 $\Vert Af\Vert$的函数：

def compute_fundamental(x1, x2):
    """    Computes the fundamental matrix from corresponding points
        (x1,x2 3*n arrays) using the 8 point algorithm.
        Each row in the A matrix below is constructed as
        [x'*x, x'*y, x', y'*x, y'*y, y', x, y, 1] """

    n = x1.shape[1]
    if x2.shape[1] != n:
        raise ValueError("Number of points don't match.")

    # build matrix for equations
    A = zeros((n, 9))
    for i in range(n):
        A[i] = [x1[0, i] * x2[0, i], x1[0, i] * x2[1, i], x1[0, i] * x2[2, i],
                x1[1, i] * x2[0, i], x1[1, i] * x2[1, i], x1[1, i] * x2[2, i],
                x1[2, i] * x2[0, i], x1[2, i] * x2[1, i], x1[2, i] * x2[2, i]]

    # compute linear least square solution
    U, S, V = linalg.svd(A)
    F = V[-1].reshape(3, 3)

    # constrain F
    # make rank 2 by zeroing out last singular value
    U, S, V = linalg.svd(F)
    S[2] = 0
    F = dot(U, dot(diag(S), V))

    return F / F[2, 2]

由于上面算法得出的解可能秩不为 2（基础矩阵的秩小于等于 2），所以通过将最后一个奇异值置 0 来得到秩最接近 2 的 基础矩阵。这是个很有用的技巧。上面的函数忽略了一个重要的步骤：对图像坐标进行归一化，这可能会带来数值问题。这个会在后面加以解决。

实验步骤：

1. sift提取特征
2. RANSAC去除错误点匹配
3. 归一化8点算法估计基础矩阵

编写代码：

# -*- coding: utf-8 -*-
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
from PCV.geometry import camera
from PCV.geometry import homography
from PCV.geometry import sfm
from PCV.localdescriptors import sift
# -*- coding: utf-8 -*-

# Read features
# 载入图像，并计算特征
im1 = array(Image.open('D:\\Python\\chapter5\\crans_1_small.jpg'))
sift.process_image('D:\\Python\\chapter5\\crans_1_small.jpg', 'D:\\Python\\chapter5\\im1.sift')
l1, d1 = sift.read_features_from_file('D:\\Python\\chapter5\\im1.sift')

im2 = array(Image.open('D:\\Python\\chapter5\\crans_2_small.jpg'))
sift.process_image('D:\\Python\\chapter5\\crans_2_small.jpg', 'D:\\Python\\chapter5\\im2.sift')
l2, d2 = sift.read_features_from_file('D:\\Python\\chapter5\\im2.sift')

# 匹配特征
matches = sift.match_twosided(d1, d2)
ndx = matches.nonzero()[0]

# 使用齐次坐标表示，并使用 inv(K) 归一化
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)

x1n = x1.copy()
x2n = x2.copy()
print(len(ndx))

figure(figsize=(16,16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()

# Don't use K1, and K2

#def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
    """ Robust estimation of a fundamental matrix F from point
    correspondences using RANSAC (ransac.py from
    http://www.scipy.org/Cookbook/RANSAC).

    input: x1, x2 (3*n arrays) points in hom. coordinates. """

    from PCV.tools import ransac
    data = np.vstack((x1, x2))
    d = 20 # 20 is the original
    # compute F and return with inlier index
    F, ransac_data = ransac.ransac(data.T, model,
                                   8, maxiter, match_threshold, d, return_all=True)
    return F, ransac_data['inliers']

# find E through RANSAC
# 使用 RANSAC 方法估计 E
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-4)

print(len(x1n[0]))
print(len(inliers))

# 计算照相机矩阵（P2 是 4 个解的列表）
P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)

# triangulate inliers and remove points not in front of both cameras
X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)

# plot the projection of X
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)

figure()
imshow(im1)
gray()
plot(x1p[0], x1p[1], 'o')
#plot(x1[0], x1[1], 'r.')
axis('off')

figure()
imshow(im2)
gray()
plot(x2p[0], x2p[1], 'o')
#plot(x2[0], x2[1], 'r.')
axis('off')
show()

figure(figsize=(16, 16))
im3 = sift.appendimages(im1, im2)
im3 = vstack((im3, im3))

imshow(im3)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
    if (0<= x1p[0][i]0: #plot([locs1[i][0],locs2[m][0]+cols1],[locs1[i][1],locs2[m][1]],'c')
        x1=int(l1[i][0])
        y1=int(l1[i][1])
        x2=int(l2[int(m)][0])
        y2=int(l2[int(m)][1])
        # p1 = array([l1[i][0], l1[i][1], 1])
        # p2 = array([l2[m][0], l2[m][1], 1])
        p1 = array([x1, y1, 1])
        p2 = array([x2, y2, 1])
        # Use Sampson distance as error
        Fx1 = dot(F, p1)
        Fx2 = dot(F, p2)
        denom = Fx1[0]**2 + Fx1[1]**2 + Fx2[0]**2 + Fx2[1]**2
        e = (dot(p1.T, dot(F, p2)))**2 / denom
        x1e.append([p1[0], p1[1]])
        x2e.append([p2[0], p2[1]])
        ers.append(e)
x1e = array(x1e)
x2e = array(x2e)
ers = array(ers)

indices = np.argsort(ers)
x1s = x1e[indices]
x2s = x2e[indices]
ers = ers[indices]
x1s = x1s[:20]
x2s = x2s[:20]

figure(figsize=(16, 16))
im3 = sift.appendimages(im1, im2)
im3 = vstack((im3, im3))

imshow(im3)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1s)):
    if (0<= x1s[i][0]

sift特征点匹配方法，匹配效果为：



ransac算法结果为：


8点算法结果为：

基础矩阵：

[[ 2.65286282e-08 7.59820235e-06 -3.83459667e-03]
[-7.97876137e-06 -3.68074787e-07 4.91485874e-03]
[ 4.22012330e-03 -6.96718057e-03 1.00000000e+00]]

基础矩阵：

[[ 1.99147197e-07 -1.12968836e-07 -3.26762431e-04]
[-8.91591621e-10 -3.47702375e-07 -5.90332714e-04]
[-1.16017117e-03 1.26439607e-04 1.00000000e+00]]

1.4 外极点和外极线

本节开始提到过，外极点满足$F{e}_1=0$，因此可以通过计算 $F$ 的零空间来得到。把下面的函数添加到 sfm.py 中：

def compute_epipole(F):
    """ Computes the (right) epipole from a
        fundamental matrix F.
        (Use with F.T for left epipole.) """

    # return null space of F (Fx=0)
    U, S, V = linalg.svd(F)
    e = V[-1]
    return e / e[2]

如果想获得另一幅图像的外极点（对应左零空间的外极点），只需将$F$转置后输入上述函数即可。

我们可以在之前样本数据集的前两个视图上运行这两个函数：

# -*- coding: utf-8 -*-
execfile('aaaaa.py')
# -*- coding: utf-8 -*-
from pylab import *
from mpl_toolkits.mplot3d import axes3d
import sfm
# 在前两个视图中点的索引
ndx = (corr[:,0]>=0) & (corr[:,1]>=0)
# 获得坐标，并将其用齐次坐标表示
x1 = points2D[0][:,corr[ndx,0]]
x1 = vstack((x1,ones(x1.shape[1])))
x2 = points2D[1][:,corr[ndx,1]]
x2 = vstack((x2,ones(x2.shape[1])))
# 计算 F
F = sfm.compute_fundamental(x1,x2)
# 计算极点
e = sfm.compute_epipole(F)
# 绘制图像
figure()
imshow(im1)
# 分别绘制每条线，这样会绘制出很漂亮的颜色
for i in range(5):
    sfm.plot_epipolar_line(im1,F,x2[:,i],e,False)
axis('off')
figure()
imshow(im2)
# 分别绘制每个点，这样会绘制出和线同样的颜色
for i in range(5):
    plot(x2[0,i],x2[1,i],'o')
axis('off')
show()

代码运行效果如下：

分析：

首先，选择两幅图像的对应点，然后将它们转换为齐次坐标。这里的对应点是从一个文本文件中读取得到的 ; 由于缺失的数据在对应列表 corr 中为 -1，所以程序中有可能选取这些点。因此，上面的程序通过数组操作符 & 只选取了索引大于等于 0 的点。最后，在第一个视图中画出了前 5 个外极线，在第二个视图中画出了对应匹配点。这里我们主要借助 plot() 函数，将 x 轴的范围作为直线的参数，因此直线超出图像边界的部分会被截断。 如果 show_epipole 为真，外极点也会被画出来（如果输入参数中没有外极点，外极点会在程序中计算获得）。在两幅图中，用不同的颜色将点和相应的外极线对应起来。

（二）照相机和三维结构的计算

2.1 三角剖分

三角剖分：假设V是二维实数域上的有限点集，边$e$是由点集中的点作为端点构成的封闭线段，$E$为$e$的几何。那么该点集V的一个三角剖分$T=(V,E)$是一个平面图$G$，该平面图满足条件：

1. 除了端点，平面图中的边不包含点集中的任何点。
2. 没有相交边。
3. 平面图中所有的面都是三角面，且所有三角面的合集是散点集$V$的凸包。

给定照相机参数模型，图像点可以通过三角剖分来恢复出这些点的三维位置。

对于两个照相机 $P_1$ 和$P_2$ 的视图，三维实物点 $X$ 的投影点为 $x_1$ 和 $x_2$（这里用齐次坐标表示），照相机方程定义了下列关系：

$$\left[\begin{array}{ccc}{p}_1& -x_1& 0\\ p_2& 0& -x_2\end{array}\right]\left[\begin{array}{c}X\\ {\lambda }_1\\ {\lambda }_2\end{array}\right]=0$$

由于图像噪声、照相机参数误差和其他系统误差，上面的方程可能没有精确解。我们可以通过 SVD 算法来得到三维点的最小二乘估值。

下面的函数用于计算一个点对的最小二乘三角剖分，把它添加到 sfm.py 中：

def triangulate_point(x1, x2, P1, P2):
    """ Point pair triangulation from
        least squares solution. """

    M = zeros((6, 6))
    M[:3, :4] = P1
    M[3:, :4] = P2
    M[:3, 4] = -x1
    M[3:, 5] = -x2

    U, S, V = linalg.svd(M)
    X = V[-1, :4]

    return X / X[3]

最后一个特征向量的前 4 个值就是齐次坐标系下的对应三维坐标。可以增加下面的函数来实现多个点的三角剖分：

def triangulate(x1, x2, P1, P2):
    """    Two-view triangulation of points in
        x1,x2 (3*n homog. coordinates). """

    n = x1.shape[1]
    if x2.shape[1] != n:
        raise ValueError("Number of points don't match.")

    X = [triangulate_point(x1[:, i], x2[:, i], P1, P2) for i in range(n)]
    return array(X).T

这个函数的输入是两个图像点数组，输出为一个三维坐标数组。

编写代码来实现 Merton1 数据集上的三角剖分：

# -*- coding: utf-8 -*-
execfile('aaaaa.py')
# -*- coding: utf-8 -*-
from pylab import *
from mpl_toolkits.mplot3d import axes3d
import sfm
# 在前两个视图中点的索引
ndx = (corr[:,0]>=0) & (corr[:,1]>=0)
# 获得坐标，并将其用齐次坐标表示
x1 = points2D[0][:,corr[ndx,0]]
x1 = vstack((x1,ones(x1.shape[1])))
x2 = points2D[1][:,corr[ndx,1]]
x2 = vstack((x2,ones(x2.shape[1])))
Xtrue = points3D[:,ndx]
Xtrue = vstack( (Xtrue,ones(Xtrue.shape[1])) )
# 检查前三个点
Xest = sfm.triangulate(x1,x2,P[0].P,P[1].P)
print Xest[:,:3]
print Xtrue[:,:3]
# 绘制图像
fig = figure()
ax = fig.gca(projection='3d')
ax.plot(Xest[0],Xest[1],Xest[2],'ko')
ax.plot(Xtrue[0],Xtrue[1],Xtrue[2],'r.')
axis('equal')
show()

代码运行效果如下：

上面的代码首先利用前两个视图的信息来对图像点进行三角剖分，然后把前三个图像点的齐次坐标输出到控制台，最后绘制出恢复的最接近三维图像点。输出到控制台的信息如下：

[[ 1.03743725 1.56125273 1.40720017]
[-0.57574987 -0.55504127 -0.46523952]
[ 3.44173797 3.44249282 7.53176488]
[ 1. 1. 1. ]]
[[ 1.0378863 1.5606923 1.4071907 ]
[-0.54627892 -0.5211711 -0.46371818]
[ 3.4601538 3.4636809 7.5323397 ]
[ 1. 1. 1. ]]

算法估计出的三维图像点和实际图像点很接近。如上图所示，估计点和实际点可以很好地匹配。

2.2 由三维点计算照相机矩阵

如果已经知道了一些三维点及其图像投影，我们可以使用直接线性变换的方法来计算照相机矩阵$P$。本质上，这是三角剖分方法的逆问题，有时我们将其称为照相机反切法。利用该方法恢复照相机矩阵同样也是一个最小二乘问题。

每个三维点 $X_i$（齐次坐标系下）按照${\lambda }_i{x}_i=P{X}_i$投影到图像点 $x_i=\left[\begin{array}{ccc}{x}_i& y_i& 1\end{array}\right]$，相应的点满足下面的关系：
$$\left[\begin{array}{ccccccc}{X}_1^T& 0& 0& -x_1& 0& 0& ...\\ 0& X_1^T& 0& -y_1& 0& 0& ...\\ 0& 0& X_1^T& -1& 0& 0& ...\\ X_2^T& 0& 0& -x_2& 0& 0& ...\\ 0& X_2^T& 0& -y_2& 0& 0& ...\\ 0& & X_2^T& -1& 0& 0& ...\\ .& .& .& .& .& .& .\\ .& .& .& .& .& .& .\\ .& .& .& .& .& .& .\end{array}\right]\left[\begin{array}{c}{p}_1^T\\ p_2^T\\ p_3^T\\ {\lambda }_1\\ {\lambda }_2\\ .\\ .\\ .\end{array}\right]=0$$

其中 $p_1$、 $p_2$ 和 $p_3$ 是矩阵 P 的三行。上面的式子可以写得更紧凑，如下所示：

$$Mv=0$$
然后，可以使用 SVD 分解估计出照相机矩阵。利用上面讲述的矩阵操作，可以直接写出相应的代码。将下面的函数添加到 sfm.py 文件中：

def compute_P(x, X):
    """    Compute camera matrix from pairs of
        2D-3D correspondences (in homog. coordinates). """

    n = x.shape[1]
    if X.shape[1] != n:
        raise ValueError("Number of points don't match.")

    # create matrix for DLT solution
    M = zeros((3 * n, 12 + n))
    for i in range(n):
        M[3 * i, 0:4] = X[:, i]
        M[3 * i + 1, 4:8] = X[:, i]
        M[3 * i + 2, 8:12] = X[:, i]
        M[3 * i:3 * i + 3, i + 12] = -x[:, i]

    U, S, V = linalg.svd(M)

    return V[-1, :12].reshape((3, 4))

该函数的输入参数为图像点和三维点，构造出上述所示的 M 矩阵。最后一个特征向量的前 12 个元素是照相机矩阵的元素，经过重新排列成矩阵形状后返回。

下面，在我们的样本数据集上测试算法的性能。下面的代码会选出第一个视图中的 一些可见点（使用对应列表中缺失的数值），将它们转换为齐次坐标表示，然后估计照相机矩阵：

# -*- coding: utf-8 -*-
execfile('aaaaa.py')
# -*- coding: utf-8 -*-
from pylab import *
from mpl_toolkits.mplot3d import axes3d
import sfm,camera
corr = corr[:,0] # 视图 1
ndx3D = where(corr>=0)[0] # 丢失的数值为 -1
ndx2D = corr[ndx3D]
# 选取可见点，并用齐次坐标表示
x = points2D[0][:,ndx2D] # 视图 1
x = vstack( (x,ones(x.shape[1])) )
X = points3D[:,ndx3D]
X = vstack( (X,ones(X.shape[1])) )
# 估计 P
Pest = camera.Camera(sfm.compute_P(x,X))
# 比较！
print Pest.P / Pest.P[2,3]
print P[0].P / P[0].P[2, 3]
xest = Pest.project(X)
# 绘制图像
figure()
imshow(im1)
plot(x[0],x[1],'bo')
plot(xest[0],xest[1],'r.')
axis('off')
show()

代码运行效果如下：

为了检查照相机矩阵的正确性，将它们以归一化的格式（除以最后一个元素）打印到控制台。输出如下所示：

[[ 1.06520794e+00 -5.23431275e+01 2.06902749e+01 5.08729305e+02]
[-5.05773115e+01 -1.33243276e+01 -1.47388537e+01 4.79178838e+02]
[ 3.05121915e-03 -3.19264684e-02 -3.43703738e-02 1.00000000e+00]]
[[ 1.06774679e+00 -5.23448212e+01 2.06926980e+01 5.08764487e+02]
[-5.05834364e+01 -1.33201976e+01 -1.47406641e+01 4.79228998e+02]
[ 3.06792659e-03 -3.19008054e-02 -3.43665129e-02 1.00000000e+00]]

上面是估计出的照相机矩阵，下面是数据集的创建者计算出的照相机矩阵。可以看到，它们的元素几乎完全相同。使用估计出的照相机矩阵投影这些三维点， 然后绘制出投影后的结果。结果显示，真实点用圆圈表示，估计出的照相机投影点用点表示。

2.3 由基础矩阵计算照相机矩阵

在两个视图的场景中，照相机矩阵可以由基础矩阵恢复出来。假设第一个照相机矩阵归一化为$P1=[I|0]$，现在我们需要计算出第二个照相机矩阵$P_2$。研究分为两类， 未标定的情况和已标定的情况。

未标定的情况——投影重建
在没有任何照相机内参数知识的情况下，照相机矩阵只能通过射影变换恢复出来。 也就是说，如果利用照相机的信息来重建三维点，那么该重建只能由射影变换计算 出来（你可以得到整个投影场景中无畸变的重建点）。在这里，我们不考虑角度和距离。

因此，在无标定的情况下，第二个照相机矩阵可以使用一个（3×3）的射影变换得出。一个简单的方法是：

$$P_2=\left[S_{e}F|e\right]$$

其中，$e$ 是左极点，满足$e_T$F=0。

已标定的情况——度量重建
在已经标定的情况下，重建会保持欧式空间中的一些度量特性（除了全局的尺度参数）

给定标定矩阵 $K$，我们可以将它的逆 $K^{-1}$作用于图像点 $x_k=K^{-1}x$，因此，在新的图像坐标系下，照相机方程变为：
$$x_k=K^{-1}[R|t]X=[R|t]X$$

在新的图像坐标系下，点同样满足之前的基础矩阵方程：
$$x_{k2}^{T}F{x}_{k1}=0$$

在标定归一化的坐标系下，基础矩阵称为本质矩阵。为了区别为标定后的情况，以 及归一化了的图像坐标，我们通常将其记为 $E$，而非$F$。

从本质矩阵恢复出的照相机矩阵中存在度量关系，但有四个可能解。因为只有一个解产生位于两个照相机前的场景，所以我们可以轻松地从中选出来。

下面是计算这四个解的算法：

def compute_P_from_essential(E):
    """    Computes the second camera matrix (assuming P1 = [I 0])
        from an essential matrix. Output is a list of four
        possible camera matrices. """

    # make sure E is rank 2
    U, S, V = svd(E)
    if det(dot(U, V)) < 0:
        V = -V
    E = dot(U, dot(diag([1, 1, 0]), V))

    # create matrices (Hartley p 258)
    Z = skew([0, 0, -1])
    W = array([[0, -1, 0], [1, 0, 0], [0, 0, 1]])

    # return all four solutions
    P2 = [vstack((dot(U, dot(W, V)).T, U[:, 2])).T,
          vstack((dot(U, dot(W, V)).T, -U[:, 2])).T,
          vstack((dot(U, dot(W.T, V)).T, U[:, 2])).T,
          vstack((dot(U, dot(W.T, V)).T, -U[:, 2])).T]

    return P2

具体步骤：

1. 用SIFT算法实现两幅图像的特征点检测，找到对应的匹配点并绘制出来
2. 使用RANSAC方法估计最佳基础矩阵F，以及正确点的索引，求出不同图像对的基础矩阵
3. 由基础矩阵计算照相机矩阵
4. 从照相机矩阵的列表中，对正确点的三维点进行三角剖分，挑选出经过三角剖分后，在两个照相机前均含有最多场景点

编写代码：

# -*- coding: utf-8 -*-
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
from PCV.geometry import camera
import homography
from PCV.geometry import sfm
from PCV.localdescriptors import sift

camera = reload(camera)
homography = reload(homography)
sfm = reload(sfm)
sift = reload(sift)
# Read features
im1 = array(Image.open('D:\\Python\\chapter5\\crans_1_small.jpg'))
sift.process_image('D:\\Python\\chapter5\\crans_1_small.jpg', 'im1.sift')

im2 = array(Image.open('D:\\Python\\chapter5\\crans_2_small.jpg'))
sift.process_image('D:\\Python\\chapter5\\crans_2_small.jpg', 'im2.sift')

l1, d1 = sift.read_features_from_file('im1.sift')
l2, d2 = sift.read_features_from_file('im2.sift')

matches = sift.match_twosided(d1, d2)

ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)

d1n = d1[ndx]
d2n = d2[ndx2]
x1n = x1.copy()
x2n = x2.copy()

# In[7]:

figure(figsize=(16, 16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()

# def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
    """ Robust estimation of a fundamental matrix F from point
    correspondences using RANSAC (ransac.py from
    http://www.scipy.org/Cookbook/RANSAC).
    input: x1, x2 (3*n arrays) points in hom. coordinates. """

    from PCV.tools import ransac
    data = np.vstack((x1, x2))
    d = 10  # 20 is the original
    # compute F and return with inlier index
    F, ransac_data = ransac.ransac(data.T, model,
                                   8, maxiter, match_threshold, d, return_all=True)
    return F, ransac_data['inliers']

# find F through RANSAC
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-3)
print F

P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)

print P2
print F
# triangulate inliers and remove points not in front of both cameras
X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)

# plot the projection of X
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)
figure(figsize=(16, 16))
imj = sift.appendimages(im1, im2)
imj = vstack((imj, imj))

imshow(imj)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
    if (0 <= x1p[0][i] < cols1) and (0 <= x2p[0][i] < cols1) and (0 <= x1p[1][i] < rows1) and (0 <= x2p[1][i] < rows1):
        plot([x1p[0][i], x2p[0][i] + cols1], [x1p[1][i], x2p[1][i]], 'c')
axis('off')
show()

d1p = d1n[inliers]
d2p = d2n[inliers]

# Read features
im3 = array(Image.open('D:\\Python\\chapter5\\crans_2_small.jpg'))
sift.process_image('D:\\Python\\chapter5\\crans_2_small.jpg', 'im3.sift')
l3, d3 = sift.read_features_from_file('im3.sift')

matches13 = sift.match_twosided(d1p, d3)

ndx_13 = matches13.nonzero()[0]
x1_13 = homography.make_homog(x1p[:, ndx_13])
ndx2_13 = [int(matches13[i]) for i in ndx_13]
x3_13 = homography.make_homog(l3[ndx2_13, :2].T)

figure(figsize=(16, 16))
imj = sift.appendimages(im1, im3)
imj = vstack((imj, imj))

imshow(imj)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1_13[0])):
    if (0 <= x1_13[0][i] < cols1) and (0 <= x3_13[0][i] < cols1) and (0 <= x1_13[1][i] < rows1) and (
            0 <= x3_13[1][i] < rows1):
        plot([x1_13[0][i], x3_13[0][i] + cols1], [x1_13[1][i], x3_13[1][i]], 'c')
axis('off')
show()

P3 = sfm.compute_P(x3_13, X[:, ndx_13])

print P3
print P1
print P2
print P3

sift特征点匹配方法，匹配效果为：

基础矩阵F和第二个照相机矩阵P2的值如下：

[[ 3.54029526e-08 5.78566902e-06 -3.39212768e-03]
[-5.74552921e-06 -2.69837337e-07 2.28780647e-03]
[ 3.52101798e-03 -3.94749424e-03 1.00000000e+00]]
[[-2.09365738e+00 1.41205492e+00 6.17212907e+02 7.11074251e+02]
[ 2.41205469e+00 -1.62680602e+00 -7.11070730e+02 6.17208960e+02]
[ 4.09218924e-03 3.35431772e-03 -4.98016535e+00 1.00000000e+00]]
[[ 3.54029526e-08 5.78566902e-06 -3.39212768e-03]
[-5.74552921e-06 -2.69837337e-07 2.28780647e-03]
[ 3.52101798e-03 -3.94749424e-03 1.00000000e+00]]

[[ 2.14816980e-06 9.36923489e-07 -1.79658766e-03]
[-1.24402821e-06 2.77589004e-06 -2.62348680e-04]
[-8.68933562e-04 -1.07509791e-03 1.00000000e+00]]
[[-3.76869434e-01 -5.50354108e-02 2.09770131e+02 5.25978991e+02]
[ 9.44969513e-01 1.37988650e-01 -5.25979860e+02 2.09769056e+02]
[ 4.21825208e-05 1.72101847e-03 -3.83203539e-01 1.00000000e+00]]
[[ 2.14816980e-06 9.36923489e-07 -1.79658766e-03]
[-1.24402821e-06 2.77589004e-06 -2.62348680e-04]
[-8.68933562e-04 -1.07509791e-03 1.00000000e+00]]

三角剖分后，得到的第一张图和第二张图均含有最多场景点的匹配结果图如下：

三角剖分后，得到的第一张图和第三张图均含有最多场景点的匹配结果图如下：

第一个照相机矩阵p1，第二个照相机矩阵p2，第三照相机矩阵p3的值如下：

[[ 1.57220569e-03 -1.06043678e-03 -4.63391387e-01 -5.33978136e-01]
[-1.81145281e-03 1.22175358e-03 5.34078301e-01 -4.63490027e-01]
[-5.20585792e-06 -1.40315322e-06 4.61563909e-03 -7.46857189e-04]]
[[1 0 0 0]
[0 1 0 0]
[0 0 1 0]]
[[-2.09365738e+00 1.41205492e+00 6.17212907e+02 7.11074251e+02]
[ 2.41205469e+00 -1.62680602e+00 -7.11070730e+02 6.17208960e+02]
[ 4.09218924e-03 3.35431772e-03 -4.98016535e+00 1.00000000e+00]]
[[ 1.57220569e-03 -1.06043678e-03 -4.63391387e-01 -5.33978136e-01]
[-1.81145281e-03 1.22175358e-03 5.34078301e-01 -4.63490027e-01]
[-5.20585792e-06 -1.40315322e-06 4.61563909e-03 -7.46857189e-04]]

[[-4.70610432e-04 -6.87093872e-05 2.61950838e-01 6.56788856e-01]
[ 1.17997943e-03 1.72319540e-04 -6.56787833e-01 2.61938643e-01]
[ 2.37826828e-07 1.80543817e-07 -1.69962593e-04 1.02828112e-03]]
[[1 0 0 0]
[0 1 0 0]
[0 0 1 0]]
[[-3.76869434e-01 -5.50354108e-02 2.09770131e+02 5.25978991e+02]
[ 9.44969513e-01 1.37988650e-01 -5.25979860e+02 2.09769056e+02]
[ 4.21825208e-05 1.72101847e-03 -3.83203539e-01 1.00000000e+00]]
[[-4.70610432e-04 -6.87093872e-05 2.61950838e-01 6.56788856e-01]
[ 1.17997943e-03 1.72319540e-04 -6.56787833e-01 2.61938643e-01]
[ 2.37826828e-07 1.80543817e-07 -1.69962593e-04 1.02828112e-03]]

（三）三维重建

三维重建的四种主要方式：

1. 基于图像。应用广泛，精度比较低。
2. 使用探针或激光读书器逐点获取数据，进行整体三角化，此类方法测量精确，但速度很慢，难以短时间内获得大量数据。
3. 根据三维物体的断层扫面，得到二维图像轮廓，进行相邻轮廓的连接和三角化，得到物体表面形状。
4. 光学三维扫描仪。应用硬件光学三维扫描仪获得物体的点云数据，进行重建获得物体的整体表面信息。

基于图像的重建流程：

假设照相机已经标定，计算重建可以分为下面 4 个步骤：

1. 检测特征点，然后在两幅图像间匹配；
2. 由匹配计算基础矩阵；
3. 由基础矩阵计算照相机矩阵；
4. 三角剖分这些三维点。

编写代码：

# -*- coding: utf-8 -*-
from PIL import Image
from numpy import *
from pylab import *
import numpy as np
import camera
import homography
import sfm
import sift
# 标定矩阵
K = array([[2394,0,932],[0,2398,628],[0,0,1]])
# 载入图像，并计算特征


im1 = array(Image.open('D:\\Python\\chapter5\\alcatraz1.jpg'))
sift.process_image('D:\\Python\\chapter5\\alcatraz1.jpg', 'D:\\Python\\chapter5\\im1.sift')
l1, d1 = sift.read_features_from_file('D:\\Python\\chapter5\\im1.sift')

im2 = array(Image.open('D:\\Python\\chapter5\\alcatraz2.jpg'))
sift.process_image('D:\\Python\\chapter5\\alcatraz2.jpg', 'D:\\Python\\chapter5\\im2.sift')
l2, d2 = sift.read_features_from_file('D:\\Python\\chapter5\\im2.sift')

# 匹配特征
matches = sift.match_twosided(d1,d2)
ndx = matches.nonzero()[0]

# 使用齐次坐标表示，并使用 inv(K) 归一化
x1 = homography.make_homog(l1[ndx,:2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2,:2].T)
x1n = dot(inv(K),x1)
x2n = dot(inv(K),x2)

# 使用 RANSAC 方法估计 E
model = sfm.RansacModel()
E,inliers = sfm.F_from_ransac(x1n,x2n,model)
# 计算照相机矩阵（P2 是 4 个解的列表）
P1 = array([[1,0,0,0],[0,1,0,0],[0,0,1,0]])
P2 = sfm.compute_P_from_essential(E)

# 选取点在照相机前的解
ind = 0
maxres = 0
for i in range(4):
    # 三角剖分正确点，并计算每个照相机的深度
    X = sfm.triangulate(x1n[:,inliers],x2n[:,inliers],P1,P2[i])
    d1 = dot(P1,X)[2]
    d2 = dot(P2[i],X)[2]

    if sum(d1>0)+sum(d2>0) > maxres:
        maxres = sum(d1>0)+sum(d2>0)
        ind = i
        infront = (d1>0) & (d2>0)
    # 三角剖分正确点，并移除不在所有照相机前面的点
    X = sfm.triangulate(x1n[:,inliers],x2n[:,inliers],P1,P2[ind])
    X = X[:,infront]

    # 绘制三维图像
    from mpl_toolkits.mplot3d import axes3d
    fig = figure()
    ax = fig.gca(projection='3d')
    ax.plot(-X[0], X[1], X[2], 'k.')
    axis('off')
    # 绘制 X 的投影 import camera
    # 绘制三维点
    cam1 = camera.Camera(P1)
    cam2 = camera.Camera(P2[ind])
    x1p = cam1.project(X)
    x2p = cam2.project(X)

    # 反 K 归一化
    x1p = dot(K, x1p)
    x2p = dot(K, x2p)
    figure()
    imshow(im1)
    gray()
    plot(x1p[0], x1p[1], 'o')
    plot(x1[0], x1[1], 'r.')
    axis('off')
    figure()
    imshow(im2)
    gray()
    plot(x2p[0], x2p[1], 'o')
    plot(x2[0], x2[1], 'r.')
    axis('off')
    show()

代码运行效果如下：

a. ransac算法算出的模型参数

b. 带有特征点和二次投影重建的三维点的两幅图像

c.上图的三维重建

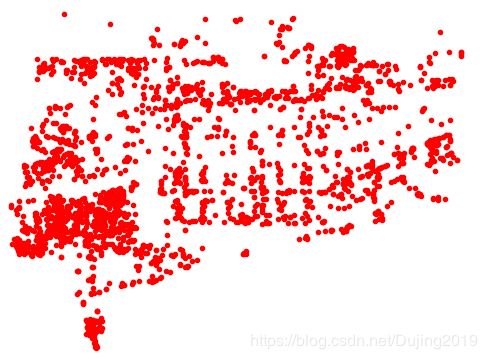
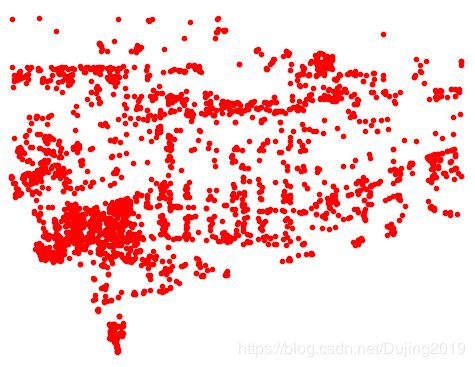
可以看到，二次投影后的点和原始特征位置不完全匹配， 但是相当接近。可以进一步调整照相机矩阵来提高重建和二次投影的性能。

编写代码遇到的问题，解决方案供参考：

错误1.
NameError: name ‘figure’ is not defined

解决：

from pylab import *

错误2：
TypeError: genfromtxt() got an unexpected keyword argument ‘missing’

解决：
将

corr = genfromtxt(‘D:\Python\chapter5\nview-corners’,dtype=‘int’,missing=’*’)

改写成

corr = genfromtxt(‘D:\Python\chapter5\nview-corners’)

错误3：
NameError: name ‘points3D’ is not defined

解决：

execfile(‘aaaaa.py’)

错误4：
x1 = points2D[0][:,corr[ndx,0]]
IndexError: arrays used as indices must be of integer (or boolean) type

解决：
将

corr = genfromtxt(‘D:\Python\chapter5\nview-corners’,dtype=‘int’,missing=’*’)

改写成

corr = genfromtxt(‘D:\Python\chapter5\nview-corners’,dtype=‘int’)