算法练习 - 五笔编码

题目描述

五笔的编码范围是a ~ y的25个字母，从1位到4位的编码，如果我们把五笔的编码按字典序排序，形成一个数组如下：
a, aa, aaa, aaaa, aaab, aaac, … …, b, ba, baa, baaa, baab, baac … …, yyyw, yyyx, yyyy， 其中a的Index为0，aa的Index为1，aaa的Index为2，以此类推。
 * 编写一个函数，输入是任意一个编码，比如baca，输出这个编码对应的Index；
 * 编写一个函数，输入是任意一个Index，比如12345，输出这个Index对应的编码。

题目分析

如果你之前做过另一个题目，“求字符的所有组合，当输入的字符串中含有相同的字符串时，相同的字符交换位置是不同的排列，但是同一个组合。举个例子，如果输入abc，它的组合有a、b、c、ab、ac、bc、abc。” 那么这个题目一出来起码不会觉得特别无从下手，其实就算没做过也不会特别无从下手，因为就是穷举利器嘛（即使写成漂亮的递归，仍然不能摆脱穷举的命运）。

这里自然不是为了分析这个递归穷举法（也许之后我会再单独写一篇阐述一下下）。所以技巧还是需要一些的。将题目要求的字符串排列组合起来，如下图示

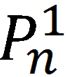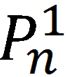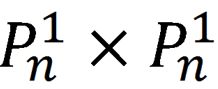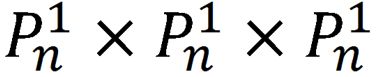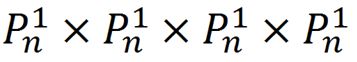根据排列组合的原理，单独来看每一位字符其可能的组合都是，把4位结合起来看，从第1位到第4位，其可能的排列组合分别是，，和。对于每个字符串的index需要拆分开一位一位看。

先来看最末位，即字符串有4位，前3为相同，只有最后一位不同，那么index = index‘+（*p-*p’）。举个例子

p' 是指向字符串aaaa的最后一位a的指针，p是指向字符串aaab的最后一位b的指针，那么aaab的index就等于aaaa的index‘加上字符b与字符a的距离（即’b‘-’a'）

接下来看倒数第二位，即前2位和最后1位相同，只有倒数第2位不同，那么index = index' +（*p-*p’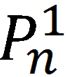）*( + 1)。举个例子

p' 是指向字符串aaaa的第3位a的指针，p是指向字符串aaba的指针，那么按排列规则，aaaa与aaba之间应该有字符串aaab,aaac,aaad...aaay, aab，再加上aaaa自身，这一系列字符串正好是一个完整的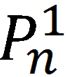。再来看一个例子，aaaa与aaca，它们之间应该有字符串aaab,aaac,aaad...aaay,aab, aaba,aabb,aabc...aaby, aac，正好是2倍的 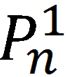+ 1。因此我们可以很容易得出结论，ndex = index' +（*p-*p’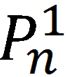）* ( + 1)

再看第2位，即第1位和最后2位相同，只有第2位不同，那么。举个例子

p' 是指向字符串aaaa的第3位a的指针，p是指向字符串abaa的指针，那么按排列规则，aaaa与abaa之间应该有字符串aaab,aaac,...aaay, aaba...aaby...aaya...aayy，再加上aaaa自身，这一系列字符串正好是一个完整的 + 。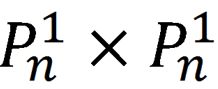

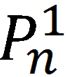最后就是首位了，即第1位不同，后面的3位相同，那么。举个例子

p' 是指向字符串 aaaa的第3位a的指针，p是指向字符串 baaa的指针，那么按排列规则，aaaa与baaa之间应该有字符串aaab,aaac,...aaay, aab,aaba...aaby...ab,aba,abaa,...abyy, ay,aya,ayaa...ayyy,b,ba,baa，再加上aaaa自身，这一系列字符串正好是一个完整的 + + 。

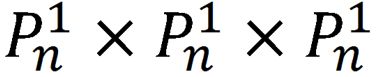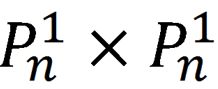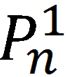综上，mnoq相对于字符串a的index应该是

分析完毕。输入index反向查找字符串正好是将上面的分析过程反过来，这里不详细记述。代码如下

/*
 * 五笔编码
 * 
 * 五笔的编码范围是a ~ y的25个字母，从1位到4位的编码，如果我们把五笔的编码按字典序排序，形成一个数组如下： 
 * a, aa, aaa, aaaa, aaab, aaac, … …, b, ba, baa, baaa, baab, baac … …, yyyw, yyyx, yyyy 
 * 其中a的Index为0，aa的Index为1，aaa的Index为2，以此类推。
 * 编写一个函数，输入是任意一个编码，比如baca，输出这个编码对应的Index；
 * 编写一个函数，输入是任意一个Index，比如12345，输出这个Index对应的编码。
 */
void WubiIndex(const string &input)
{
	const int NUM = 25;
	const char* p = input.c_str();
	int index = 0;
	int N = 3;
	
	int SUM[4] = {1};
	for(int i = 1; i < 4; ++i)
		SUM[i] = NUM * (SUM[i-1]) + 1;

	while(*p)
	{
		int temp = 0;
	    index += (*p -'a')*SUM[N--];
		++p;
	}
	cout<<"index is "< 0)
	{
		ch[M++] = 'a' + (index - 1)/SUM[N];
		index = (index - 1)%SUM[N--];
	}	
	cout<<"string is "<