HashTable详解

1、什么是哈希表？

哈希表（HashTable）又叫做散列表，是根据关键码值（即键值对）而直接访问的数据结构。也就是说，它通过把关键码映射到表中一个位置来访问记录，以加快查找速度。看到这里你可能比较疑惑，它是怎么加快查找速度的？下一节就有说明！这个映射函数就叫做散列（哈希）函数，存放记录的数组叫做散列表。

2、为什么哈希表的速度快？

在数据结构中，我们对两种数据结构应该会非常熟悉：数组与链表。数组的特点就是查找容易，插入删除困难；而链表的特点就是查找困难，但是插入删除容易。既然两者各有优缺点，那么我们就将两者的有点结合起来，让它查找容易，插入删除也会快起来。哈希表就是讲两者结合起来的产物。

3、哈希如何查找？

哈希的查找就是下面两个步骤：

<1>使用哈希函数将被查找的键转化为数组的索引。在理想的状态下，不同的键会被转化成不同的索引值。但是那是理想状态，我们实践当中是不可能一直是理想状态的。当不同的键生成了相同的索引的时候，也就是我们所说的冲突，我们这个时候就要处理冲突。

<2> 处理冲突的方法很多，后面我们介绍拉链法和线性探索法。

哈希表是一个时间和空间上平衡的例子。如果没有空间的限制，我们可以直接用键来作为数组的索引，这样可以将查找时间做到最快（O(1)）。如果没有时间的限制，我们可以使用无序链表进行顺序查找，这样只需要很少的内存。

4、什么是哈希函数？

哈希函数其实就是我们常说的哈希算法，主要应用在以下这几个方面：文件校验、数字签名、鉴权协议。常用的哈希算法有以下这些。

<1>MD5：MD5即Message-Digest Algorithm 5(信息-摘要算法5)，用于确保信息传输完整一致。MD5是输入不定长度信息，输出固定长度128bits的算法。

<2>SHA-1：常用于HTTPS传输和软件签名。

<3>SHA-2:SHA-224/SHA-256/SHA-384/SHA-512并成为SHA-2

<4>SHA-3:之前名为Keccak算法，是一个加密杂凑算法。

5、如何避免哈希冲突？

通过哈希函数，我们可以将键转化为数组的索引（0~M-1），但是对于两个或者多个键具有相同的索引值得情况，我们需要一种处理这种情况的方法。

<1>拉链法

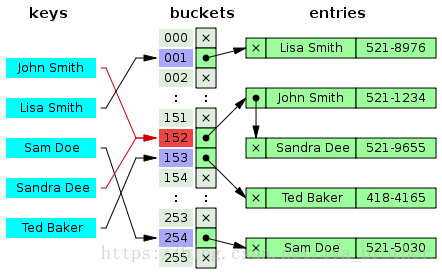
如下图所示，将大小为M的数组的每一个元素只想一个链表，链表中的每一个节点都存储散列值为该索引的键值对，这个就是拉链法。

图中，”John Smith”和”Sandra Dee”通过哈希函数指向152这个索引，该索引又指向了一个链表，在链表中依次存储了这两个字符串。

该方法的基本思想就是选择足够大的M，使得所有的链表都尽可能的短小，以保证查找的效率。对采用拉链法的哈希表实现的查找分为两步，首先是根据散列值找到对应的链表，然后沿着链表的顺序找到相应的键。

<2>线性探索法

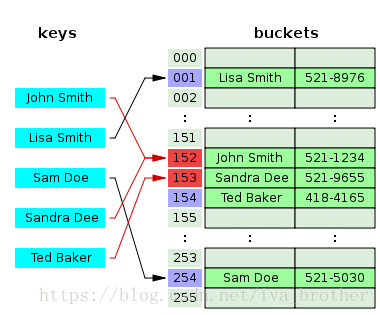
线性探测法是开放寻址法解决哈希冲突的一种方法，基本原理为，使用大小为M的数组来保存N个键值对，其中M>N，我们需要使用数组中的空位来解决碰撞冲突。如下图所示。

对照前面的拉链法，在该图中，”Ted Baker”有唯一哈希值153的，但是由于153被”Sandra Dee”占用了。而原先”Sandra Dee”和”John Smith”的哈希值都是152的，但是在对”Sandra Dee”进行哈希的是偶发现152已经被占用了，所以往下找发现153没有被占用，就将其存放在153。后面”Ted Baker”哈希到153上，发现被占用了，就会往下找，发现154没有被占用，所以将其存放到154上面。

开放寻址法中最简单的是线性探测法：当碰撞发生时即一个键的散列值被另外一个键占用时，直接检查散列表中下一个位置，即将索引值加1，这样的线性探测有三种结果：

<1>命中，该位置的键个被查找的键相同；

<2>未命中，键为空；

<3>继续查找，该位置的键和被查找的键不同。

那个这两种方法的性能上面有什么区别？对于拉链法，查找的效率在于链表的长度，一般我们应该保证长度的M/8~M/2之间，如果链表的长度大于M/2，我们可以扩充链表长度。如果长度在0~M/8时，我们可以缩短链表。对于线性探索法，动态调整数组的大小需要对所有的值重新进行散列并插入新的表中。

不管是拉链法还是散列法，这种动态调整链表或者数组的大小以提高查询效率的同时，还应该考虑动态改变链表或者数组大小的成本。散列表长度加倍的插入需要进行大量的探索，这种均摊成本很多时候需要考虑。

6、哈希碰撞攻击

我们知道如果哈希函数选择不当会使大量的键都会映射到相同的索引上，不管是采用拉链法还是开放寻址法解决冲突，在后面查找的时候都需要进行多次探测或者查找，在很多时候会使得哈希表的查找效率退化，而不再是常数时间。如下图描述的那样。

哈希攻击就是通过精心构造哈希函数，使得所有的键进过函数函数后都会映射到同一个或者几个索引上，将哈希表退化为一个单链表，这样哈希表的各种操作，比如插入、查找都会从O(1)退化到了链表的查找操作，这样会消耗大量的CPU资源，导致系统无法响应，从而达到拒绝服务供给（Denial of Service,DOS）的目的。

参考文章

https://blog.csdn.net/duan19920101/article/details/51579136

www.cnblogs.com/yangecnu/p/Introduce-Hashtable.html