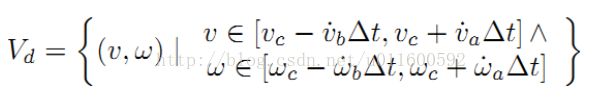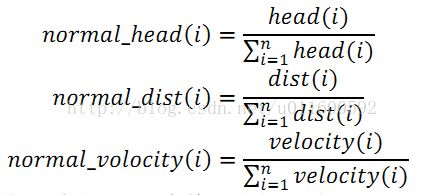机器人局部避障的动态窗口法(dynamic window approach)
概述:
机器人局部路劲规划方法有很多,ROS中主要采用的是动态窗口法(但是原论文中的dwa方法不一样,具体见后面)。动态窗口法主要是在速度(v,w)空间中采样多组速度,并模拟机器人在这些速度下一定时间(sim_period)内的轨迹。在得到多组轨迹后,对于这些轨迹进行评价,选取最优轨迹所对应的速度来驱动机器人运动。该算法突出点在与动态窗口这个名词,它的含义是依据移动机器人的加减速性能限定速度采样空间在一个可行的动态范围内。
1 机器人的运动模型
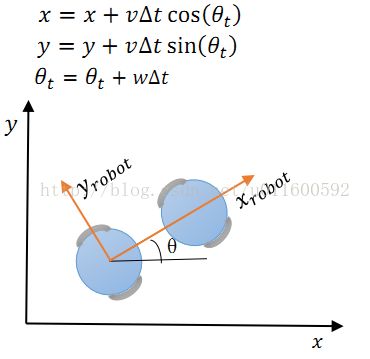
在动态窗口算法中,要迷你机器人的轨迹,需要知道机器人的轨迹,需要知道机器人的运动模型。它采用的是假设两轮移动机器人的轨迹是一段一段的圆弧或者直线(旋转速度为0时),一对(vt,wt)就代表一个圆弧轨迹。具体推导如下:
1.1 模型1:简单,程序中最常见,但不是动态窗口论文中的模型。
首先假设机器人不是全向移动的,即不能纵向移动,只能前进和旋转(vt,wt)。计算机器人轨迹时,先考虑两个相邻时刻,如下图所示。为简单起见,由于机器人相邻时刻(一般码盘采样周期ms计)内,运动距离短,因此可以将两相邻点之间的运动轨迹看成直线,即沿机器人坐标系x轴移动了![]() 。只需将该段距离分别投影在世界坐标系x轴和y轴上就能得到t+1时刻相对于t时刻机器人在世界坐标系中坐标移动的位移
。只需将该段距离分别投影在世界坐标系x轴和y轴上就能得到t+1时刻相对于t时刻机器人在世界坐标系中坐标移动的位移![]()
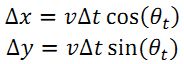
以此类推,如果你想推算一段时间内的轨迹,只需要将这段时间的位移增量累计求和就行了:
如果机器人是全向运动的,有y轴速度,那轨迹如何推算呢?
机器人坐标系的y轴有了速度,依葫芦画瓢,只需将机器人在机器人坐标y轴移动的距离投影到世界坐标系即可:
此时的轨迹推演只需将y轴移动的距离叠加在之前的计算公式上即可:
在ROS的轨迹推演中就使用的该公式,base_local_planner的轨迹采样程序也是使用的该公式(line 256 in simple_trajectory_generator.cpp):
1.2 模型2:
上面的计算中,假设相邻时间段内机器人的轨迹是直线,这是不准确的,更准确的做法是用圆弧来代替。正如dynamic window approach论文原文推到的那样,也如该博客下推导的那样(博客推导不严谨):
在这里,依然假设不是全向运动机器人,它做圆弧运动的半径为:
当旋转速度w不等于0时,机器人坐标为:
1.3 还有一些其他的推导方法,如文献[5、6]中得到的公式如下:
上面3个模型中,在程序中见得最多的就是模型1.
2 速度采样
机器人的轨迹运动模型有了,根据速度就可以推算出轨迹。因此只需采样很多速度,推算轨迹,然后评价这些轨迹好不好就行了。
速度如何采样是dynamic window approach的第二个核心:在速度(v,w)的二维空间中,存在无穷多组速度。但是根据机器人本身的限制和环境限制可以将采样速度控制在一定范围内:
2.1 移动机器人受自身最大速度最小速度的限制:
2.2 移动机器人受到电机性能的影响:
由于电机力矩有限,存在最大的加减速限制,因此移动机器人轨迹前向模拟的周期sim_period内,存在一个动态窗口,在该窗口内的速度是机器人能够实际达到的速度:
其中vc,wc是机器人的当前速度,其他标志对应最大加速度和最大减速度。
2.3 基于移动机器人安全的考虑:
为了能够在碰到障碍物前停下来,因此在最大减速度条件下,速度有一个范围:
其中dist(v,w)为速度(v,w)对应轨迹上离障碍物最近的距离,如下图弧线所示:
注意:这个条件并不是在采样一开始就能得到的。需要我们模拟出来机器人轨迹以后,找到障碍物位置,计算出机器人到障碍物之间的距离,然后看当前采样的这对速度能否在碰到障碍物之前停下来,如果能够停下来,那这对速度就是可接受的admissible。如果不能停下来,这对速度就得抛弃掉。
为了更直观的感受速度如何采样以及如何排除会碰到障碍的速度,将速度采样的伪代码列出如下:
-
首先在V_m∩V_d的范围内采样速度: -
allowable_v = generateWindow(robotV, robotModel) -
allowable_w = generateWindow(robotW, robotModel) -
然后根据能否及时刹车剔除不安全的速度: -
for each v in allowable_v -
for each w in allowable_w -
dist = find_dist(v,w,laserscan,robotModel) -
breakDist = calculateBreakingDistance(v)//刹车距离 -
if (dist > breakDist) //如果能够及时刹车,该对速度可接收 -
如果这组速度可接受,接下来利用评价函数对其评价,找到最优的速度组
同时注意:为了简化每组速度对应轨迹的计算,该算法假设机器人在往前模拟轨迹的这段时间(sim_period)内速度不变,知道下一时刻采样给定新的速度命令。
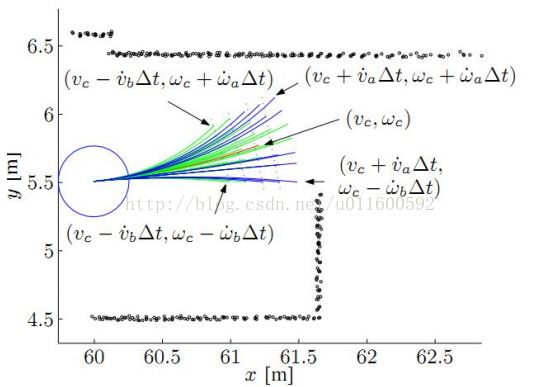
动态窗口采样的轨迹如下图所示:
3 评价函数
在采样的速度组中,有若干组轨迹是可行的,因此采用评价函数的方式为每条轨迹进行评价。在原始论文中,采用的评价函数如下:
3.1 方位角评价函数
heading(v,w)是用来评价机器人在当前设定的采样速度下,达到模拟轨迹末端时的朝向和目标之间的角度差距。如图所示:
原论文中是采用的的方式来评价,也就是越小,评价得分越高。
3.2 空隙
dist(v,w)代表机器人在当前轨迹上与最近的障碍物之间的距离。如果在这条轨迹上没有障碍物,那就将其设定一个常数。
3.3 速度
velocity(v,w)用来评价当前轨迹的速度大小。
3.4 平滑处理
也就是归一化,上面三个部分计算出来以后不是直接相加。而是每个部分在归一化以后,再相加。
如何归一化?
每一项除以每一项的总和:
其中,n为采样的所有轨迹,i为待评价的当前啊轨迹。
为什么要归一化?
归一化的目的是smoothing:例如障碍物距离,机器人传感器检测到的最小障碍物距离在二维空间中是不连续的,这条轨迹能够遇到障碍,旁边那边不一定能遇到。并且这条轨迹最小的障碍物距离是1m,旁边那条就是10m。那么障碍物距离的这种评价标准导致评价函数不连续,也会导致某个项在评价函数中太占优势,如这里的离障碍物距离10m相对于1m就太占优势。所以将它们归一化:
这样,都变成同一百分比了,每个障碍物最小距离是这100份中的一份。
总结起来三者构成的评价函数的物理意义是:在局部导航过程中,使得机器人避开障碍,朝着目标以较快速度行驶,缺一不可。
流程清楚以后:dwa算法的demo如下:
-
来源:http://adrianboeing.blogspot.com/2012/05/dynamic-window-algorithm-motion.html -
BEGIN DWA(robotPose,robotGoal,robotModel) -
laserscan = readScanner() -
allowable_v = generateWindow(robotV, robotModel) -
allowable_w = generateWindow(robotW, robotModel) -
for each v in allowable_v -
for each w in allowable_w -
dist = find_dist(v,w,laserscan,robotModel) -
breakDist = calculateBreakingDistance(v) -
if (dist > breakDist) //can stop in time -
heading = hDiff(robotPose,goalPose, v,w) -
//clearance与原论文稍不一样 -
clearance = (dist-breakDist)/(dmax - breakDist) -
cost = costFunction(heading,clearance, abs(desired_v - v)) -
if (cost > optimal) -
best_v = v -
best_w = w -
optimal = cost -
set robot trajectory to best_v, best_w -
END
引申到ROS:
在ROS的dwa应用中,好像只用了窗口采样速度,到障碍物的最小距离以及刹车距离都没计算,如果某条轨迹上有障碍,那直接丢弃这条轨迹。并且ROS中的评价函数也不是用的这个,采用的是Gerkey的论文《planning unstructured Terrain》种的评价函数。