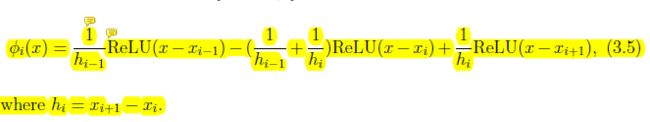神经网络和有限元方法

用神经网络来表示有限元函数

今天，我想分享的东西是许进超老师的一篇文章，ReLU Deep Neural Networks and Linear Finite Elements。你可以理解为，这是一篇译文。

主要内容

它主要是关于神经元数与层数，在用DNN表示线性有限元的时候。它告诉我们，当维数大等于2的时候，我们至少需要两个隐藏层，在用ReLu DNN表示线性有限元函数的时候。因为在其它的文献中，$\lceil {\text{log}}_2(d+1)\rceil$at most被介绍了，当用ReLu DNN表示分片线性函数的时候。所以，当d大等于2时，2层是必要且充分的，也就是说它是最优的（optimal）。

另一方面，文章也给了我们一个估计，关于神经元的数目that are need。

再一个，作者介绍了low bit-width的DNN模型，思想来自于用DNN去表示分片线性函数的特殊结构。

最后，作者以一维的两点边值问题，做了一个数值实验。

简介

近年来，为什么DNN模型能work得这么好，依然是不清楚的。为了弄清楚它，我们可以研究DNN所表示的函数类的逼近属性（approximation properties）和表达能力（expressive power）。

万有逼近定理（Universal Approximation Theory）告诉我们，任何单隐层神经网络能够逼近任何连续函数。万有逼近定理见如下文章：

M. Leshno, V.Y. Lin, A. Pinkus and S. Schocken, Multilayer feedforward networks with a nonpolynomial activation function can approximate any function,Neural networks, 6(1993), 861-867.

另外，我们可以看到下面一个陈述是正确的：

Every ReLU DNN function in $R^d$ represents a continuous piecewise linear (CPWL) function dened on a number of polyhedral subdomains.

近年来，上述statement相反（converse）的论述也被证明是正确的。

更近一步，关于神经网络去表示分片线性函数的一个层数的论述，被证明了，如下：

Every CPWL function in $R^d$ can be represented by a ReLU DNN model with at most $\lceil {\text{log}}_2(d+1)\rceil$ hidden layers.

有了这些考虑，作者想要知道的就是：

• How many numbers of neurons are needed?
• What is the minimal number of layers that are needed?

结论是，我们需要用$O(d{2}^{mm!})$数目的神经元去表示CPWL（continual piecewise linear），m表示子区域的数目。

进一步，为了得到更少数目的DNN表示，作者在文章中考虑了更特殊的一类函数，叫做LFE（Linear Finit Element）。

因为LFE是节点基函数（nodal basis funciotns）的一个线性组合，所以我们只需要研究节点基函数的DNN表示。

最后，作者证明了LFE能用$O(d{\kappa }^{d}N)$数目的神经元表示，用$O(d)$层的一个网络，这里的$\kappa$取决于网格的正则性。

另外一个问题，多少层呢？对于LFE而言，2 at least当维数大于2时，$\lceil {\text{log}}_2(d+1)\rceil$at most，那么，其实d=2,3时，$\lceil {\text{log}}_2(d+1)\rceil$层就是最优的。当d更大是，是否是最优的，仍然是一个开放的问题。

到底CPWL和LFE的区别是什么呢？剖分是否确定？不是，只不过是用两种不同的角度看问题，得到的不同的网络而已，它们的神经元个数和层数是不同的。

作者还介绍了heavily quantized weights去压缩神经网络，比如binary和ternary权重模型。

最后，一个数值例子表明，使用 ReLU DNN 的Galerkin方法比适应性有限元方法逼近结果要好。

一个普通标题	CPWL	LFE	LFE(regularity)
神经元数目	$O(d{2}^{mm!})$	$O(k_{h}N)$	$O(d{\kappa }^{d}N)$
层数	2 at least($d\ge 2$,LFE),${\text{log}}_2(d+1)$at most	$\lceil {\text{log}}_2{k}_h\rceil +1$	$O(d)$

ReLU DNN的基本性质

首先，我们需要介绍一些记号。

我们把$\Theta$定义为：

定义作用于向量的激活函数$\sigma$为:

那么，给定$d,c,k\in {\mathbb{N}}^{+}$，并且：

那么，一般的从${\mathbb{R}}^d$到${\mathbb{R}}^c$可以写为：

这里我们假定$f^0(x)=\Theta (x)$。更简单地，我们可以写为：

这里的${\Theta }^i$是表示第i层到第i+1层的。一般我们称这样的DNN为k+1层DNN，或者说有k个隐藏层。

ReLU（rectified linear unit）的定义如下：

容易看到ReLU函数是CPWL的，自然它们的线性组合也是CPWL的。那么，我们会有如下一个引理：

我们把J个隐藏层且输出为一个变量的ReLu DNN，用一个记号来表示，即：

首先，让我们来看一下$DN{N}_1$，也就是有一个隐藏层的ReLu DNN，也就是：

这里的上标m表示隐藏层神经元的数目。

restrict $DN{N}_1^m$在$\Omega$，我们用如下的记号：

一些文献已经证明了，$DN{N}_1(\Omega )$在$C^0(\Omega )$上是稠密的（dense）。

当然，关于ReLu DNN，我们还有一个渐近（asymptotic）误差估计：

这里的hat是表示傅里叶变换。

另外，我们还有一个定理：

LFE的ReLu DNN表示

我们知道，CPWL能被ReLu DNN表示出来。线性有限元函数（Linear Finite Element Function，LFE）是一类特殊的CPWL。它也能被ReLu DNN表示出来。

为了说明这一点，我们先回顾一下有限元方法的相关知识，以及引入我们的符号。

有限元网格$T_h=\{{\tau }_k\}$，节点表示为$N_h$，那么分片线性函数空间可以写为：

节点基函数（nodal basis function）为：

对任何$v\in V_h$，我们有：

用$N_i$表示与i节点有关的单元的标号，即：

我们用$k_h$表示和节点有关的单元数目的最大值（maximum），也就是：

第i个节点的支集表示为：

我们说$T_h$是局部凸（locally convex），如果每个支集是凸的。

---

下面我们来看看局部凸网格的LFE的ReLU DNN表示。

因为分片线性函数可以用节点基函数线性表出，所以我们我们只需要研究节点基函数的ReLU DNN表出。

一维情况下，我们有：

对于多维的情况，我们先介绍一个引理：

这里的$g_k$是节点基函数的不同“片”，在整个定义域上的一个延伸。把它们取个最小，就得到了节点基函数。这个证明有点繁琐（Tedious）。让我们skip it。

关于这个引理有个remark：

下面我们介绍一个重要的定理：

证明如下：

我们可以将取最小值写成单隐藏层ReLU NN，如下：

我可以check it，虽然我不知道是怎么想到它的。其实，这是一个单隐层的ReLU DNN。两个到四个，再到一个。

根据之前那个引理，我们有：

为了方便，我们把$N(i)$写为：

那么，我们有：

我们可以对split出来的两项继续做划分，直到最后为1项或者2项。然后，我们利用：

根据以上的过程，我们知道，我们可以将基函数写成$\lceil {\text{log}}_2{k}_h\rceil +1$个隐藏层的DNN。WHY + 1？每一次划分不应该加两层吗？

考虑二叉树的结构，k层的二叉树总共有$2^k-1$个节点，那么神经元的个数大概（至多）为：

根据CWPL和节点基函数的表出关系，我们能得到分片线性函数能用$\lceil {\text{log}}_2{k}_h\rceil +1$的隐藏层表出。神经元的数目最多为$O(k_{h}N)$。

我们现在考虑一类所谓的形状规则的有限元网格，满足：

那么，我们有如下推论：

---

DNN方法的一个误差估计，考虑$DN{N}_1$，有如下结论：

事实上，后面会提到，单隐层的DNN是没有办法表示线性有限元函数的。

我们可以找到一个DNN的结构，使得用其去逼近有限元函数的结果更好：

维数大于1时，单隐层ReLU DNN无法表示LFE

浅层的ReLU DNN是无法精确地表示某些有限元函数的，精确描述如下：

这个证明啊，really a trifle。作者用了三页纸来完成这个证明。我这里就不提了。

这也是这篇文章的一个主要结果之一。

一般CPWL的ReLU DNN逼近（approach）

一般的方法，相比于前面提到的逼近方法，需要更少的层数，但是需要多得多（significantly，extremely）的神经元。

下面先不带证明地列出一些主要的结果：

这里的$f_i$是分片线性函数在片${\Omega }_i$上的值。

我们也有lattice表示定理，如下：

进一步，我们有这样一个结果：

这个定理告诉我们，我们可以用不超过${\text{log}}_2\lceil d+1\rceil$的隐藏层去表示它。

这个结果和前面的LFE的表示结果相比起来，虽然需要的层数降低了一些，但是需要的神经元多了非常多。

至此，对于一个局部凸的有限元网格，我们现在又两种不同的方式来表示它。

我们用这种表示CPWL的一般方式来表示FEL，有如下的一个结果：

由此，我们就可以比较出两个网络结构来表示分片线性函数的一个差异，一个需要$\lceil {\text{log}}_2(d+1)\rceil$隐层$O(d{2}^{(d+1)k_h})$的神经元，一个需要$\lceil {\text{log}}_2{k}_h\rceil +1$隐层$O(k_{h}N)$的神经元。前者虽然层数少，但是需要多得多的神经元。

低位宽的DNN模型

这部分介绍了一种特殊的ReLU DNN模型，它能表示所有的CPWL函数。它的参数要么是0，要么是2的次方，也就是说：

By our results in previous sections, we find a special family of ReLU DNN which has at most one general layers and all other layers with low bit-width parameters.

不加证明，我们有如下结果：

数值算例

DNN方法求解PDE，考虑如下模型问题：

一般使用DNN求解PDE用的是配点方法，也就是一个最小二乘问题：

这里的$u_N$是DNN的输出，使用平滑的激活函数，比如说sigmoid函数。

当然，还有一些其他的方法。

有限元方法一般采用适应有限元方法和移动网格方法。

适应网格方法有如下的误差估计：

DNN方法一般不需要网格，但是也需要离散点。DNN-Galerkin方法连点都不需要。

单隐层DNN的误差估计如下所示：

这里$\hat{u}$是将函数延拓到整个（entire）区间上后做的傅里叶变换。

---

我们来做一个一维的两点边值问题的例子。考虑如下模型问题：

剖分网格如下：

定义单隐层ReLU DNN为：

这里的${\theta }_i$表示区间$[t_{i-1},t_i]$上的斜率。

为了满足边界条件，我们需要有约束（上标到N，文中写错了）：

我们最小化能量函数：

交替以下两个步骤：

结论

足够多层的ReLU DNN是可以重构有限元函数的，文中讨论了两种不同的逼近方式。

One theoretically interesting question addressed in this paper concerns the minimal number of layers that are needed in a DNN model to reproduce general continuous piecewise linear functions.

作者证明了维数大于1是，最小需要两个隐藏层来表示分片函数，由于上限${\text{log}}_2(d+1)$的约束，二三维的时候，${\text{log}}_2(d+1)$就是最优的，更高维的时候，是否是最优的，还不知道。

不说消耗的事情，一维例子表明DNN的Galerkin逼近是比适应有限元方法是更精确的。但是呢，computational cost is a serious issue。