ML算法推导细节08—极端梯度提升XGBoost
探究算法细节,深入了解算法原理
XGBoost的参考资料
- XGBoost: A Scalable Tree Boosting System,论文原文,KDD@2016,华盛顿大学,陈天奇博士
- XGBoost PPT资料,陈天奇
XGBoost
- 1. 回归树集成(Regression Tree Ensemble)
- 2. XGBoost(Gradient Boosting)
- 2.1 目标函数的近似表达式(二阶泰勒展开)
- 2.2 改进树的定义
- 2.3 定义树的复杂度
- 2.4 重写目标函数
- 2.5 最小化目标函数的解
- 2.6 寻找最佳的单棵树
- 2.6.1 使用贪心策略学习一颗树
- 3. XGBoost的总结
- 4. XGBoost论文原文解析
- 4.1 Introduction
- 4.2 Tree Boosting
- 4.3 Split Finding Algorithms
- 4.3.1 Basic Exact Greedy Algorithm
- 4.3.2 Approximate Algorithm
- 4.3.3 Weighted Quantile Sketch(加权分位数略图)
- 4.3.4 Sparsity-aware Split Finding
- 4.4 System Design
- 4.4.1 Column Block for Parallel Learning(并行化)
- 4.4.2 Cache-aware Access
- 4.4.3 Blocks for Out-of-core Computation
- 4.5 Related Works
- 4.6 End to End Evalutions
- 5. XGBoost 调参
- 5.1 XGBoost优点
- 5.2 XGBoost参数详解
- 5.2.1 通用参数
- 5.2.2 tree booster参数
- 5.2.3 学习目标参数
- 5.2.4 XGBoost基本方法和默认参数
- 6. XGBoost接口
- 6.1 XGBoost原生接口——分类问题
- 6.2 XGBoost的sklearn接口——分类问题
- 6.3 XGBoost 调参经验
1. 回归树集成(Regression Tree Ensemble)
【作者PPT内容】
(1)XGBoost全称:eXtreme Gradient Boosting 极端梯度提升
(2)学习算法的目标函数
O b j ( Θ ) = L ( Θ ) + Ω ( Θ ) Obj(\Theta)=L(\Theta)+\Omega(\Theta) Obj(Θ)=L(Θ)+Ω(Θ)
- L ( Θ ) L(\Theta) L(Θ) 训练损失,衡量训练集的拟合效果
- Ω ( Θ ) \Omega(\Theta) Ω(Θ) 正则化,衡量模型的复杂度
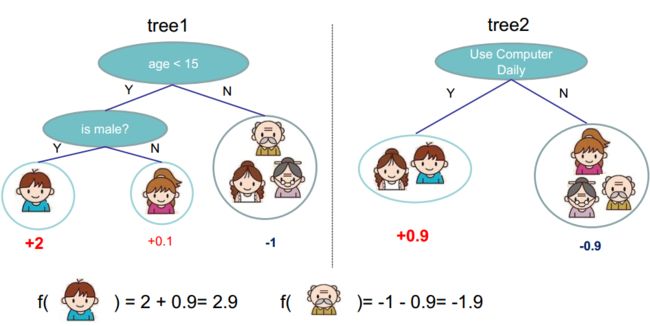
(3)集成CART回归树
例子:输入特征有年龄、性别、职业等,判断一个人是否喜欢电脑游戏。
- w 11 = 2 , w 12 = 0.1 , w 13 = − 1 , w 21 = 0.9 , w 22 = − 0.9 w_{11}=2,w_{12}=0.1,w_{13}=-1,w_{21}=0.9,w_{22}=-0.9 w11=2,w12=0.1,w13=−1,w21=0.9,w22=−0.9 是每个叶子节点的预测分数
- 预测结果是每棵树预测的分数之和
- 树的集成方法,可以学习到特征之间的高阶交互信息
假设有 K K K棵树,则预测分数为:
y i ^ = ∑ k = 1 K f k ( x i ) \hat{y_i}=\sum_{k=1}^{K}f_k(x_i) yi^=k=1∑Kfk(xi)
目标函数为:
O b j = ∑ i = 1 n l ( y i , y i ^ ) + ∑ k = 1 K Ω ( f k ) Obj=\sum_{i=1}^{n}l(y_i,\hat{y_i})+\sum_{k=1}^{K}\Omega(f_k) Obj=i=1∑nl(yi,yi^)+k=1∑KΩ(fk)
- 信息增益对应训练损失
- 剪枝对应正则化
- 最大深度限制树模型
- 平滑叶子节点的值对应叶子节点值的L2正则化
2. XGBoost(Gradient Boosting)
【作者PPT内容】
(1)第 t t t 轮的模型表达式为:
y i ^ ( t ) = ∑ k = 1 t f k ( x i ) = y i ^ ( t − 1 ) + f t ( x i ) \hat{y_i}^{(t)}=\sum_{k=1}^{t}f_k(x_i)=\hat{y_i}^{(t-1)}+f_t(x_i) yi^(t)=k=1∑tfk(xi)=yi^(t−1)+ft(xi)
其中 f t ( x ) f_t(x) ft(x) 是需要在第 t t t 轮学习的。找出 f t ( x ) f_t(x) ft(x) 最小化以下目标函数:
O b j ( t ) = ∑ i = 1 n l ( y i , y i ^ ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t Obj^{(t)}=\sum_{i=1}^{n}l\left(y_i,\hat{y_i}^{(t-1)}+f_t(x_i)\right)+\Omega(f_t)+constant Obj(t)=i=1∑nl(yi,yi^(t−1)+ft(xi))+Ω(ft)+constant
(2)如果是平方损失,去掉常数项,则目标函数变为:
O b j ( t ) = ∑ i = 1 n [ y i − ( y i ^ ( t − 1 ) + f t ( x i ) ) ] 2 + Ω ( f t ) + c o n s t a n t = ∑ i = 1 n [ 2 ( y i ^ ( t − 1 ) − y i ) f t ( x i ) + f t ( x i ) 2 ] + Ω ( f t ) \begin{aligned} Obj^{(t)} &= \sum_{i=1}^{n}\left[y_i-(\hat{y_i}^{(t-1)}+f_t(x_i))\right]^2+\Omega(f_t)+constant \\&= \sum_{i=1}^{n}\left[2(\hat{y_i}^{(t-1)}-y_i)f_t(x_i)+f_t(x_i)^2\right]+\Omega(f_t) \end{aligned} Obj(t)=i=1∑n[yi−(yi^(t−1)+ft(xi))]2+Ω(ft)+constant=i=1∑n[2(yi^(t−1)−yi)ft(xi)+ft(xi)2]+Ω(ft)
- 其中 y i ^ ( t − 1 ) − y i \hat{y_i}^{(t-1)}-y_i yi^(t−1)−yi 被称为前一轮的残差
2.1 目标函数的近似表达式(二阶泰勒展开)
(1)二阶泰勒展开公式为:
f ( x + Δ x ) ≃ f ( x ) + f ′ ( x ) Δ x + 1 2 f ′ ′ ( x ) Δ x f(x+\Delta x)\simeq f(x)+f^{'}(x)\Delta x+\frac{1}{2}f^{''}(x)\Delta x f(x+Δx)≃f(x)+f′(x)Δx+21f′′(x)Δx
(2)如果不是平方损失,目标函数很复杂
O b j ( t ) = ∑ i = 1 n l ( y i , y i ^ ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t Obj^{(t)}=\sum_{i=1}^{n}l\left(y_i,\hat{y_i}^{(t-1)}+f_t(x_i)\right)+\Omega(f_t)+constant Obj(t)=i=1∑nl(yi,yi^(t−1)+ft(xi))+Ω(ft)+constant
(3)定义损失函数对第 t − 1 t-1 t−1 轮的强学习器 y i ^ ( t − 1 ) \hat{y_i}^{(t-1)} yi^(t−1) 的一阶偏导和二阶偏导
g i = ∂ y i ^ ( t − 1 ) l ( y i , y i ^ ( t − 1 ) ) g_i=\partial_{\hat{y_i}^{(t-1)}}l(y_i,\hat{y_i}^{(t-1)}) gi=∂yi^(t−1)l(yi,yi^(t−1))
h i = ∂ y i ^ ( t − 1 ) 2 l ( y i , y i ^ ( t − 1 ) ) h_i=\partial^2_{\hat{y_i}^{(t-1)}}l(y_i,\hat{y_i}^{(t-1)}) hi=∂yi^(t−1)2l(yi,yi^(t−1))
(4)目标函数的近似表达式为:
O b j ( t ) = ∑ i = 1 n [ l ( y i , y i ^ ( t − 1 ) ) + g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) + c o n s t a n t Obj^{(t)}=\sum_{i=1}^{n}\left[l(y_i,\hat{y_i}^{(t-1)})+g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)\right]+\Omega(f_t)+constant Obj(t)=i=1∑n[l(yi,yi^(t−1))+gift(xi)+21hift2(xi)]+Ω(ft)+constant
(5)去掉常数项,目标函数变为:
O b j ( t ) = ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) Obj^{(t)}=\sum_{i=1}^{n}\left[g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)\right]+\Omega(f_t) Obj(t)=i=1∑n[gift(xi)+21hift2(xi)]+Ω(ft)
- f t ( x ) f_t(x) ft(x) 的学习仅仅取决于 g i , h i g_i, h_i gi,hi
2.2 改进树的定义
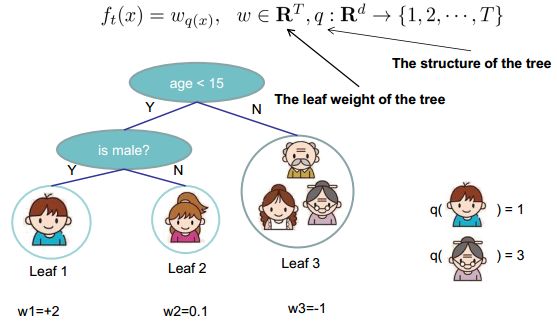
通过叶子节点中的分数向量和叶子索引映射函数来定义树,该函数将一个实例映射到一个叶子节点。
f t ( x ) = w q ( x ) , w ∈ R T , q : R d → { 1 , 2 , . . . , T } f_t(x)=w_{q(x)}, \quad w \in R^T, \quad q:R^d \rightarrow \{1,2,...,T\} ft(x)=wq(x),w∈RT,q:Rd→{1,2,...,T}
- 其中 w i w_i wi 是叶子节点的权重,即叶子节点的分数。
- q q q 是树的结构
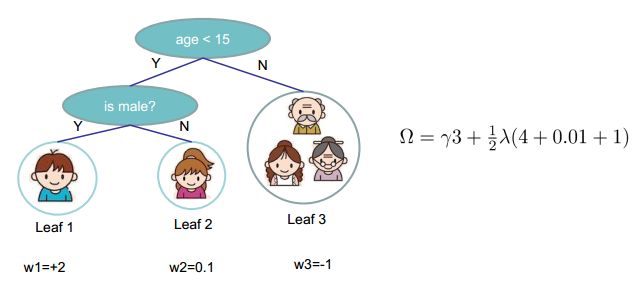
2.3 定义树的复杂度
利用叶子节点数 T T T,和叶子节点分数的L2范数 w j 2 w_j^2 wj2 共同定义模型的复杂度
Ω ( f t ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \Omega(f_t)=\gamma T+\frac{1}{2}\lambda\sum_{j=1}^{T}w_j^2 Ω(ft)=γT+21λj=1∑Twj2
2.4 重写目标函数
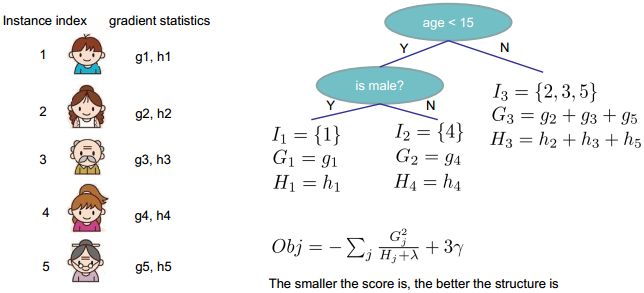
将叶子节点 j j j 中的实例样本定义为:
I j = { i ∣ q ( x i ) = j } I_j=\{i|q(x_i)=j\} Ij={i∣q(xi)=j}
根据叶子节点将目标函数重写为:
O b j ( t ) ≃ ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) = ∑ i = 1 n [ g i w q ( x i ) + 1 2 h i w q 2 ( x i ) ] + γ T + 1 2 λ ∑ j = 1 T w j 2 = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T \begin{aligned} Obj^{(t)} & \simeq \sum_{i=1}^{n}\left[g_if_t(x_i)+\frac{1}{2}h_if_t^2(x_i)\right]+\Omega(f_t) \\ & = \sum_{i=1}^{n}\left[g_iw_q(x_i)+\frac{1}{2}h_iw_q^2(x_i)\right]+\gamma T+\frac{1}{2}\lambda\sum_{j=1}^{T}w_j^2 \\ &=\sum_{j=1}^{T}\left[(\sum_{i \in I_j}g_i)w_j+\frac{1}{2}(\sum_{i \in I_j}h_i+\lambda)w_j^2\right]+\gamma T \end{aligned} Obj(t)≃i=1∑n[gift(xi)+21hift2(xi)]+Ω(ft)=i=1∑n[giwq(xi)+21hiwq2(xi)]+γT+21λj=1∑Twj2=j=1∑T⎣⎡(i∈Ij∑gi)wj+21(i∈Ij∑hi+λ)wj2⎦⎤+γT
2.5 最小化目标函数的解
(1)对于单变量的平方函数,有如下结论:
arg min x G x + 1 2 H x 2 = − G H , H > 0 \arg \min_{x} Gx+\frac{1}{2}Hx^2=-\frac{G}{H}, \quad H>0 argxminGx+21Hx2=−HG,H>0
min x G x + 1 2 H x 2 = − 1 2 G 2 H \min_{x} Gx+\frac{1}{2}Hx^2=-\frac{1}{2}\frac{G^2}{H} xminGx+21Hx2=−21HG2
(2)替换目标函数中的系数
定义如下系数:
G j = ∑ i ∈ I j g i G_j=\sum_{i \in I_j}g_i Gj=i∈Ij∑gi
H j = ∑ i ∈ I j h i H_j=\sum_{i \in I_j}h_i Hj=i∈Ij∑hi
目标函数变为:
O b j ( t ) ≃ ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T = ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T \begin{aligned} Obj^{(t)} & \simeq \sum_{j=1}^{T}\left[(\sum_{i \in I_j}g_i)w_j+\frac{1}{2}(\sum_{i \in I_j}h_i+\lambda)w_j^2\right]+\gamma T \\ & = \sum_{j=1}^{T}\left[G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2\right]+\gamma T \end{aligned} Obj(t)≃j=1∑T⎣⎡(i∈Ij∑gi)wj+21(i∈Ij∑hi+λ)wj2⎦⎤+γT=j=1∑T[Gjwj+21(Hj+λ)wj2]+γT
(3)假设树的结构 q ( x ) q(x) q(x) 是固定的,求得叶子节点的最佳权重、最小目标值(结构得分)为:
w j ∗ = − G j H j + λ w_j^*=-\frac{G_j}{H_j+\lambda} wj∗=−Hj+λGj
O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj=-\frac{1}{2}\sum_{j=1}^{T}\frac{G_j^2}{H_j+\lambda}+\gamma T Obj=−21j=1∑THj+λGj2+γT
(4)最小目标值计算:
- Obj衡量了树结构的好坏
2.6 寻找最佳的单棵树
- 枚举所有可能的树结构 q q q
- 计算结构得分, O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj=-\frac{1}{2}\sum_{j=1}^{T}\frac{G_j^2}{H_j+\lambda}+\gamma T Obj=−21∑j=1THj+λGj2+γT
- 找出最好的树结构,即Obj最小的树,使用最佳叶子节点权重 w j ∗ = − G j H j + λ w_j^*=-\frac{G_j}{H_j+\lambda} wj∗=−Hj+λGj
2.6.1 使用贪心策略学习一颗树
(1)从深度为0的树开始。
(2)对树的每个叶子节点,试图去分裂。增加分裂后的目标变化是:
- 这个公式形式上跟ID3算法(采用entropy计算增益) 、CART算法(采用gini指数计算增益) 是一致的,都是用分裂后的某种值减去分裂前的某种值,从而得到增益
(3)寻找最佳分裂
从左到右线性扫描经过排序的实例,找出特征的最佳分割。
- 对每个特征,按照特征值,排序实例(样本)
- 使用线性扫描,寻找最佳分割特征
- 停止分裂,如果最佳分裂有一个负增益
- 生成一个最大深度的决策树,递归的剪枝负增益的分裂节点
3. XGBoost的总结
(1)xgboost与传统的GBDT相比,对代价函数进行了二阶泰勒展开,同时用到了一阶与二阶导数,而GBDT在优化时只用到了一阶导数的信息,个人认为类似牛顿法与梯度下降的区别。
(2)xgboost在损失函数里加入的正则项可用于控制模型的复杂度。
- 正则项里包含了树的叶子节点个数、每个叶子节点上输出score的L2模的平方和。
- 从Bias-variance trade-off角度来讲,正则项降低了模型的variance,使学习出来的模型更加简单,防止过拟合,这也是xgboost优于传统GBDT的一个特性。
(3)传统GBDT以CART回归树作为基分类器,xgboost还支持线性分类器,这个时候xgboost相当于带L1和L2正则化项的逻辑回归(分类问题)或线性回归(回归问题)。
(4)Shrinkage(缩减),相当于学习速率(xgboost中的eta)。
- xgboost在进行完一次迭代后,会将叶子节点的权重乘上该系数,主要是为了削弱每棵树的影响,让后面有更大的学习空间。
- 实际应用中,一般把eta设置得小一点,然后迭代次数设置得大一点。
- 传统GBDT的实现也有学习速率
(5)列抽样(column subsampling)。xgboost借鉴了随机森林的做法,支持列抽样,不仅能降低过拟合,还能减少计算,这也是xgboost异于传统GBDT的一个特性。
(6)对缺失值的处理。对于特征的值有缺失的样本,xgboost可以自动学习出它的分裂方向。
(7)xgboost工具支持并行。boosting不是一种串行的结构吗?怎么并行的?
- 注意xgboost的并行不是tree粒度的并行,xgboost也是一次迭代完才能进行下一次迭代的(第t次迭代的代价函数里包含了前面t-1次迭代的预测值)。
- xgboost的并行是在特征粒度上的。我们知道,决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),xgboost在训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代中重复地使用这个结构,大大减小计算量。
- 这个block结构也使得并行成为了可能,在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。
(8)可并行的近似直方图算法。
- 树节点在进行分裂时,我们需要计算每个特征的每个分割点对应的增益,即用贪心法枚举所有可能的分割点。
- 当数据无法一次载入内存或者在分布式情况下,贪心算法效率就会变得很低,所以xgboost还提出了一种可并行的近似直方图算法,用于高效地生成候选的分割点。
4. XGBoost论文原文解析
以上3节内容是PPT中的资料,本节主要看一下【论文原文】的一些细节部分。
【XGBoost: A Scalable Tree Boosting System】
- 从题目中就可以看出来,这篇文章重点讲的是一个system,而不是algorithm
- 本文的重点大篇幅地介绍了xgb整个系统是如何搭建,如何实现的,在模型算法的公式改进上只做了一点微小的工作。
- 摘要:XGBoost可用比现有系统少得多的资源来处理数十亿规模的数据。
4.1 Introduction
主要创新点:
-
构建高度可扩展的端到端的提升树系统。 XGBoost成功的最重要因素是其在所有情况下的可扩展性
-
该系统在单台机器上的运行速度比现有流行解决方案快十倍以上,并可在分布式或内存有限的环境中扩展到数十亿的数据规模。
-
提出一个理论上合理的加权分位数略图。(分裂节点时可以不用遍历所有点,省时间)
-
引入新颖的稀疏感知算法用于并行树学习。(令缺失值有默认方向)
-
提出有效的用于核外树形学习的缓存感知块结构。(用缓存加速寻找排序后被打乱的索引的列数据)
4.2 Tree Boosting
- 基本思想与GBDT一样,都是按照损失函数的负梯度方向提升
- 损失函数进行了泰勒二次展开(不理解为什么用二阶导数),求近似解
- 正则化项除了叶子节点数之外,加入了叶子节点得分的L2范数
- shrinkage相当于学习速率
- column(feature) subsampling,与RF类似。使用者反馈列的子采样比行的子采样更能防止过拟合,列的子采样也加速了并行化的特征筛选。
O b j ( t ) ≃ ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T = ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T \begin{aligned} Obj^{(t)} & \simeq \sum_{j=1}^{T}\left[(\sum_{i \in I_j}g_i)w_j+\frac{1}{2}(\sum_{i \in I_j}h_i+\lambda)w_j^2\right]+\gamma T \\ & = \sum_{j=1}^{T}\left[G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2\right]+\gamma T \end{aligned} Obj(t)≃j=1∑T⎣⎡(i∈Ij∑gi)wj+21(i∈Ij∑hi+λ)wj2⎦⎤+γT=j=1∑T[Gjwj+21(Hj+λ)wj2]+γT
4.3 Split Finding Algorithms
- 论文的核心之一,是xgb跑的快的原因。
4.3.1 Basic Exact Greedy Algorithm
- 精确的贪心算法
- 遍历所有可能的分割点
- 根据特征值对数据进行排序,并对数据进行排序访问
4.3.2 Approximate Algorithm
- 当数据量过大,传统算法就不好用了,因为要遍历每个分割点,甚至内存都放不下。所以,xgb提出了一种近似算法能加快运行时间。
- 该算法首先根据特征分布的百分位数提出(propose)候选分割点。有 global proposal 和 local proposal 两种
- global的是在建树之前就做proposal,然后每次分割都要更新一下proposal
- local的方法是在每次split之后更新proposal。
4.3.3 Weighted Quantile Sketch(加权分位数略图)
4.3.4 Sparsity-aware Split Finding
- 在分割的时候,xgb系统还能感知稀疏值,给每个树的结点都加了一个默认方向
- 当一个值是缺失值时,就把它分类到默认方向,每个分支有两个选择,枚举向左和向右的情况,哪个gain大选哪个
4.4 System Design
- 论文重中之重
4.4.1 Column Block for Parallel Learning(并行化)
- 树学习最耗时的部分是数据排序
- 为了降低排序成本,将数据存储在内存单元中,称之为块
- 每个块中的数据以压缩列格式存储,每个列按相应的特征值排序。
- 这个输入数据布局只需要在训练之前计算一次,并且可以在以后的迭代中重用。
- 可以使用多个块,每个块对应于数据集中的行的子集。
- 不同的块可以分布在不同的机器上,也可以在内核外存储在磁盘上。
- 使用排序结构,分位数查找步骤将成为对排序列的线性扫描。
- 直方图聚集中的二值搜索也成为一种线性时间合并算法。
对每列的统计数据进行并行采集,给出了一种并行的分割查找算法。重要的是,列块结构还支持列子采样,因为很容易在块中选择列的子集。
【特征选择时,并行处理列数据,XGB就是在这实现的并行化,多线程实现加速】
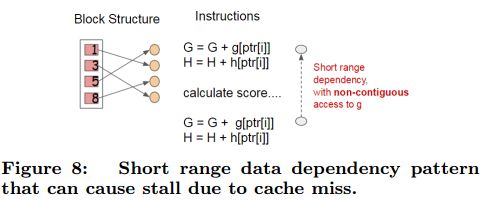
4.4.2 Cache-aware Access
- 当数据排序后,索引值是乱序的,可能指向了不同的内存地址
- 找的时候数据是不连续的,这里加了个缓存,让以后找的时候能找到小批量的连续地址,以实现加速
4.4.3 Blocks for Out-of-core Computation
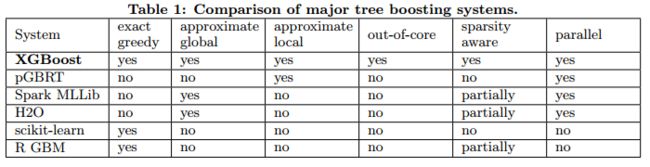
4.5 Related Works
4.6 End to End Evalutions
column subsampling表现不太稳定,sub有时好有时不好,什么时候该用sub呢?当没有重要的特征要选,每个特征值的重要性都很平均的时候,对列的subsampling效果就比较差了。
分布式的实验:在Amazon的云服务平台上用了32台m3.2xlarge搭建了一个YARN集群,数据没有放在HDFS里,放在了Amazon的S3 storage上,xgb虐了spark MLLib。
5. XGBoost 调参
5.1 XGBoost优点
- 正则化:控制模型复杂度,防止过拟合。
- 并行处理:不是tree粒度,特征粒度。特征排序最耗时,预排序后保存为block结构。
- 灵活性:可自定义目标函数,只要满足二阶可导。
- 缺失值处理:自动学习分裂方向
- 剪枝:先建立所有可以建立的子树,再从底到顶反向剪枝。
- 内置交叉验证:允许在每一轮boosting迭代中使用交叉验证,获得最迭代次数
5.2 XGBoost参数详解
三部分:通用参数,tree booster参数,学习目标参数
5.2.1 通用参数
- booster:可选gbtree和gblinear
- silent:取0打印运行时信息,取1不打印
- nthread:运行时的线程数
- num_pbuffer:预测结果缓冲区大小,保存最后一步提升的预测结果
- num_feature:Boosting过程中用到的特征维数
5.2.2 tree booster参数
- eta:收缩步长,类似于学习率,默认0.3
- gamma:节点分裂时,只有分裂后损失函数的值下降了,才会分裂这个节点,用于控制是否后剪枝
- max_depth:树的最大深度,默认为6,交叉验证调优
- min_child_weight :孩子节点中最小的样本权重和。如果叶子节点的样本权重和小于该值则拆分过程结束。用于避免过拟合,但是过高会导致欠拟合
- subsample :训练模型的子样本占整个样本集合的比例。随机抽取子样本建立树模型,防止过拟合
- colsample_bytree:对特征采样的比例
- lambda,alpha:Linear Booster时的L2、L1正则化参数
5.2.3 学习目标参数
- objective:可选 reg:linear,reg:logistic,binary:logistic,multi:softmax等
- base_score:所有实例样本的初始化预测分数,全局偏置,默认0.5
- eval_metric:可选 mse,mae,logloss,error,merror,auc
- seed:随机数种子
5.2.4 XGBoost基本方法和默认参数
params = {
'booster': 'gbtree',
'objective': 'multi:softmax',
'num_class': 10,
'gamma': 0.1,
'max_depth': 6,
'lambda': 2,
'subsample': 0.7,
'colsample_bytree': 0.7,
'min_child_weight': 3,
'silent': 1,
'eta': 0.007,
'seed': 1000,
'nthread': 4,
}
xgboost.train(params,
dtrain,
num_boost_round=10,
evals=(),
obj=None,
feval=None,
maximize=False,
early_stopping_rounds=None,
evals_result=None,
verbose_eval=True,
learning_rates=None,
xgb_model=None)
- params :字典形式,参数
- dtrain :训练数据
- num_boost_round:提升迭代个数
- evals :列表形式,训练过程中评估列表中的元素。如evals = [(dtrain,’train’), (dval,’val’)]
- obj:自定义目标函数
- feval:自定义评估函数
- maximize: 是否对评估函数进行最大化
- early_stopping_rounds: 早停次数 ,假设为100,验证集误差在100次迭代内不再继续降低,就停止迭代。
- evals_result :字典,存储在watch_list 中元素的评估结果。
- verbose_eval:如果为True, evals中元素的评估结果会输出在结果中; 如果输入数字,假设为5,则每隔5个迭代输出一次。
- learning_rates :每一次提升的学习率列表
- xgb_model:训练之前用于加载的xgb
model
6. XGBoost接口
6.1 XGBoost原生接口——分类问题
from sklearn.datasets import load_iris
import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载样本数据集
iris = load_iris()
X,y = iris.data,iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
# 算法参数
params = {
'booster': 'gbtree',
'objective': 'multi:softmax',
# 'objective': 'reg:gamma', # 回归问题目标函数
'num_class': 3,
'gamma': 0.1,
'max_depth': 6,
'lambda': 2,
'subsample': 0.7,
'colsample_bytree': 0.7,
'min_child_weight': 3,
'silent': 1,
'eta': 0.1,
'seed': 1000,
'nthread': 4,
}
plst = params.items()
# 生成数据集格式
dtrain = xgb.DMatrix(X_train, y_train)
dtest = xgb.DMatrix(X_test)
# xgboost模型训练
num_rounds = 500
model = xgb.train(plst, dtrain, num_rounds)
# 对测试集进行预测
y_pred = model.predict(dtest)
accuracy = accuracy_score(y_test,y_pred)
print("accuarcy: %.2f%%" % (accuracy*100.0))
# 显示重要特征
plot_importance(model)
plt.show()
6.2 XGBoost的sklearn接口——分类问题
from sklearn.datasets import load_iris
import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 加载样本数据集
iris = load_iris()
X,y = iris.data,iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
# 训练模型
model = xgb.XGBClassifier(max_depth=5, learning_rate=0.1, n_estimators=160, silent=True, objective='multi:softmax')
model.fit(X_train, y_train)
# 对测试集进行预测
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test,y_pred)
print("accuarcy: %.2f%%" % (accuracy*100.0))
# 显示重要特征
plot_importance(model)
plt.show()
6.3 XGBoost 调参经验
(1)先给定以下参数初始值,CV调整决策树数量
- max_depth=6
- min_child_weight=1
- gamma=0
- subsample=0.8
- colsample_bytree=0.8
- learning_rate=0.1
(2)调优 max_depth,min_child_weight
- 这两个参数对结果影响最大
- 先大范围粗调,再小范围微调
(3)依次 gamma,subsample ,colsample_bytree 参数调优
(4)正则化参数调优
(5)降低学习率,使用更多的决策树
参考博客
1. python机器学习案例系列教程——GBDT算法、XGBOOST算法
2. Boosting学习笔记(Adboost、GBDT、Xgboost)
3. xgboost原理
4. XGBoost 论文翻译+个人注释