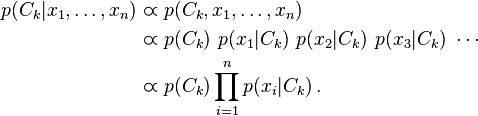PGM:概率图模型Graphical Model
http://blog.csdn.net/pipisorry/article/details/51461878
概率图模型Graphical Models简介
完全通过代数计算来对更加复杂的模型进行建模和求解。然而,我们会发现,使用概率分布的图形表示进行分析很有好处。这种概率分布的图形表示被称为概率图模型( probabilistic graphical models )。
这些模型提供了几个有用的性质:
• 它们提供了一种简单的方式将概率模型的结构可视化,可以用于设计新的模型。
• 通过观察图形,我们可以更深刻地认识模型的性质,包括条件独立性质。
• 高级模型的推断和学习过程中的复杂计算可以根据图计算表达,图隐式地承载了背后的数学表达式。
为什么要引入概率图模型?
对于一般的统计推断问题,概率模型能够很好的解决,那么引入概率图模型又能带来什么好处呢?
LDPC码的译码算法中的置信传播算法的提出早于因子图,这在一定程度上说明概率图模型不是一个从不能解决问题到解决问题的突破,而是采用概率图模型能够更好的解决问题。《模式识别和机器学习》这本书在图模型的开篇就阐明了在概率模型中运用图这一工具带来的一些好的性质,包括
1. They provide a simple way to visualize the structure of a probabilistic model and can be used to design and motivate new models.
2. Insights into the properties of the model, including conditional independence properties, can be obtained by inspection of the graph.
3. Complex computations, required to perform inference and learning in sophisticated models, can be expressed in terms of graphical manipulations, in which underlying mathematical expressions are carried along implicitly.
简而言之,就是图使得概率模型可视化了,这样就使得一些变量之间的关系能够很容易的从图中观测出来;同时有一些概率上的复杂的计算可以理解为图上的信息传递,这是我们就无需关注太多的复杂表达式了。最后一点是,图模型能够用来设计新的模型。所以多引入一数学工具是可以带来很多便利的,我想这就是数学的作用吧。
PGM的结构是从以下三点来进行的
Reprentation:如何建模以表示现实世界中的不确定性和各个量之间的关系。
Inference:如何从我们建立的模型中去推知我们要求的问题(概率).
Learnig:对于我的数据来说,什么模型是相对正确的?
这一思路致力于建立一个解决问题的框架,很多机器学习算法可以从这一框架下来理解。
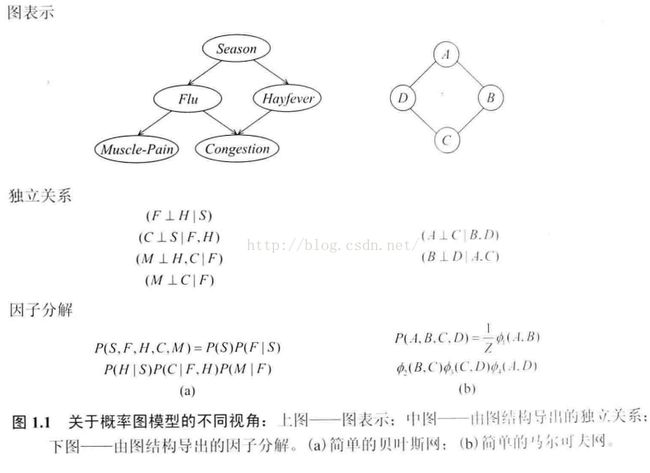
结构化概率模型
概率图模型
Note: 这种断言并不代表季节与充血是独立的!
表示、推理和学习概述
...
[《Probabilistic Graphical Models:Principles and Techniques》(以下简称PGM)]
皮皮blog
Graphical Model的基本类型
它们的主要区别在于采用不同类型的图来表达变量之间的关系:贝叶斯网络采用有向无环图(Directed Acyclic Graph)来表达因果关系,马尔可夫随机场则采用无向图(Undirected Graph)来表达变量间的相互作用。
这种结构上的区别导致了它们在建模和推断方面的一系列微妙的差异。一般来说,贝叶斯网络中每一个节点都对应于一个先验概率分布或者条件概率分布,因此整体的联合分布可以直接分解为所有单个节点所对应的分布的乘积。
而对于马尔可夫场,由于变量之间没有明确的因果关系,它的联合概率分布通常会表达为一系列势函数(potential function)的乘积。通常情况下,这些乘积的积分并不等于1,因此,还要对其进行归一化才能形成一个有效的概率分布——这一点往往在实际应用中给参数估计造成非常大的困难。
一个图由结点( nodes )(也被称为端点( vertices ))和它们之间的链接( links )(也被称为边( edges )或弧( arcs ))组成。在概率图模型中,每个结点表示一个随机变量(或一组随机变量),链接表示这些变量之间的概率关系。这样,图描述了联合概率分布在所有随机变量上能够分解为一组因子的乘积的方式,每个因子只依赖于随机变量的一个子集。
贝叶斯网络( Bayesian network ),也被称为有向图模型( directed graphical model )。这个模型中,图之间的链接有一个特定的方向,使用箭头表示。
另一大类图模型是马尔科夫随机场( Markov random fields ),也被称为无向图模型( undirected graphical models )。这个模型中,链接没有箭头,没有方向性质。
有向图对于表达随机变量之间的因果关系很有用,而无向图对于表示随机变量之间的软限制比较有用。
为了求解推断问题,通常比较方便的做法是把有向图和无向图都转化为一个不同的表示形式,被称为因子图( factor graph )。
有向图模型(贝叶斯网络)
举个例子,譬如有一组变量![]() ,如果每个变量只与其前一个变量有关(1阶马尔可夫过程),那么以下等式成立
,如果每个变量只与其前一个变量有关(1阶马尔可夫过程),那么以下等式成立
![]()
那么如何用图来表示这一关系呢?自然,我们要表示的是右边的式子,右边的式子表示了变量之间的联系。而当我们观察条件概率时,我们发现我们必须要指明哪个是条件。如果我们采用变量为节点,采用无向图这种节点等价的关系显然不能直接描述条件概率,因此这里选择了有向图来描述这一关系,即![]() 表示为
表示为
那么此时上述的1阶马尔可夫过程表示为,注意其中没有箭头指向![]() ,故表示
,故表示![]() 意味着无条件。
意味着无条件。
有向图模型,或称贝叶斯网络,描述的是条件概率,或许这就是其被称为贝叶斯网络的原因吧。此处不再细说,更多内容(包括d-separation等)可参考后文提及的相关资料。
无向图模型(马尔可夫随机场)
构造有向图模型需要变量之间显式的、很强的约束关系。即首先要有条件概率分布关系,其次还要是可求的。为了达到这一目的,很有可能我们要做很多不切实际的假设。譬如朴素贝叶斯(Naive Bayes)的假设就相当的Naive。如下所示,其假设往往是不成立的。
那什么是更弱的假设呢?很多时候我们知道两个变量之间一定是相关的,但我们不知道到底是怎么相关的。这时候我们也可以用其相关性来构造概率图模型。相关是不分方向的,此时我们应该选择无向图来表示。
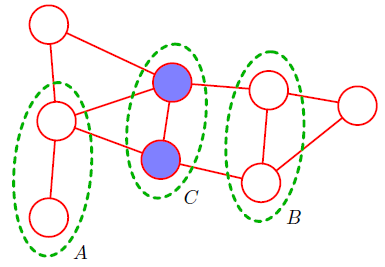
和相关对应的是独立(实际上是不相关,这里不做区分了),我们可以这样来构造图模型,如果两个节点之间独立,那么没有路使其相连。条件独立即去掉条件中节点后,两节点之间没有路相连。具体可由《PATTERN RECOGNITION and MACHINE LEARNING》中的例子阐述
如上图所示,A中节点到B集合中节点的每一条路都通过了C中节点,这代表着![]() 。无向图模型很完美的将这种弱的关系表现出来了,有一种很神奇的感觉,但光表示是没有多大用处的,我们还是要计算概率。对于变量
。无向图模型很完美的将这种弱的关系表现出来了,有一种很神奇的感觉,但光表示是没有多大用处的,我们还是要计算概率。对于变量![]() ,显然有
,显然有![]()
但更显然的是我们不应该这样做,因为没有意义。所以他们是这样做的,为什么可以?我也没弄明白,我只是感觉了一下,觉得差不多……思想是一样的,就是把概率分开,分开了才能体现特点。
将图中的节点分成多个小的集合Xc
,其中集合内的点两两之间有边相连接,这些集合被称为cliques,那么概率分布满足
其中Z
是归一化因子(使得概率之和为1), Φ函数是势能函数,恒正。取为
![]()
![]() 是能量函数,不得不说这是一个很神奇的东西。不太会就先总结到这里了。
是能量函数,不得不说这是一个很神奇的东西。不太会就先总结到这里了。
因子图
按理来说,无向+有向就全了。为什么还有一类呢?或许严格来说不应该将因子图和上述两类并列的,但我不知道放到哪里去……
因子,从名字中就强调了的两个字一定是其重要组成部分。而上述的两类图表现出的变量之间最终的关系实际上就是将概率分布化为了多个式子的乘积。对于多项式而言,我们有因式分解。譬如在解高次方程的时候,我们非常希望方程能够分解为多个低次方程的乘积。那么,对于概率分布函数而言,我们也希望能够这样做,即
![]()
其中,![]() 是
是![]() 中变量的子集,至于到底能够如何分解是取决于问题的,就好象多项式的分解取决于其具体形式。对于一个实际的问题,如果有以下关系
中变量的子集,至于到底能够如何分解是取决于问题的,就好象多项式的分解取决于其具体形式。对于一个实际的问题,如果有以下关系
![]()
那么这一个式子的因子图表示如下
从这个例子,我们总结一下因子图是什么。因子图有两类节点,一是变量节点,另一类为因子节点。这两类节点的内部没有边直接相连,变量的概率分布可以因式分解为因子节点的函数的乘积,因子节点的函数变量包括与其直接相连的变量节点。
三类图各有特点,适用于不同的场合,且这三类图是可以相互转换的。转换方式此处不做描述。
Graphical Model的新发展方向
Probabilistic Graphical Model的另外一个重要的发展方向是非参数化。与传统的参数化方法不同,非参数化方法是一种更为灵活的建模方式——非参数化模型的大小(比如节点的数量)可以随着数据的变化而变化。一个典型的非参数化模型就是基于狄利克莱过程(Dirichlet Process)的混合模型。这种模型引入狄利克莱过程作为部件(component)参数的先验分布,从而允许混合体中可以有任意多个部件。这从根本上克服了传统的有限混合模型中的一个难题,就是确定部件的数量。在近几年的文章中,非参数化模型开始被用于特征学习。在这方面,比较有代表性的工作就是基于Hierarchical Beta Process来学习不定数量的特征。
皮皮blog
基于Graphical Model 的统计推断 (Inference)
主流的近似推断方法有三种:
Jason Johnson等人在2005年建立的walk sum analysis为高斯马尔可夫随机场上的belief propagation提供了系统的分析方法。这种方法成功刻画了belief propagation在高斯场上的收敛条件,也是后来提出的多种改进型的belief propagation的理论依据。 Thomas Minka在他PhD期间所建立的expectation propagation也是belief propagation的在一般Graphical Model上的重要推广。
[【综述】(MIT博士)林达华老师-"概率模型与计算机视觉”]
from: http://blog.csdn.net/pipisorry/article/details/51461878
ref: [《Probabilistic Graphical Models:Principles and Techniques》(以下简称PGM)]
[概率图模型简介《An introduction to graphical models》 Kevin P. Murphy]