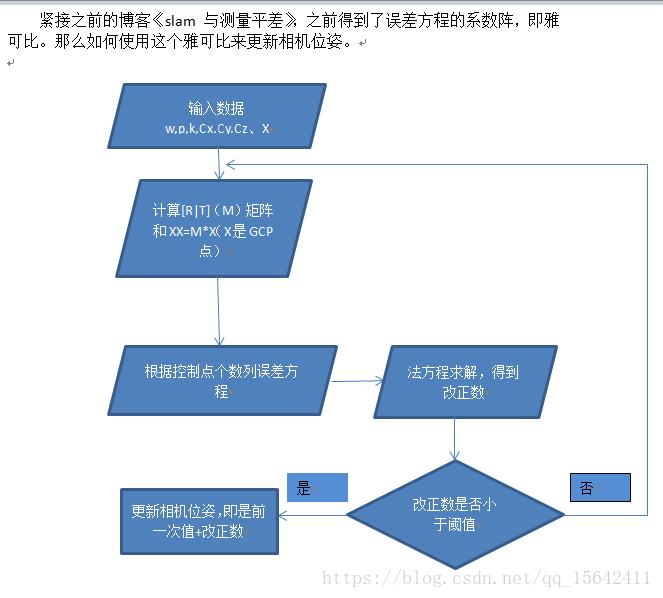
高斯牛顿法--slam 迭代求解相机位姿
代码如下:
# -*- coding: utf-8 -*-
from sympy import *
import numpy as np
w,p,k=symbols("w,p,k")#角元素
Cx,Cy,Cz=symbols("Cx,Cy,Cz")#线元素
X,Y,Z,f=symbols("X,Y,Z,f") #控制点坐标和f
def make_rotation_matrix(alpha,beta,gamma):
A_x = np.array([[1,0,0],
[0,cos(alpha),-sin(alpha)],
[0,sin(alpha),cos(alpha)]])
A_y = np.array([[cos(beta),0,sin(beta)],
[0,1,0],
[-sin(beta),0,cos(beta)]])
A_z = np.array([[cos(gamma),-sin(gamma),0],
[sin(gamma),cos(gamma),0],
[0,0,1]])
A = np.dot( np.dot(A_z,A_y), A_x )
return A
R=make_rotation_matrix(w,p,k)
R=Matrix(R)
C=Matrix([[-Cx],[-Cy],[-Cz]])
t=R*C
M=Matrix(np.hstack((R,t)))
PP=M*Matrix([[X],[Y],[Z],[1]])
#误差方程系数即是雅可比系数(CV中的误差方程系数)
a11=-f/PP[2] #delta Cx
a12=0 #delta Cy
a13=f*PP[0]/PP[2]**2 #delta Cz
a14=f*PP[0]*PP[1]/PP[2]**2 #delta w
a15=-(f+f*PP[0]**2/PP[2]**2) #delta p
a16=f*PP[1]/PP[2]
#Vx=a11*deltaCx+a12*deltaCy+a13*deltaCz+a14*deltaw+a15*deltap+a16*deltak
b11=0
b12=-f/PP[2]
b13=f*PP[1]/PP[2]**2
b14=f+f*PP[1]**2/PP[2]**2
b15=-f*PP[0]*PP[1]/PP[2]**2
b16=-f*PP[0]/PP[2]
#Vy=b11*deltaCx+b12*deltaCy+b13*deltaCz+b14*deltaw+b15*deltap+b16*deltak
#假设有n个控制点,则误差方程系数阵位2n*6
'''
Cx=Cx+deltaCx
Cy=Cy+deltaCy
Cz=Cz=deltaCz
w=w+deltaw
p=p+deltap
k=k+deltak
初值有SFM 算法得到
迭代求解改正数,若改正数小于某一阈值,如deltak<0.01,终止
'''