遗传算法解决TSP问题

基本原理

Holland的模式定理提出，遗传算法的实质是通过选择、交配和变异算子对模式进行搜索，低阶、定义长度较小且平均适应值高于群体平均适应值的模式在群体中的比例将呈指数级增长。即随着进化的不断进行，较优染色体的个数将快速增加。

模式定理

模式：指群体中编码的某些位置具有相似结构的染色体集合
模式的阶：指模式中具有确定取值的基因个数
模式的定义长度：指模式中第一个具有确定取值的基因到最后一个具有确定取值的基因的距离

遗传算法的基本问题

• 染色体的编码

• 群体的初始化

• 适应值评价

• 选择种群

• 种群交配

• 种群变异

1.染色体编码

染色体的编码也就是问题解的表示，染色体编码的确定会对接下来的交配和变异构成影响。目前常用的两种简单的编码方式：二进制编码和浮点数编码。在含有多变量的优化问题或对精度要求较高时寻求浮点数编码方法。

2.群体初始化

一般情况下，遗传算法在群体初始化阶段采用的是随机数初始法，采用生成随机数的方法对染色体每一维变量进行初始化赋值。（如果在初始化阶段已经保证种群是优良群体的话，将有效提高算法找到全局最优解的能力。

3.适应值评价

采用评估函数区分染色体的优劣。在遗传算法中，规定适应值越大的染色体越优。因此对于一些求解最大值的数值优化问题，我们可以直接套用问题定义的函数表达式。但是对于其他优化问题，问题定义的目标函数表达式必须经过一定的变换。

4.选择算子

种群的选择操作使用轮盘赌注算法，其基本思想是概率的随机选择。
1）根据群体中的每个染色体的适应值得到整个群体的适应值总和。
2）分别计算每个染色体的适应值与总适应值之比Pi。
3 )假设一个轮盘有N个扇区，每个染色体对应一个扇区，每个扇区的大小与Pi成正比。
4）每转动一次轮盘，轮盘停止时指向的扇区为被选中进入种群的群体。
5）进行N次选择即可得到同样规模为N的种群。

从轮盘的赌注机制可以看到，较优染色体的P值较大，被选中的可能性也越大。但由于过程的选择具有随机性，也给予了较差染色体一定的生存空间。

5.交配算子

在染色体交配阶段，每个染色体能否进行交配由交配概率Pc（一般取值为0.4到0.99之间）决定，其具体过程为：对于每个染色体，如果Random(0, 1)小于Pc则表示该染色体可进行交配操作（其中Random(0, 1)为[0, 1]间均匀分布的随机数），否则染色体不参与交配直接复制到新种群中。

每两个按照Pc交配概率选择出来的染色体进行交配，经过交换各自的部分基因，产生两个新的子代染色体。具体操作是随机产生一个有效的交配位置，染色体交换位于该交配位置后的所有基因。

6.变异算子

染色体的变异作用于基因之上，对于交配后新种群中染色体的每一位基因，根据变异概率Pm判断该基因是否进行变异。如果Random(0, 1)小于Pm，则改变该基因的取值（其中Random(0, 1)为[0, 1]间均匀分布的随机数）。否则该基因不发生变异，保持不变。

遗传算法的流程

基于遗传算法的旅行商问题

1.初始群体的设定
定义一个s行t列的pop矩阵来表 示群体， t 为城市个数 ，即 N ， s 为样本中个 体数目。在本文探讨了 10 个城市的 TSP 问题，此 时 t 取值 10，该矩阵中每一行的前10 个元素表示 经过的城市编号，并且另设置一维向量代表每个个体的适应度（每个个体所求的距离）。

//初始化种群
    public void init(){

        //该矩阵中每一行的前N个元素表示 经过的城市编号，
        group=new int[gen][N];

        //随机初始化 
        for(int i=0;inew boolean[N];
            for(int p=0;pfalse;
            }
            for(int j=0;jnew Random();

            while(true){
            int randInt = rand.nextInt(10);
            if(visit[randInt]==false){
                visit[randInt]=true;
                group[i][j]=randInt;
                break;
            }
            }

            }
        }
    }

2.适应度函数的计算
用距离的总和作为适应度函数，来衡量求解结果是否最优。

//初始化dist[][]
    public void initDist(double[][] coordinate){
        dist = new double[N][N];
        for(int i=0;ifor(int j=0;jif(i!=j){
                    double tempx = coordinate[i][0]-coordinate[j][0];
                    double tempy = coordinate[i][1]-coordinate[j][1];
                    dist[i][j]=Math.sqrt(Math.pow(tempy, 2)+Math.pow(tempx, 2));
                }else{
                    dist[i][j]=0;
                }
            }
        }
    }

3.选择指以一定的概率从群体中选择优胜个体的操作，它是建立在群体中个体适应度评估基础上的。为了加快局部搜索的速度，在算法中采用最优保存策略的方法，即将群体中适应度最大的个体直接替换适应度最小的个体。它们不进行交叉和变异运算，而是直接复制到下一代，以免交叉 和变异运算破坏种群中的优秀解答。

    //选择算子，用适应度最大的算子替代最小的算子，直接复制到下一代
    public void select(){
        //计算适应值总和
        double total = 0;
        for(int i=0;iout.println("适应值总和为:"+total);

        //计算适应值比率
        double[] part = new double[gen];
        for(int i=0;ifor(int i=0;iout.println("第"+i+"个个体适应值为:"+part[i]);
        }

        int worstChoice = -1;
        int bestChoice = -1;
        double best = Double.MIN_VALUE;
        double worst = Double.MAX_VALUE;
        for(int i=0;iif(bestif(worst>part[i]){
                worstChoice=i;
                worst=part[i];
            }
        }
        System.out.println("最大适应值的个体为:"+bestChoice);
        System.out.println("最小适应值的个体为:"+worstChoice);

        for(int i=0;igroup[bestChoice][i];
            newGroup[worstChoice][i]=group[worstChoice][i];
        }
        }

4.交配算子
交叉算子是产生新个体的主要手段。它是指将个体进行两两配对，以交叉概率 Pc 将配对的父代个体的部分结构加以替换重组生成新个体的操作本文中采用有序交叉法来实现。

有序交叉法的步骤描述如下:
第一步: 以交叉概率随机地选择两个交叉点;
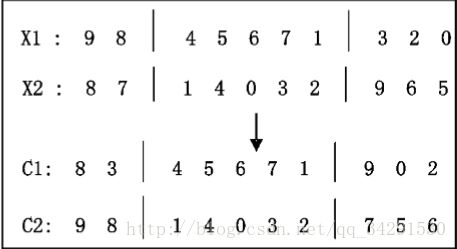
第二步: 按对应位置复制双亲 X1 和 X2 匹配 段中的两个子串 Y1 和 Y2;
第三步: 在对应位置交换双亲匹配段以外的 子串，如果交换后，后代 C1 中的某一城市与子串 Y1中的城市重复，则将该城市取代为子串Y2中与 Y1 中的该城市具有相同位置的新城市，直到与子 串 Y1 中的城市均不重复为止，对后代 C2 也采用 同样的方法，如图 2 所示。

关于有序交叉（Order Crossover)可以参考另一篇博客：
http://blog.csdn.net/u012750702/article/details/54563515

//交配算子 有序交叉
    public void crossover(){

        for(int i=0;iif(copulation[i]==true){
                Random rand = new Random();
                double tempRand= rand.nextDouble();
                if(tempRand>PC){    //不参加交配
                    copulation[i]=false;
                }
            }
        }

        for(int i=0;iif(copulation[i]==true)
            System.out.println("个体"+i+"参加交配");
        }

        //两两交配
        int parent1=-1;
        int parent2=-1;

        for(int i=0;iif(copulation[i]==true){
                if(parent1==-1){
                    parent1=i;
                }else{
                    parent2=i;
                    //开始交配
                    //选择两个交叉点
                    int crossIndex1=0;
                    int crossIndex2=0;

                    while(true){
                        Random rand = new Random();
                        crossIndex1=rand.nextInt(10);
                        crossIndex2=rand.nextInt(10);
                        if(crossIndex1!=crossIndex2){
                            break;
                        }
                    }
                    int temp = crossIndex2;
                    crossIndex2=crossIndex1>crossIndex2?crossIndex1:crossIndex2;
                    if(temp!=crossIndex2){
                        crossIndex1=temp;
                    }


                    //将交叉点之间的基因复制到下一代染色体中
                    for(int j=crossIndex1;jgroup[parent1][j];
                        newGroup[parent2][j]=group[parent2][j];
                    }


                    boolean[] exist1 = new boolean[N];
                    boolean[] exist2 = new boolean[N];

                    for(int p=0;pboolean flag = false;
                        for(int q=crossIndex1;qif(group[parent2][p]==group[parent1][q]){
                                flag = true;
                            }
                        }
                        exist2[p]=flag;
                    }

                    for(int p=0;pboolean flag = false;
                        for(int q=crossIndex1;qif(group[parent1][p]==group[parent2][q]){
                                flag = true;
                            }
                        }
                        exist1[p]=flag;
                    }


                    //子代1的产生
                    int index2=0;
                    for(int index1=0;index1for(;index2if(exist2[index2]==false){      //将该处的基因复制到子代
                                newGroup[parent1][index1]=group[parent2][index2];
                                ++index2;
                                break;
                            }
                        }
                    }

                    for(int index1=crossIndex2;index1for(;index2if(exist2[index2]==false){      //将该处的基因复制到子代
                                newGroup[parent1][index1]=group[parent2][index2];
                                ++index2;
                                break;
                            }
                        }
                    }
                    //子代2的产生
                    int i2=0;
                    for(int index1=0;index1for(;i2if(exist1[i2]==false){      //将该处的基因复制到子代
                                newGroup[parent2][index1]=group[parent1][i2];
                                ++i2;
                                break;
                            }
                        }
                    }

                    for(int index1=crossIndex2;index1for(;i2if(exist1[i2]==false){      //将该处的基因复制到子代
                                newGroup[parent2][index1]=group[parent1][i2];
                                ++i2;
                                break;
                            }
                        }
                    }
                    parent1=-1;
                    parent2=-1;
                }
            }
        }
        //如果还有一个染色体没有交配，直接复制到子代
        if(parent1!=-1&&parent2==-1){
            for(int i=0;igroup[parent1][i];
            }
        }

    }

5.变异算子

变异操作是以较小的概率 Pm 对群体中个体编码串上的某位或者某些位作变动，从而生成新 的个体。本文中采用倒置变异法: 假设当前个体 X 为( 1 3 7 4 8 0 5 9 6 2) ，如果当前随机概率值小 于 Pm，则随机选择来自同一个体的两个点 mutatepoint( 1) 和 mutatepoint( 2) ，然后倒置两点 的中间部分，产生新的个体。 

//变异算子 倒置变异法
    public void mutate(){
        for(int index=0;indexindex){
            if(mutation[index]==true){
        //产生随机数 判断是否需要变异
        Random r = new Random();
        double m=r.nextDouble();
        if(m>PM){   //不需要变异
           mutation[index]=false;
        }
        }
    }

        for(int index=0;indexindex){
            if(mutation[index]==true){
                System.out.println("变异算子:"+index);
                int index1=0;
                int index2=0;
            while(true){
                Random rand = new Random();
                index1=rand.nextInt(10);
                index2=rand.nextInt(10);
                if(index1!=index2){
                    break;
                }
            }
            int temp = index2;
            index2=index2>index1?index2:index1;
            if(index2!=temp){
                index1=temp;
            }
        //倒置index1与indexe2之间的基因
        for(int i=index1;iint t = newGroup[index][i];
            newGroup[index][i]=newGroup[index][index2-i];
            newGroup[index][index2-i]=t;
        }
        }
    }

}

6.构造算法流程

public static void main(String args[]){
        double[][] coordinate = {
                {0.4000,0.4439},
                {0.2439,0.1463},
                {0.1707,0.2293},
                {0.2293,0.7610},
                {0.5171,0.9414},
                {0.8732,0.6536},
                {0.6878,0.5219},
                {0.8488,0.3609},
                {0.6683,0.2536},
                {0.6159,0.2623}
        };
        Genetic ge = new Genetic();
        ge.setGen(5);
        ge.initDist(coordinate);
        ge.init();
        ge.evaluate();
        for(int i=0;i<500;++i){
        ge.select();
        ge.crossover();
        ge.mutate();
        ge.evaluate();
        }
    }

7.实验结果

0 6 7 8 3 4 1 2 5 9 
4 0 7 2 8 3 6 1 9 5 
8 2 5 7 9 6 0 1 3 4 
3 5 2 0 8 7 6 9 4 1 
5 3 6 1 2 4 9 7 8 0 
变异算子:4
倒置后:
0 6 7 8 3 4 1 2 5 9 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
3 5 2 0 8 7 6 9 4 1 
0 3 6 1 2 4 9 7 8 5 
倒置后:
0 6 7 8 3 4 1 2 5 9 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
0 3 6 1 2 4 9 7 8 5 
倒置后:
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
0 3 6 1 2 4 9 7 8 5 
倒置后:
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
倒置后:
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4 
8 2 5 7 9 6 0 1 3 4