深度学习进阶之（一）AutoEncoder

1. AutoEncoder的原理、变种及实现

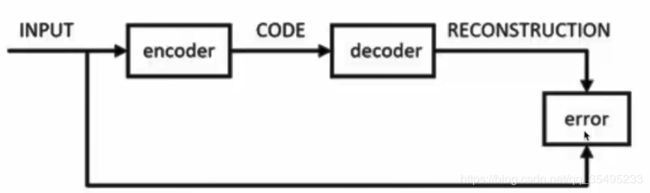
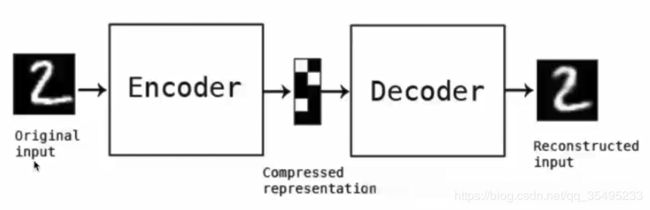
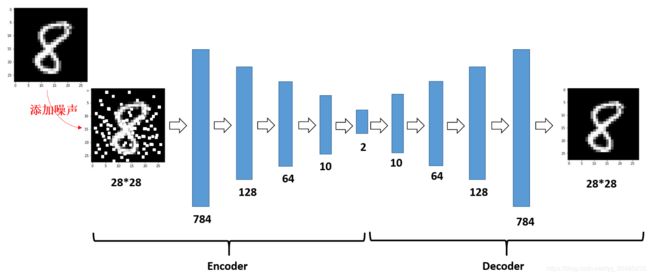
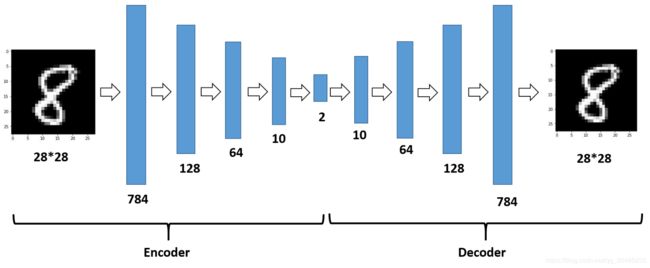
          AutoEncoder包含输入层、隐含层以及输出层，AutoEncoder原理就是利用BP来进行整个过程，那么如何构建AutoEncoder呢？

1.搭建编码器

2.搭建解码器

3. 定义Loss function

         AutoEncoder主要用来数据去噪、为可视化降维以及构建深层神经网络。

                                         

                                                     

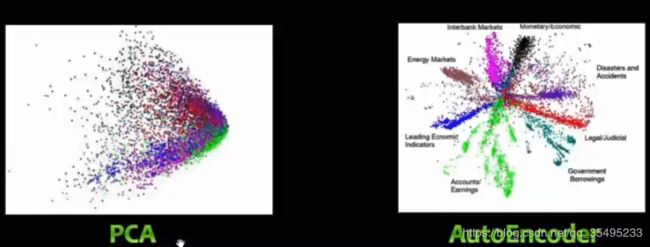
2. AutoEncoder与PCA的区别

      相同点：

         * 降维，作为特征提取器

      不同点：

         * PCA只能线性变换，AutoEncoder可以进行非线性变换

      降维的重点就是保证不要丢失太多的信息，我们使用主成分分析，假设原数据是n，我们把数据从原特征空间变换到新的特征空间，在新的特征空间，我们就把每一个特征维度设置为一个主方向，我们可以把n个主方向按方差从大到小排列，选择前K个维度，但是PCA处理时，假设为2，降维为1，那么我们就会损失一定的数据信息，如果AutoEncoder层数为1时，那么就与PCA是一样的。若为非1层的AutoEncoder的话，我们可以堆叠n个层作为深度学习的预训练，我们可以在编解码之后加上非线性变换，通过减少误差来学习参数， 那么相对于非线性的情况，我们可以学习到更多的结果。对于非线性函数来说，PCA以及AutoEncoder会得到以下两种情况：

                                      

 

 

3. AutoEncoder的变种（一）

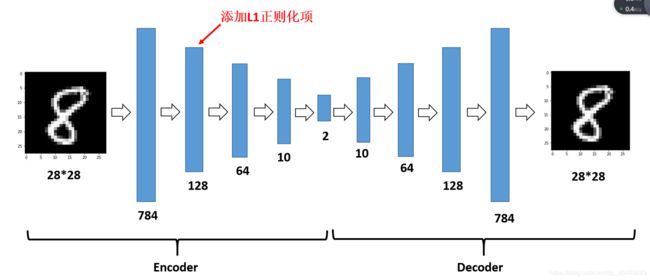
3.1 Sparse AutoEncoder

             Sparse AutoEncoder如下图所示：

                                                             

        Sparse中加入L1正则化或者KL散度，我们限制了每次表达的向量更加稀疏，因为稀疏的向量往往更有效。给隐藏的神经元加入稀疏性限制。在现实生活中，也正是有这种表达来满足我们的约束。简单来说，我们希望我们的模型越稀疏越好。这是一个非监督学习的过程，这是生成整个神经网络的预先训练的一种方法，通过初始化神经元来建立一个回归，这个回归来拟合我们的模型。当数据特征较高时，若我们不加稀疏性限制，就会抑制特征提取效果，因为Sparse本身就是一个正则项。详细代码可以参考本人的github：https://github.com/Merlin5417/AE-DAE-SDAE

                       

        增加了稀疏约束后的AutoEncoder的损失函数定义如下：

                                                                         

       KL表示KL散度，p表示网络中神经元的激活程度（若Activation为Sigmoid函数，此值可设为0.05，表示大部分神经元未激活），pj表示第j个神经元的平均激活程度。在此处，KL散度定义如下（KL散度实际上就是交叉熵加多一个常量）:

                                                                 

                                   

       KL散度衡量的是p与p平均这两个分布的分布情况，若KL散度算出来较小，那么就说明这两个分布越接近，若KL散度越大，说明这两个分布差距就越大。

       在这里，很多人会说稀疏性是什么？有什么好处？稀疏性指的是大多数神经元限制为0，只允许少量的神经元来激活，来达到“稀疏”的效果，这里的好处就是：

（1）有降维的效果，可以用于提取特征

（2）由于可以抓住主要特征，故具有一定抗噪能力

（3）稀疏的可解释性好，现实场景大多满足这种约束（如“奥卡姆剃刀定律”）

      通俗来说，就是将一个信号表示为一组基的线性组合，而且要求只需要较少的几个基就可以将信号表示出来。若激活函数为Sigmoid函数，其输出为-1，那么我们认为神经元是被抑制的，但是若Sigmoid输出为1，我们认为其是被激活的。所以说稀疏自编码就是将大多数神经元限制为0，只允许少数神经元来表达效果。

3.2 Denoising AutoEncoder

        降噪自编码就是为了增强我们模型的鲁棒性，在我们输入层加入噪声来进行训练，从而获得更好的模型泛化能力以及更强的鲁棒性。Denoising AutoEncoder模型如下：

                                                

         其以一定的概率将我们模型的输入层置语0，这有点类似神经网路的Dropout，给模型添加噪声。DAE的核心思想就是一个能够从恢复出原始信号的表达未必是最好的，能够对“被污染”的原始数据编码、解码，然后还能恢复真正的原始数据，这样的特征才是好的。

参考论文有：

* Extracting and composing robust features with denoising autoencoders.

* Stacked Denoising AutoEncoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion.

直观理解就是：

* Denosing AutoEncoder与人的感知机理类似，比如人眼看物体时，如果物体某一小部分被遮住了，人依然能够识别。

* 人在接受到多模态信息时（比如声音，图像等），少了其中某些模态信息有时也不会造成太大的影响。

* AutoEncoder的本质是学习一个相等的函数，即网络的输入和重构后的输出相等，这种相等函数的表示有个缺点就是当测试样本和训练样本不符合统一分布时，效果不好，而Denoising AutoEncoder在这方面的处理有所进步。

                       

      通常我们有三种加入噪声的方式：（1）加性高斯噪声（additive gaussian noise）；（2）掩模噪声（mask）；（3）椒盐噪声；

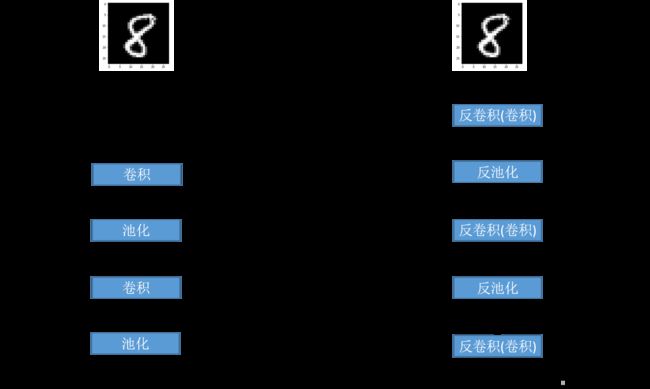
3.3 Convolutional AutoEncoder

                                             

3.4 Stacked AutoEncoder

                                   

3.5 LSTM AutoEncoder

                                      

3.6 Recursive AutoEncoder

3.7 Contractive AutoEncoder

                                          

4. 实例：AutoEncoder与聚类结合在预测用户偏好中的应用

       UseAutoEncoder在聚类实例中，例如在电商推荐中，举例有30万条数据，一共150种商品品类，1w个会员，特征仅仅只有用户的购买记录，但是我们希望根据用户的偏好进行分群，便于以后的推荐和预测。这里枚举例子如下：

cat sr_website.csv

      我们根据这个特征背景，我们这里截选会员id以及购买的物品消费的金额。

id	goods_name	goods_amount
xdr1ef	tj维达手卷纸	18.99
xdr1e2	tj清风原木纸巾（36）	29.99
xdr1e2	tj迪士尼精品购物袋	34.0
xdrket	tj泰国精品香米油	32.0
xdrkef	tj华为mate20 pro  4985.0
xdrkef	tj荣耀8x	1269.0
xdrkef	tjshes女饰胸针	86.0
xdkwve	tj清风原木纸巾（36）	29.99
xdkwve	tjswtp童装（中大童)	33.0
xdkwve	tj鳄鱼男士腰带	38.0

       由于一个id对应多个物品（一共假设150个特价商品），这样我们是无法进行一个特征训练的，这里我们需要将其进行特征处理成一个特征矩阵，每一列都是一个商品，每一行都是一个用户，之后转化成类似如下的矩阵：

#!/usr/bin/python
#coding:utf-8
#Author：Charlotte
import pandas as pd
import numpy as np
import time

#加载数据文件(你可以加载自己的文件，文件格式如上所示)
x=pd.read_table('test.txt',sep = "\t")

#去除NULL值
x.dropna()
a1=list(x.iloc[:,0])
a2=list(x.iloc[:,1])
a3=list(x.iloc[:,2])

#A是商品类别
dicta=dict(zip(a2,zip(a1,a3)))
A=list(dicta.keys())
#B是用户id
B=list(set(a1))

#创建商品类别字典
a = np.arange(len(A))
lista = list(a)
dict_class = dict(zip(A,lista))
#print dict_class

f=open('class.txt','w')
for k ,v in dict_class.items():
    f.write(str(k)+'\t'+str(v)+'\n')
f.close()

#计算运行时间
start=time.clock()

#创建大字典存储数据
dictall = {}
for i in xrange(len(a1)):
    if a1[i] in dictall.keys():
        value = dictall[a1[i]]
        j = dict_class[a2[i]]
        value[j] = a3[i]
        dictall[a1[i]]=value
    else:
        value = list(np.zeros(len(A)))
        j = dict_class[a2[i]]
        value[j] = a3[i]
        dictall[a1[i]]=value

#将字典转化为dataframe
dictall1 = pd.DataFrame(dictall)
dictall_matrix = dictall1.T
print dictall_matrix

end = time.clock()
print "赋值过程运行时间是:%f s"%(end-start)

cat data_matrix.txt |head

        
           0       1      2       3      4       5      6       7      8     9
xdr1ef   0.0  18.99    0.0     0.0    0.0     0.0    0.0     0.0    0.0   0.0
xdr1e2   0.0     0.0  29.99     0.0    0.0     0.0    0.0  34.0    0.0   0.0
xdrket   0.0     0.0    0.0     0.0    0.0     0.0    0.0     0.0  32.0   0.0
xdrkef  86.0     0.0    0.0     0.0    0.0  4985.0  1269.0     0.0    0.0   0.0
xdkwve   0.0     0.0    0.0     29.99  33.0     0.0    0.0     0.0    0.0  38.0

使用AutoEncoder进行降维：

#/usr/bin/python
#coding:utf-8

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing

class AutoEncoder():
    """ Auto Encoder  
    layer      1     2    ...    ...    L-1    L
      W        0     1    ...    ...    L-2
      B        0     1    ...    ...    L-2
      Z              0     1     ...    L-3    L-2
      A              0     1     ...    L-3    L-2
    """
    
    def __init__(self, X, Y, nNodes):
        # training samples
        self.X = X
        self.Y = Y
        # number of samples
        self.M = len(self.X)
        # layers of networks
        self.nLayers = len(nNodes)
        # nodes at layers
        self.nNodes = nNodes
        # parameters of networks
        self.W = list()
        self.B = list()
        self.dW = list()
        self.dB = list()
        self.A = list()
        self.Z = list()
        self.delta = list()
        for iLayer in range(self.nLayers - 1):
            self.W.append( np.random.rand(nNodes[iLayer]*nNodes[iLayer+1]).reshape(nNodes[iLayer],nNodes[iLayer+1]) ) 
            self.B.append( np.random.rand(nNodes[iLayer+1]) )
            self.dW.append( np.zeros([nNodes[iLayer], nNodes[iLayer+1]]) )
            self.dB.append( np.zeros(nNodes[iLayer+1]) )
            self.A.append( np.zeros(nNodes[iLayer+1]) )
            self.Z.append( np.zeros(nNodes[iLayer+1]) )
            self.delta.append( np.zeros(nNodes[iLayer+1]) )
            
        # value of cost function
        self.Jw = 0.0
        # active function (logistic function)
        self.sigmod = lambda z: 1.0 / (1.0 + np.exp(-z))
        # learning rate 1.2
        self.alpha = 2.5
        # steps of iteration 30000
        self.steps = 10000
        
    def BackPropAlgorithm(self):
        # clear values
        self.Jw -= self.Jw
        for iLayer in range(self.nLayers-1):
            self.dW[iLayer] -= self.dW[iLayer]
            self.dB[iLayer] -= self.dB[iLayer]
        # propagation (iteration over M samples)    
        for i in range(self.M):
            # Forward propagation
            for iLayer in range(self.nLayers - 1):
                if iLayer==0: # first layer
                    self.Z[iLayer] = np.dot(self.X[i], self.W[iLayer])
                else:
                    self.Z[iLayer] = np.dot(self.A[iLayer-1], self.W[iLayer])
                self.A[iLayer] = self.sigmod(self.Z[iLayer] + self.B[iLayer])            
            # Back propagation
            for iLayer in range(self.nLayers - 1)[::-1]: # reserve
                if iLayer==self.nLayers-2:# last layer
                    self.delta[iLayer] = -(self.X[i] - self.A[iLayer]) * (self.A[iLayer]*(1-self.A[iLayer]))
                    self.Jw += np.dot(self.Y[i] - self.A[iLayer], self.Y[i] - self.A[iLayer])/self.M
                else:
                    self.delta[iLayer] = np.dot(self.W[iLayer].T, self.delta[iLayer+1]) * (self.A[iLayer]*(1-self.A[iLayer]))
                # calculate dW and dB 
                if iLayer==0:
                    self.dW[iLayer] += self.X[i][:, np.newaxis] * self.delta[iLayer][:, np.newaxis].T
                else:
                    self.dW[iLayer] += self.A[iLayer-1][:, np.newaxis] * self.delta[iLayer][:, np.newaxis].T
                self.dB[iLayer] += self.delta[iLayer] 
        # update
        for iLayer in range(self.nLayers-1):
            self.W[iLayer] -= (self.alpha/self.M)*self.dW[iLayer]
            self.B[iLayer] -= (self.alpha/self.M)*self.dB[iLayer]
        
    def PlainAutoEncoder(self):
        for i in range(self.steps):
            self.BackPropAlgorithm()
            print "step:%d" % i, "Jw=%f" % self.Jw

    def ValidateAutoEncoder(self):
        for i in range(self.M):
            print self.X[i]
            for iLayer in range(self.nLayers - 1):
                if iLayer==0: # input layer
                    self.Z[iLayer] = np.dot(self.X[i], self.W[iLayer])
                else:
                    self.Z[iLayer] = np.dot(self.A[iLayer-1], self.W[iLayer])
                self.A[iLayer] = self.sigmod(self.Z[iLayer] + self.B[iLayer])
                print "\t layer=%d" % iLayer, self.A[iLayer]        

data=[]
index=[]
f=open('./data_matrix.txt','r')
for line in f.readlines():
    ss=line.replace('\n','').split('\t')
    index.append(ss[0])
    ss1=ss[1].split(' ')
    tmp=[]
    for i in xrange(len(ss1)):
        tmp.append(float(ss1[i]))
    data.append(tmp)
f.close()

x = np.array(data)
#print x
#归一化处理
xx = preprocessing.scale(x)
nNodes = np.array([ 10, 5, 10])
ae3 = AutoEncoder(xx,xx,nNodes)
ae3.PlainAutoEncoder()
ae3.ValidateAutoEncoder()

详细代码可以参见我的github