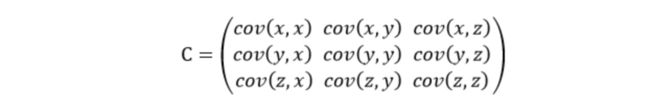深度学习入门之数学基础概念

深度学习之线代复习

标量、向量、矩阵和张量

• 标量（scalar）：一个标量就是一个单独的数。
• 向量：一个向量是一列数，这些数是有序排列的。我们可以把向量看作空间中的点，每个元素是不同坐标轴上的坐标。
• 矩阵：矩阵是一个二维数组，其中的每一个元素被两个索引（而非 一个）所确定。
• 张量（tensor）：在某些情况下，我们会讨论坐标超过两维的数组。一般地，一 个数组中的元素分布在若干维坐标的规则网格中，我们称之为张量。

矩阵的向量相乘

在深度学习中， 我们也使用一些不那么常规的符号。我们允许矩阵和向量相 加，产生另一个矩阵：C = A + b，其中 $C_{i,j}$ = $A_{i,j}$ + $b_j$。换言之，向量 b 和矩阵 A 的每一行相加。这个简写方法使我们无需在加法操作前定义一个将向量 b 复制 到每一行而生成的矩阵。这种隐式地复制向量 b 到很多位置的方式,被称为广播。

A ⊙ B（dot product）被称为元素对应乘积（element-wise product）或者Hadamard乘积（Hadamard product）

矩阵乘积满足分配律，结合率，但不一定满足AB=BA的交换律。

单位矩阵和逆矩阵

任意 向量和单位矩阵相乘，都不会改变。我们将保持 n 维向量不变的单位矩阵记作$I_n$ 。 形式上，$I_n$ ∈ $R^{n\times n}$ ， ∀x ∈ $R^n$ , $I_{n}x=x$.

矩阵 A 的矩阵逆（matrix inversion）记作 $A^{-1}$ ，其定义的矩阵满足如下条件$A^{-1}A=I_n$ .

线性相关和生成子空间

形式上，一组向量的线性组合，是指每个向量乘以对应标量系数之后的和，即：$\sum _i{c}_i{v}^{(i)}$

一组向量的生成子空间（span）是原始向量线性组合后所能抵达的点的集合。

如果一组向量中的任意一个向量都不能表示成其他向量的线性组合， 那么这组向量称为线性无关.

假设有一个$R^{2X2}$中的矩阵，它的两个列向量是相同的。那么它的列空间和它的一个列向量作为矩阵的列空间是一样的。也就是说，虽然矩阵有2列，但是它的列空间仍然只是一条线，不能涵盖整个$R^2$空间。也就是说这个列向量是冗余的。那么这种冗余称为线性相关。

如果一个矩阵的列空间涵盖整个 $R^m$ ，那么该矩阵必须包含至少一组 m 个线性无关的向量。这是式Ax=b对于每一个向量b的取值都有解的充分必要条件。

一个列向量线性相关的方阵被称为奇异的（singular）。

范数

形式上，$L^p$ 范数定义：$||x|{|}_p={(\sum _i|x{|}^p)}^{\frac{1}{p}}$其中 p ∈ R，p ≥ 1。

当 p = 2 时，$L^2$范数被称为 欧几里得范数（Euclidean norm）。它表示从原点出发到向量 x 确定的点的欧几里得距离。

Frobenius范数：$||A|{|}_F=\sqrt{\sum _{i,j}{A}_{i,j}^2}$

特殊类型的矩阵和向量

对角矩阵（diagonal matrix）只在主对角线上含有非零元素，其他位置都是零。对角矩阵受到关注的部分原因是对角矩阵的乘法计算很高效。

对称矩阵（symmetric matrix）是转置和自己相等的矩阵：$A=A^T$

正交矩阵（orthogonal matrix）是指行向量和列向量是分别标准正交的方针：$ A^TA=AAT=I$ 这意味着$A^{-1}=A^T$ 所以正交矩阵受到关注是因为求逆计算代价小。

特征分解

方针A的特征向量是指与A相乘后相当于对该向量进行缩放的非零向量v：$Av=\lambda v$ 标量$\lambda$被称为这个特征向量对应的特征值。

利用特征分解去分析矩阵A时，得到特征向量构成的矩阵V和特征值构成的$\lambda$，我们可以将A写作：$A=Vdiag(\lambda )V^{-1}$

我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了，而对角阵Σ里面的特征值是由大到小排列的，特征值对应的特征向量就是描述矩阵的变化方向。
当矩阵是高纬度的时候，矩阵就是高纬度空间下的线性变换，通过特征值分解得到的前N个向量就是矩阵最主要的N个变化的方向。利用这N个方向的变化来近似这个矩阵。也就是：提取这个矩阵最重要的一部分特征。（而特征值分解的局限就是变换的矩阵必须为方阵）

所有特征值都是正数的矩阵被称为正定（positive definite）；所有特征值都是非 负数的矩阵被称为半正定（positive semidefinite）。同样地，所有特征值都是负数的矩阵被称为负定（negative definite）；所有特征值都是非正数的矩阵被称为半负定 （negative semidefinite）。半正定矩阵受到关注是因为它们保证 ∀x, $x^{\top }Ax\ge 0$。此外， 正定矩阵还保证 $x^{\top }Ax=0$ $\Rightarrow$ $x=0$。

奇异值分解

还有一种分解矩阵的方法称为奇异值分解（SVD），将矩阵分解为奇异向量和奇异值。但是相对于特征分解，奇异值分解具有更广泛的应用。每一个实数矩阵都有一个奇异值分解，但不一定都有特征分解。例如，非方阵的矩阵没有特征分解，这时我们只能使用奇异值分解。

奇异值分解将矩阵分解成三个矩阵的乘积：

$$A=UD{V}^T$$

上述式子表示：矩阵A的作用就是将一个向量从V这组正交基向量的空间旋转到U这组正交基组成的空间，并且按照D在各个方向做了缩放，缩放的倍数就是奇异值。

假设 A 是一个 m × n 的矩阵，那么 U 是一个 m × m 的矩阵，D 是一个 m × n 的矩阵，V 是一个 n × n 矩阵。矩阵U和V都定义为正交矩阵，而矩阵D定义为对角矩阵。注意，矩阵D不一定是方阵。

对角矩阵 D 对角线上的元素被称为矩阵 A 的 奇异值（singular value）。矩阵 U 的列向量被称为 左奇异向量（left singular vector），矩阵 V 的列向量被称 右奇异 向量（right singular vector）。

A 的 左奇异向量（left singular vector）是 $A{A}^{\top }$ 的特征向量。A 的 右奇异向量（right singular vector）是 $A^{\top }A$ 的特征向量。A 的非零奇异值是 $A^{\top }A$ 特征值的平方根，同时也是 $A{A}^{\top }$ 特征值的平方根。

SVD 最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。

伪逆

但是计算伪逆的实际算法没有基于这个定义，而是使用下面的公式：

$A^{+}=V{D}^{+}{U}^T$

其中， 矩阵 U，D 和 V 是矩阵 A奇异值分解后得到的矩阵。对角矩阵 D 的伪逆 D + 是其非零元素取倒数之后再转置得到的。

迹运算

迹运算返回的是矩阵对角元素的和：$Tr(A)=\sum A_{i,i}$

迹运算提供了另一种描述矩阵Frobenius范数的方式：$||A|{|}_F=\sqrt{Tr(A{A}^T)}$

多个矩阵相乘得到的方阵的迹，和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的。当然，我们需要考虑挪动之后矩阵的乘积依然定义良好：Tr(ABC) = Tr(CAB) = Tr(BCA).

即使循环置换后矩阵乘积得到的矩阵形状变了，迹运算的结果依然不变。假设矩阵A∈$R^{m\ast n}$,矩阵B∈$R^{n\ast m}$，我们可以得到$Tr(AB)=Tr(BA)$

标量在迹运算后仍然是它自己：a = Tr(a)

概率与信息论

概率分布

概率分布用来描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小。我们描述概率分布的方式取决于随机变量是离散的还是连续的。

离散型变量和概率质量函数

离散型变量的概率分布可以用 概率质量函数（probability mass function, PMF）来描述。我们通常用大写字母 P 来表示概率质量函数。

如果一个函数 P 是随机变量 x 的 PMF，必须满足下面这几个条件：

• P 的定义域必须是 x 所有可能状态的集合。

• ∀x ∈ x, 0 ≤ P(x) ≤ 1. 不可能发生的事件概率为 0，并且不存在比这概率更低的状态。类似的，能够确保一定发生的事件概率为 1，而且不存在比这概率更高的状态。

• ${\sum }_{x\in x}P(x)=1$. 我们把这条性质称之为归一化的（normalized）。如果没有这条性质， 当我们计算很多事件其中之一发生的概率时可能会得到大于 1 的概率。

连续型变量和概率密度函数

当我们研究的对象是连续型随机变量时， 我们用概率密度函数（probability density function, PDF）而不是概率质量函数来描述它的概率分布。如果一个函数 p 是概率密度函数，必须满足下面这几个条件：

• p 的定义域必须是 x 所有可能状态的集合。
• ∀x ∈ x, p(x) ≥ 0. 注意，我们并不要求 p(x) ≤ 1。
• $\int p(x)dx=1$

###边缘概率

我们知道了一组变量的联合概率分布，但想要了解其中一个子集的概率分布。这种定义在子集上的概率分布被称为边缘概率分布（marginal probability distribution）。

例如，假设有离散型随机变量 x 和 y，并且我们知道 P(x, y)。我们可以依据下面的求和法则（sum rule）来计算 P(x)：$\forall x\in x,P(x=x)=\sum _{y}P(x=x,y=y)$

对于连续型变量，我们需要用积分替代求和：$p(x)=\int p(x,y)dy$

条件概率

我们将给定 x = x，y = y 发生的条件概率记为 P(y = y | x = x)。这个条件概率可以通过下面的公式计算：$p(y=y|x=x)=\frac{p(y=y,x=x)}{p(x=x)}$

条件概率的链式法则

$P(x^{(1)},...,x^{(n)})=P(x^{(1)}{\prod }_{i=2}^{n}P(x^{(i)}|x^{(1)},...,x^{(i-1)})$.

独立性和条件独立性

两个随机变量 x 和 y，如果它们的概率分布可以表示成两个因子的乘积形式，并 且一个因子只包含 x 另一个因子只包含 y，我们就称这两个随机变量是 相互独立的 （independent）：

∀x ∈ x, y ∈ y, p(x = x, y = y) = p(x = x)p(y = y).

如果关于 x 和 y 的条件概率分布对于 z 的每一个值都可以写成乘积的形式， 那么这两个随机变量 x 和 y 在给定随机变量 z 时是 条件独立的（conditionally independent）：

∀x ∈ x, y ∈ y, z ∈ z, p(x = x, y = y | z = z) = p(x = x | z = z)p(y = y | z = z).

x⊥y 表示 x 和 y 相互 独立，x⊥y | z 表示 x 和 y 在给定 z 时条件独立。

期望、方差和协方差

####期望

设P(x)是一个离散概率分布函数，自变量的取值范围为{x1,x2,⋯,xn}{x1,x2,⋯,xn}。其期望被定义为：$E(x)=\sum _{k=1}^n{x}_{k}p(x_k)$

设p(x)是一个连续概率密度函数。其期望为： $E(x)={\int }_{-\infty }^{+\infty }xp(x)dx$

期望是线性的，E(ax+by+c)=aE(x)+bE(y)+c。

方差

方差是一种特殊的期望，被定义为：$Var(x)=E((x-E(x){)}^2)$

方差（variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是各个数据分别与其平均数之差的平方的和的平均数。

标准差

方差的平方根被称为标准差。

协方差

两个随机变量的协方差被定义为： Cov(x,y)=E((x−E(x))(y−E(y)))

协方差的结果有什么意义呢？如果结果为正值，则说明两者是正相关的（从协方差可以引出“相关系数”的定义），也就是说一个人越猥琐越受女孩欢迎。如果结果为负值， 就说明两者是负相关，越猥琐女孩子越讨厌。如果为0，则两者之间没有关系，猥琐不猥琐和女孩子喜不喜欢之间没有关联，就是统计上说的“相互独立”。

协方差矩阵

前面提到的猥琐和受欢迎的问题是典型的二维问题，而协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算$C_n^2=\frac{n!}{2!\ast (n-2)!}$个协方差，那自然而然我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

这个定义还是很容易理解的，我们可以举一个三维的例子，假设数据集有三个维度，则协方差矩阵为：

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度的方差。

常用概率分布

1.Bernoulli 分布（Bernoulli distribution）是单个二值随机变量的分布。它由单个参数 ϕ ∈ [0, 1] 控制，ϕ 给出了随机变量等于 1 的概率。故其为离散型概率分布。

$P(x=1)=p$

$P(x=0)=1-p$

$P(x=x)=p^x(1-p{)}^{1-x}$

$E(x)=\sum _{k=1}^n{x}_{k}p(x_k)=1\ast p+0\ast (1-p)=p$

$Var(x)=E((x-E(x){)}^2)=(1-p{)}^2\ast p+(0-p{)}^2\ast (1-p)=p\ast (1-p)$

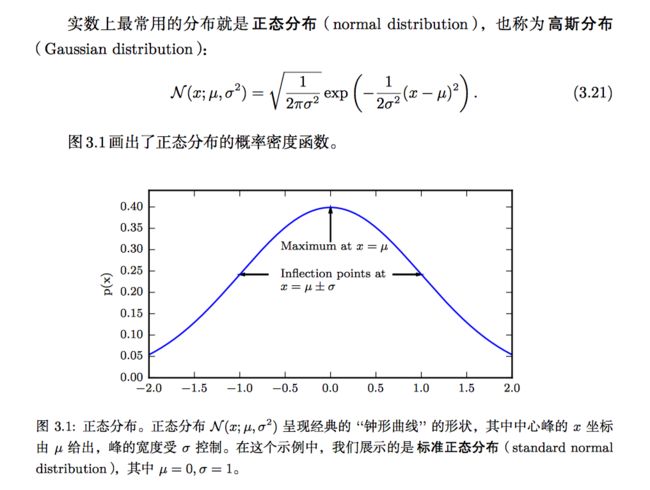
4.高斯分布

5.指数分布

指数分布有如下的适用条件：

1. x是两个事件发生之间的时间间隔，并且x>0;
2. 事件之间是相互独立的；
3. 事件发生的频率是稳定的；
4. 两个事件不能发生在同一瞬间。

指数分布的概率密度函数（probability density func,PDF）由λ和x(时间)构成：

$f(x)=\lambda e^{-\lambda x}$

其中λ是事件发生的频率。

6.Laplace分布

7.dirac分布

概率密度函数：$p(x)=\delta (x-\mu )$

Dirac delta 函数被定义成在除了 0 以外的所有点的值都为 0，但是积分为 1。通过把 p(x) 定义成 δ 函数左移 −µ 个单位，我们得到了一个在 x = µ 处具有 无限窄也无限高的峰值的概率质量。

贝叶斯规则

$P(x|y)=\frac{P(x)P(y|x)}{P(y)}$