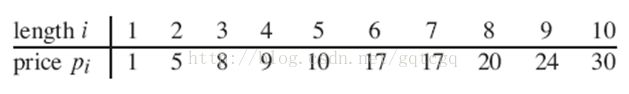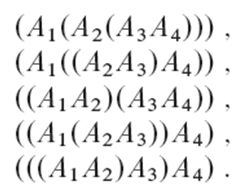算法导论 第15章 动态规划

《算法导论》这门课的老师是黄刘生和张曙，两位都是老人家了，代课很慢很没有激情，不过这一章非常有意思。更多见：iii.run

---

前言：

书中列举四个常见问题，分析如何采用动态规划方法进行解决。
　　装配线调度问题
　　矩阵链乘问题：
　　最长公共子序列问题：
　　最优二叉查找树问题：

基本概念

动态规划通常应用于最优化问题，此类问题可能包含多个可行解。每个解有一个值，而我们期望找到最大或者最小的解。

动态规划算法的设计可以分为以下4个步骤：

• 描述最优解的结构。
• 递归定义最优解的值。
• 按自底向上的方式计算最优解的值。（其实还应该有自顶向下的求解）
• 由计算出的结果构造一个最优解。

动态规划算法效率会非常高的原因在于，其特殊的实现方法，也就是第三步。

两种等价的实现方法：

• 带备忘的自顶向下法，此方法按照正常的递归编写过程，但过程会保存每个子问题的解（通常保存在一个数组或散列表中）。当需要一个子问题的解时，程序首先检查是否已经保存过此解。如果是，直接返回；若不是，递归计算这个子问题。这种递归方式是带备忘的。
• 自底而上法，这种方法需要恰当的定义子问题的规模，因为任何一个子问题的求解的依赖着更小的子问题。因此需要将问题进行排序，从小的问题开始处理。这样可以确保，在处理到大的问题时，其所依赖的更小的子问题已经求解完毕，结果已经保存。

因此，我们会说 动态规划算法属于典型的用空间换取时间。由于没有频繁的递归函数的开销，自底而上方法的时间复杂度会更好一些。

动态规划与分治法之间的区别：

• 分治法是指将问题分成一些独立的子问题，递归的求解各子问题。
• 动态规划适用于这些子问题不是独立的情况，也就是各子问题包含公共子问题。

动态规划基础

什么时候可以使用动态规范方法解决问题呢？这个问题需要讨论一下，书中给出了采用动态规范方法的最优化问题中的两个要素：最优子结构和重叠子结构。

最优子结构（自下向上）

最优子结构是指问题的一个最优解中包含了其子问题的最优解。在动态规划中，每次采用子问题的最优解来构造问题的一个最优解。

寻找最优子结构，遵循的共同的模式：

• 问题的一个解可以是做一个选择，得到一个或者多个有待解决的子问题。

• 假设对一个给定的问题，已知的是一个可以导致最优解的选择，不必关心如何确定这个选择。

• 在已知这个选择后，要确定哪些子问题会随之发生，如何最好地描述所得到的子问题空间。

• 利用“剪贴”技术，来证明问题的一个最优解中，使用的子问题的解本身也是最优的。

最优子结构在问题域中以两种方式变化：

• 有多少个子问题被使用在原问题的一个最优解中。
• 在决定一个最优解中使用哪些子问题时有多少个选择。

动态规划按照自底向上的策略利用最优子结构，即：首先找到子问题的最优解，解决子问题，然后逐步向上找到问题的一个最优解。

为了描述子问题空间，可以遵循这样一条有效的经验规则，就是尽量保持这个空间简单，然后在需要时再扩充它。

注意：在不能应用最优子结构的时候，就一定不能假设它能够应用。 警惕使用动态规划去解决缺乏最优子结构的问题！

重叠子问题（自上向下）

用来解决原问题的递归算法可以反复地解同样的子问题，而不是总是产生新的子问题。

重叠子问题是指当一个递归算法不断地调用同一个问题。

动态规划算法总是充分利用重叠子问题，通过每个子问题只解一次，把解保存在一个需要时就可以查看的表中，每次查表的时间为常数。

由计算出的结果反向构造一个最优解：把动态规划或者是递归过程中作出的每一次选择（记住：保存的是每次作出的选择）都保存下来，在最后就一定可以通过这些保存的选择来反向构造出最优解。

做备忘录的递归方法：这种方法是动态规划的一个变形，它本质上与动态规划是一样的，但是比动态规划更好理解！
　　（1） 使用普通的递归结构，自上而下的解决问题。
　　（2） 当在递归算法的执行中每一次遇到一个子问题时，就计算它的解并填入一个表中。以后每次遇到该子问题时，只要查看并返回表中先前填入的值即可。

钢条切割问题

题目

给定一个长度为n的钢条，以及一个价格表p，p中列出了每英寸钢条的价格，将长度为n的钢条切割为若干短钢条出售，求一个钢条的切割方案，使得收益最大，切割工序没有成本。比如价格表p如下：

长度为n的钢条，一共有$2^{n-1}$种不同的切割方案，因为可以再距离钢条左边为i（i=1,2,…,n-1）处，我们总是可以选择切割或者不切割。比如下图表示了n=4的切割情况：

mark

理论依据

我们称钢条切割问题满足最优子结构性质：问题的最优解由相关子问题的最优解组合而成，而这些子问题可以独立求解。

我们可以这样理解钢条问题：将钢条从左边切下一段长度为i的一段，对剩下的n-i的部分继续进行切割（递归求解），而不对左边长度为i的一段在进行切割。

$r_n = \mathop{max}\limits_{1 \leq i \leq n} (p_i + r_{n-i})$

这样问题的解就转化为最优解了。

自顶向下递归实现

CUT-ROD(p,n)
if  n == 0
    return  0
q = -∞
for  i = 1 to n
   q = max(q,  p[i]+CUT-ROD(p, n-i))
return  q

CUT-ROD的效率很差，这是因为CUT-ROD反复的求解一些相同的子问题，下图显示了当n==4时的调用情况：

mark

带备忘的自顶向下

MEMOIZED-CUT-ROD(p,n)
let  r[0..n] be a new array
for  i = 0 to n
    r[i]= -∞
return  MEMOIZED-CUT-ROD-AUX(p, n, r)
 
MEMOIZED-CUT-ROD-AUX(p,n, r)
if  r[n] >= 0
    return  r[n]
if  n == 0
    q = 0
else  q = -∞
    for  i = 1 to n
        q= max(q,  p[i]+MEMOIZED-CUT-ROD-AUX(p, n-i,r))
r[n] = q
return q

该方法与之前的普通递归方法类似，只是会在过程中保存子问题的解，当需要一个子问题的解的时候，先查看是否已经保存过了，如果是，则直接使用即可。否则，按常规的递归方式计算子问题。所以称为带备忘的，因为它记住了之前已经计算出的结果。

自底向上的方法

BOTTOM-UP-CUT-ROD(p,n)
let  r[0..n] be a new array
r[0]= 0
for  j = 1 to n
    q= -∞
    for  i = 1 to j
        q = max(q, p[i]+r[j-i])
    r[j]= q
return  r[n]

方法采用子问题的自然顺序，因此过程中依次求解规模为$j=0,1,2,3,4...,n$的问题。

这两种算法具有相同的时间复杂度，BOTTOM-UP-CUT-ROD主要是双层嵌套循环，所以时间复杂度$Θ(n^{2)$。MEMOIZED-CUT-ROD的时间复杂度也是$Θ(n}2)$。可以使用子问题图进行分析。

python实现切割钢条问题

def cut_rod():
    p = [0,1,5,8,9,10,17,17,20,24,30]
    n = len(p)
    r = [0 for i in range(n)]
    s = [0 for i in range(n)]
    for j in range(n):
        q = -10
        for i in range(j+1):
            if q < (p[i]+r[j-i]):
                q = (p[i]+r[j-i])
                s[j] = i
            #q = max(q,p[i]+r[j-i])
        r[j] = q
        
def find_way(n):
    cut_rod()
    print(n,'--->',r[n])
    while n > 0:
        print(s[n])
        n = n - s[n]

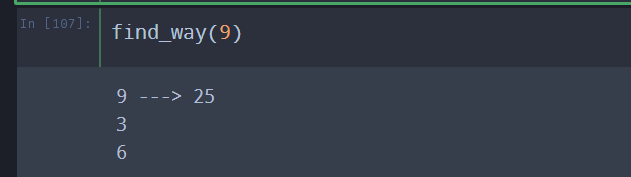
调用find_way(9)输出

矩阵链乘法

题目

给定n 个矩阵的序列，希望求它们的乘积：$A_1A_2A_3...A_n$ 。因为矩阵的乘法满足结合律，所以可以对n个矩阵序列加括号，来改变乘积顺序。比如对于矩阵链< $A_1$, $A_2$,$A_3$,$A_4$>可以有下面的加括号方案：

不同的加括号的方案，对于乘积运算的代价影响很大.

两个矩阵相乘，A为p * q矩阵，B为q * r矩阵。所以A 的乘法次数为pqr。

如果A（10,100 ），B（100,5）， C（5,50 ）三个矩阵相乘。

如果按照((AB)C)的顺序，则需要101005 + 10550 = 7500次乘法运算，如果按照(A(BC))的顺序，则需要100550 + 1010050 = 75000次乘法运算。所以，不同的加括号方案，对于矩阵链乘法的代价影响很大。

解题步骤

刻画最优解的结构特征

通过寻找最优子结构，利用最优子结构从子问题的最优解中构造出原问题的最优解。
假设$A_iA_{i+1}...A_j$的最优括号花方案的分割点是在$A_k$和$A_{K+1}$之间，一个非平凡的矩阵链乘法任何时候都是需要划分链的，任何最优解都是有子问题的最优解构成的。

递归的定义最优解的值

令$m[i,j]$表示计算矩阵$A_{i,j}$所需标量乘法的最小值，也即原问题的最优解，计算$A_{1..n}$的最低代价就是$m[1,n]$。

• 对于i == j 的平凡问题，矩阵链只包含唯一的矩阵$A_{i,j}$。
• 对于$A_iA_{i+1}...A_j$的最优括号化方案的切割点在$A_k$和$A_{k+1}$之间。那么$m[i,j]$的解相当于计算$A_{i..k}$和$A_{k+1..j}$的代价加上，合并这两个子答案所需要的代价$p_{i-1}p_k p_j$

因此，我们得到

$$m[i,j] = m[i,k]+m[k,j]+p_{i-1}p_k p_j$$

计算最优解的值

算法应当按照长度递增的顺序求解矩阵链括号化问题，并按照对应的顺序填写表m。对举证连$A_{i,j}$，其规模为链的长度j-i+1

伪代码就不写了，直接写python代码

python实现矩阵链乘法问题

def MATRIX_CHAIN_ORDER(p):  
    n = len(p)  
    s = [[0 for j in range(n)] for i in range(n)]  
    m = [[0 for j in range(n)] for i in range(n)]  
    for l in range(2, n):           #l is the chain length  
        for i in range(1, n-l+1):  
            j = i + l - 1  
            m[i][j] = 1e9  
            for k in range(i, j):  
                q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]  
                if q < m[i][j]:  
                    m[i][j] = q  
                    s[i][j] = k  
    PRINT_OPTIMAL_PARENS(s, 1, n-1)
    return m
    
      
def PRINT_OPTIMAL_PARENS(s, i, j):  
    if i == j:  
        print('A', end = '')  
        print(i, end = '')  
    else:  
        print('(', end = '')  
        PRINT_OPTIMAL_PARENS(s, i, s[i][j])  
        PRINT_OPTIMAL_PARENS(s, s[i][j]+1, j)  
        print(')', end = '')  
   

if __name__ == "__main__":
    A = [30, 35, 15, 5, 10, 20,25]
    m = MATRIX_CHAIN_ORDER(A) 
    print('\n','共计需要',m[1][n-1],'次相乘')

---

以上