树链剖分

自从漫长暑假的两次培训由于某些原因就再没整理过博客

仔细分析一下qbxt的教学模式已经内容,无非就是讲知识点,讲题目罢了,而且为了赶进度,速度也非常快

那么把qbxt整理博客拆分成若干的知识整理博客以及题目整理博客,而非以往的单纯罗列知识点的,对于那些难题写一写口胡思路但是对其算法没有进行实现,甚至不了解该算法的"八股博客"(我只是在说我自己的),两者相比学习效果要差太多了

所以以后的博客整理将侧重知识点的梳理,而非罗列我本身也尽量避免"八股"的出现,

做到言之有物,整之有理,观之有效

我尽量8

好,废话不再说一些(临沂口音)

树剖

前置芝士:

树的基本操作(邻接表,树上dfs啥的),

基本的线段树(要求充分理解并熟练掌握),

LCA基本思路(理解为什么要选尽量深的节点跳)

后两个不懂的我博客都有哈!

一些问题:

树剖是啥?

废话,树链剖分树剖就是通过某种算法对树上信息进行整理,使树上的查询更加方便的算法

树剖的具体目的?

主体思路是将树拆分成有着某种特定性质的区间,使得这个(或这些)区间可以利用数据结构进行处理,以实现用数据结构进行树上信息维护和查询

怎么实现?

急嘛?这篇博客就是要讲这个啊?!

---

正文:

下面来讲理论以及实现方式

首先入门需要知道这样几个变量:

第一组:

int fa[N],son[N],dep[N],size[N];

fa[]的意义很明确,就是该节点的父亲

而size[]指的就是以当前节点为根的子树的大小

dep[]是该节点的深度

这个son[]指的是"重儿子",并不是用来储存点的所有儿子

重儿子指的是对于一个节点,其儿子中以该儿子为根的子树最大的一个儿子

说人话就是size[]最大的儿子

说到这个就应该想到怎么维护了吧...

这里的一组变量目的就在于维护每个点的基本信息,并且把这个叫做"重儿子"的东西处理出来

这个重儿子有什么用呢?

我们先回到树剖根本目的上去,要把树拆成区间,把树拆成一条一条的链

我们只需要保证这些链上的点所使用的下标是连续的,就可以在使用数据结构的时候对应的查询这些链所对应的区间

那么我们规定这些重儿子组成的链就是链,特殊的,对于作为非重儿子(下简称为轻儿子)的叶节点,自成一链

当然这个东西别人叫做重链,

关于为什么要用重儿子组成链...

记住就好了,这就是一条准则

那不是重儿子的节点怎么办呢?

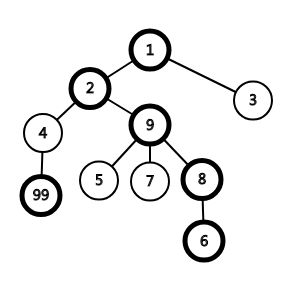
我们看下下面这棵树:

这个黑框的点就是上一个点的重儿子(1没有父亲不算),那么显然这个图中的链是这样的:

{1,2,9,8,6}; {4,9}; {5}; {7}; {3};

我们可以看出,非叶节点轻儿子总是一条链的头,就是"链首",包括1也是这样,因为它是个孤儿(滑稽

这样一来,我们可以将每个点归为一条链中的元素,从而实现树的区间化

这个"链"就是别人所说的叫做"重链"的东西,然而因为所有点其实都属于某一条链,所以其实"链"并没有种类区分,暂且统一记作"链"

总结一下

这组变量是用来处理点的基本信息的,为正式树链剖分打基础

就是预处理,用dfs实现

变量的应用---代码实现

inline void dfs1(ci u,ci f,ci depth){
    dep[u]=depth;
    fa[u]=f;
    size[u]=1;
    int maxn=-1;
    for(int i=head[u];i;i=ed[i].nxt){
        int v=ed[i].to;
        if(v==f)continue;
        dfs1(v,u,depth+1);
        size[u]+=size[v];
        if(size[v]>maxn)son[u]=v,maxn=size[v];
    }
}

觉得还比较好理解

第二组:

处理完基本信息就要进行树剖了

需要变量如下:

int dfn[N],top[N],a[N],num[N],cnt=0;

我们通过dfn[] (dfs序)和cnt来对每个点进行重新编号,确定每个点的新下标,作为接下来搭配数据结构的下标,原因如下:

我们知道dfs使得一条连续路径(就是一直搜下去的路径,没有递归)的dfn是连续的,

那么如果使得同一条链上所有的dfn连续,那么就可以搭配数据结构进行链的查询,从而实现路径的查询

如何使得链上元素连续呢?

第一次dfs已经处理出了一个叫重儿子的东西,那么只要每次深搜时优先选择搜索重儿子,那么可以使得由重儿子组成的链的dfn是连续的

这样一来,这个树就由若干个具有连续dfn的链所构成

那么迄今为止,dfn序有着以下性质:

1.对于同一条链,其dfn连续

2.对于同一条链,深度小的点dfn更小

而top[]就是每个链中dfn(或者说深度)最小的那个

a[]是需要搭配的数据结构的元素,一般就是线段树吧...

num[]是一开始题目给的每一个点的点权

这两个变量不放到实际题目中没有实际意义

cnt就是dfn的一个累计

代码如下:

inline void dfs2(ci u,ci boss){
    dfn[u]=++cnt;
    a[cnt]=num[u];  //这句是用来搭配数据结构的
    top[u]=boss;
    if(!son[u]) return ;
    dfs2(son[u],boss);
    for(int i=head[u];i;i=ed[i].nxt){
        int v=ed[i].to;
        if(son[u]!=v&&fa[u]!=v)
        dfs2(v,v);
    }
}

总体思路在于每次在搜索的时候先处理当前节点的dfn和top(那个boss是用来传top的,因为同一重链的top一样),

然后判断有没有重儿子,如果没有就说明它连儿子都没有,没有继续dfs的必要,直接结束函数

否则先搜重儿子,保证重儿子组成的链连续,因为搜索序连续

搜完以后再搜非重儿子的其他儿子

刚刚已经说了非重儿子一定是top了...

现在我们又可推知dfn的一个性质:

对于同一子树,其中节点的dfn一定是连续的,就是假设根节点的dfn为i,那么子树中最大的dfn只能是i+size[那个节点]-1

好证,因为对于一棵树的搜索是连续的,不可能搜了这棵树的一部分再去搜别的树,然后再回来搜这棵树

至此,预处理完毕,树链剖分也基本接近尾声

现在所要的只是搭配数据结构的修改和查询

搭配的方法就是将新的下标dfn做为序列的下标,用树状数组,线段树进行信息维护

主要用线段树,对于那些需要对数据进行特殊处理的需要把线段树的区间合并法则啥的改一下

对于路径修改与查询,先要了解一个东西:

树剖求LCA,

(以下所有什么"亲缘关系","祖先关系"都是指一个点是另一个点祖先)

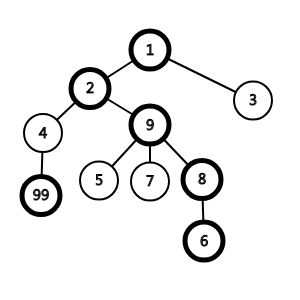
现在再拿出这张图来:

现在要求查询99节点到6号节点的LCA,现在看一下它们所属的链:

{4,99}

{1,2,9,8,6}

它们并不在同一条链,说明他们之中并不存在祖先关系,并不能一下找出LCA

那么我们选择top深度比较大的往上跳,跳到这个点的top的父亲,再看是不是属于同一条链,不是的话继续按照这个法则跳,如果属于同一条链,就直接返回上面的点,

注意这里是判断是否是同一条链而非路径,就是说就算其中存在亲缘关系,也不能直接判断,就像是上面那张图的4和2,他们的LCA显然是2,然而因为他们不属于同一条链,程序并无法识别这是LCA,只好按规则老实跳了...

显然选择top深度小的会无限往上跳,因为如果两个点不属于一条链,跳top深度小的也不会改变这一状况

我们按照这个法则用上面那个图模拟下:

1.99号节点的top(4号节点)深度较小,将它跳到这个top的父亲(2号节点)上,判断现在两点处于同一条链,跳出循环

2.返回深度小的2号节点,作为LCA

这个是树剖求LCA的基本理论流程

代码:

inline void insert1(int x,int y,ci v){
    while(top[x]!=top[y]){
        if(dep[top[x]]dep[y])swap(x,y);
    return x;
}

进一步地,我们知道树上两点的最短路径是两个点分别到LCA的路径之和,

那么我们可以在查询LCA的同时将一直以来跳的路径信息记录下来,就可以实现路径查询

代码(用的搭配线段树query的查询):

inline int query1(int x,int y){
    int ans=0;
    while(top[x]!=top[y]){
        if(dep[top[x]]dep[y])swap(x,y);
    ans+=query(1,1,n,dfn[x],dfn[y]);
    return ans%p;
}

当然修改也可以,将函数啥的换一下就好了

对于子树操作,我们知道一颗子树内的dfn连续,

所以只要查询以dfn[根节点]为开始,长度为size[根节点]的序列，就完成了整个子树的查询

对于修改,也同理,把区间查询函数改成插入函数即可

代码:

inline int query2(int x){
    return query(1,1,n,dfn[x],dfn[x]+size[x]-1);
}

这就是树剖的基本预处理和修改查询

看下板子题:

树剖模板

就是以上所有操作,不用解释,上代码:

#include
#include
#include
using namespace std;
#define ci const int&
const int N=100005;
const int M=N;
int n,m,r,p;
int a[N];
int sum[N<<2];
int laz[N<<2];
inline void build(ci k,ci l,ci r){
    if(l==r){
        sum[k]=a[l]%p;
        return ;
    }int mid=l+r>>1;
    build(k<<1,l,mid);
    build(k<<1|1,mid+1,r);
    sum[k]=(sum[k<<1]%p+sum[k<<1|1]%p)%p;
}
inline void add(ci k,ci l,ci r,ci v){
    sum[k]=sum[k]+(r-l+1)*v%p;
    laz[k]=(laz[k]%p+v%p)%p;
}
inline void pushdown(ci k,ci l,ci r){
    if(!laz[k])return ;
    int mid=l+r>>1;
    add(k<<1,l,mid,laz[k]);
    add(k<<1|1,mid+1,r,laz[k]);
    laz[k]=0;
}
inline void insert(ci k,ci l,ci r,ci x,ci y,ci v){
    if(x<=l&&r<=y){
        add(k,l,r,v);
        return ;
    }int mid=l+r>>1;
    pushdown(k,l,r);
    if(x<=mid) insert(k<<1,l,mid,x,y,v);
    if(mid>1;
    int ret=0;
    if(x<=mid) ret=(ret+query(k<<1,l,mid,x,y))%p;
    if(midmaxn)son[u]=v,maxn=size[v];
    }
}
inline void dfs2(ci u,ci boss){
    dfn[u]=++cnt;
    a[cnt]=num[u];
    top[u]=boss;
    if(!son[u]) return ;
    dfs2(son[u],boss);
    for(int i=head[u];i;i=ed[i].nxt){
        int v=ed[i].to;
        if(son[u]!=v&&fa[u]!=v)
        dfs2(v,v);
    }
}
inline void insert1(int x,int y,ci v){
    while(top[x]!=top[y]){
        if(dep[top[x]]dep[y])swap(x,y);
    insert(1,1,n,dfn[x],dfn[y],v);
}
inline void insert2(ci x,ci v){
    insert(1,1,n,dfn[x],dfn[x]+size[x]-1,v);
}
inline int query1(int x,int y){
    int ans=0;
    while(top[x]!=top[y]){
        if(dep[top[x]]dep[y])swap(x,y);
    ans+=query(1,1,n,dfn[x],dfn[y]);
    return ans%p;
}
inline int query2(int x){
    return query(1,1,n,dfn[x],dfn[x]+size[x]-1);
}
int main(){
    scanf("%d%d%d%d",&n,&m,&r,&p);
    for(int i=1;i<=n;i++)
        scanf("%d",&num[i]);
    for(int i=1;i

然后对于其他题目,就只是修改线段树的问题辣!

贴几个题目:
Qtree1

Qtree3