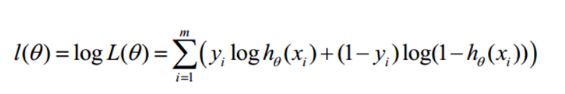1. RF, GBDT 的区别; GBDT,XGboost 的区别
GBDT在训练每棵树时候只能串行,不能并行,在确定分割节点和分割值的时候可以对多个特征进行并行
Random Forest可以并行
Bagging(RF):每次有放回的采样n个样本,采样K次形成K个数据集,训练每棵树时,采样一定数量特征进行训练,汇总在一起进行预测
Boosting: 提升的思想,串行训练一系列弱分类器,每个弱分类器的训练依赖于之前分类器训练的结果。
如:
Boosting Tree : 如GBDT, 每棵树(弱分类器)学习之前的残差,最后线性求和
Adaboost: 被错分次数多的样本会被加权,准确率高的弱分类器权重更大,最终加权求和/加权vote
Bagging和Boosting(这里拿Adaboost举例)的区别:
- 样本选择上:
Bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
Boosting:每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整 (这里指Adaboost,GBDT样本权重也不边)。- 样例权重:
Bagging:使用均匀取样,每个样例的权重相等。
Boosting:根据错误率不断调整样例的权值,错误率越大则权重越大。(这里指adaboost)- 预测函数:
Bagging:所有预测函数的权重相等。
Boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。- 并行计算:
Bagging:各个预测函数可以并行生成。
Boosting:各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果。
GBDT:
GBDT使用多棵CART树来做一个boosting的回归,每棵树学习上一轮结果的残差,原理是使用梯度下降,对上一棵树的损失函数求一阶导数,去拟合负一阶导数的值。
如下图的Gradient Boosting的算法图
第3步是计算每个样本在当前轮次的一阶导数
第4步是寻找最好拟合每个样本负一阶导数的树的新CART树。
第5步是搜索一个步长,最小化损失函数
第6步确定当前创建的新CART树的结果,具体为 学习率 * 步长 * 当前树的输出结果
第7步,boosting到新的函数上。
GBDT与xgboost的区别(个人理解):
xgboost是GBDT的一种优化过的实现。
在GBDT的基础上,加入了如下特性:
- 加入了树的模型复杂度的正则项,可以更好的优化结构风险。
- 在计算梯度时候,传统GBDT只用到了损失的一阶导数,xgboost在优化方法上不同于上面GBDT所使用的Gradient Boosting,而是也使用了二阶导,相当于使用了牛顿法。
- xgboost参考和加入了random forest的很多优点,比如行采样列采样,即采样80%的样本训练下一颗提升树,采样80%的特征训练等。
- boosting在方差-偏差分解中是降低了偏差,bagging(random forest)是降低了方差,因为RF用了不同的子模型,而xgboost增加了正则项,也一定程度的降低了方差,因此效果更好
不同于普通GBDT的heuristic式的学习(如使用Gini指数),xgboost明确定义的目标函数,由损失函数误差和正则项组成(经验风险和结构风险),在学习时候使用了泰勒展开式对经验风险做二阶导数的近似,因此在求每次的最小值时有一个明确的解析解。
xgb的slides中文: http://www.52cs.org/?p=429
chen tianqi的slides: https://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf
2. 决策树处理连续值的方法
1.对特征的取值进行升序排序
2.两个特征取值之间的中点作为可能的分裂点,将数据集分成两部分,计算每个可能的分裂点的信息增益(InforGain)。优化算法就是只计算分类属性发生改变的那些特征取值。
3.选择修正后信息增益(InforGain)最大的分裂点作为该特征的最佳分裂点
4.计算最佳分裂点的信息增益率(Gain Ratio)作为特征的Gain Ratio。注意,此处需对最佳分裂点的信息增益进行修正:减去log2(N-1)/|D|(N是连续特征的取值个数,D是训练数据数目,此修正的原因在于:当离散属性和连续属性并存时,C4.5算法倾向于选择连续特征做最佳树分裂点)
具体的做法与CART树选择分割点的值(value)是类似的,即先对所有样本在这个特征上的取值做排序,之后每次取两个特征值的中点作为分割点,之后计算最大收益(这里使用InfoGain信息增益)。
而CART树,是取中间点当做为个点后,计算样本左右分割之后的RMSE值(因为是回归问题)
3. 特征选择的方法
常用的方法论有SVD降维,PCA主成分分析等,L1正则。
工业界中常用的方法:
xgboost中自带的feature importance,包含了weight,gain等判别标准,get_fscore()方法
weight该特征在CART树中出现了多少次
gain该特征在CART树中获得信息增益的大小
可以使用该特征重要性判断新加入的特征是否显著,是否重要。
另一种可行的方法:
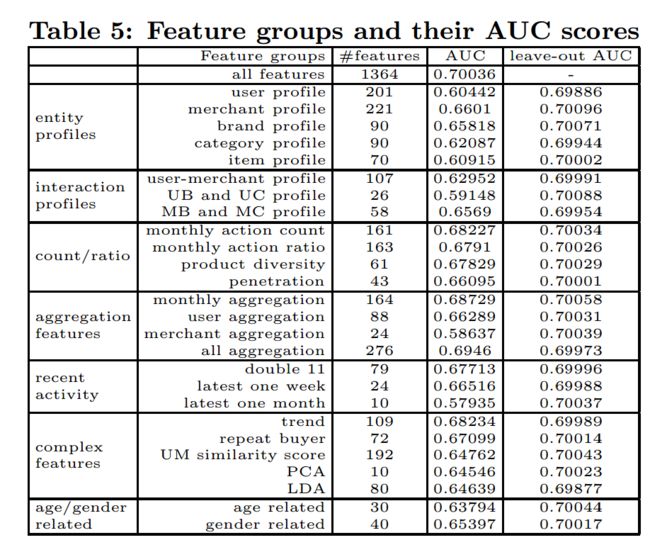
结合evaluation metric,比如对于二分类问题,判断单特征AUC,增加了某特征后的AUC变化,drop掉某特征后的AUC等几种方法。可参考文章Repeat Buyer Prediction for E-commerce http://www.kdd.org/kdd2016/papers/files/adf0160-liuA.pdf 里对特征有详细评估,AUC/leave-out AUC
4. 过拟合的解决方法
- 降低模型复杂度,改参数如GBDT减少树的深度、树的数量等,加正则如加入L2正则
- 很多具体模型方法,比如xgboost和random forest,每棵树对样本进行采样,对特征进行采样;神经网络中加入drop out等
- Early Stopping,模型训练时如果在evaluation集合指标如AUC,n轮没有下降,则停止模型的迭代
5. kmeans 的原理,优缺点以及改进
- 随机选取K个点当cluster中心
- 根据距离计算每个点所属cluster
- 重新计算每个cluster的中心
- 循环 2,3步,直到cluster不变或cluster的中心不变。
Kmeans能保证收敛,通常收敛到局部最优,可以多跑几次计算一下每个簇的误差距离之和,选择最小的那次。
Kmeans的缺点总结为下:
(1)对于离群点和孤立点敏感;
(2)k值选择;
(3)初始聚类中心的选择;
(4)只能发现球状簇。
6. 假设面试官什么都不懂,详细解释 CNN 的原理;
相当于一个模式匹配过程,每一个CNN的卷积核扫过图片的所有区域,来匹配某个区域是否有卷积所表示的形状特征,如圆形,弧线(卷积核的形状也是学习而得),最后将多个卷积核(多种模式)的匹配结果当做特征,来训练分类模型
7. 海量的 item 算文本相似度的优化方法;
simhash, LSH
8. 解释 word2vec 的原理以及哈夫曼树的改进;
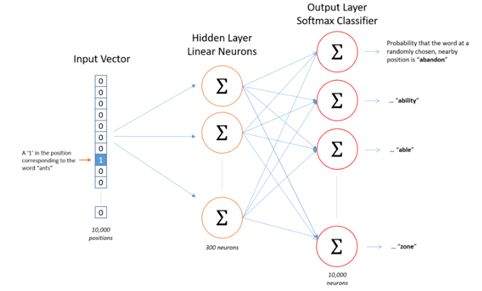
word2vec的模型分为CBOW和skip-gram,CBOW是用上下文一起预测中心词,skip-gram是中心词去预测上下文每个词。
在具体优化上,拿skip-gram举例,模型的输入是中心词的词向量,输出是上下文中的一个词,输出结果为one-hot 编码的话,模型相当于做一个多分类(比如有1000个词,预测词的可能性有1000种,就是做一个1000分类),使用一个softmax分类器,但softmax的优化很慢,相当于softmax参数矩阵的每一行上的参数都要更新。因此word2vec应用了两种softmax加速方法,第一种是基于霍夫曼树的层次softmax,第二种是基于负采样negative sampling的优化。
另外word2vec不仅要优化softmax的参数,同时也要优化词向量,
层次softmax相当于使用预料中的词频排序预先创建一颗霍夫曼树,词频越大的离根节点越近,也就是霍夫曼编码越短。霍夫曼树的输入是中心词的词向量(skip-gram),之后在霍夫曼树的每一个非叶子节点,做一个LR的二分类,也就是判断是否属于该非叶子节点的左叶子节点(我们创建霍夫曼树的时左节点都为叶子节点),否则走右节点,这样将N分类问题转化成至多做N次二分类。
霍夫曼树词频高的词所在的叶子节点更接近于根节点,因此树深处的叶子节点基本都为长尾词,不太可能被遍历到。另外霍夫曼树在某个非叶子节点,一旦左右分支两边的概率都低于上方的某个叶子节点(比如第一次分裂,左叶子:0.4,右边:0.6,走右边; 第二次分类:左边0.4,右边0.6,则总体概率左边0.6 * 0.4 = 0.24,右边0.6* 0.6=0.36,都小于第一次的左叶子节点0.4,那么第一个左叶子节点上的词即为最大可能的预测词)。因此使用这两种特性,可以很快的不经过N次二分类就找到正确的预测词。
注意,word2vec不仅要优化softmax的参数,还要优化输入词的词向量,因为他的真实模型类似与一个只有一个hidden layer + 全连接层的神经网络
这里的输入是skip-gram中心词的one-hot编码,而上面所说的霍夫曼树的输入是input vector与第一层hidden layer所连接的权重,(hidden layer有300个神经元,则每个word有300维权重,即300维词向量),因此根据反向传播,先优化softmax参数,再优化第一层隐层的链接权重。
9. 有几个 G 的文本,每行记录了访问 ip 的 log ,如何快速统计 ip 出现次数最高的 10 个 ip ;如果只用 linux 指令又该怎么解决;
hive,count(*) 之后 order limit 就可以,或者row number取前10
linux:假设文件为a.txt,第一列为ip
cat a.txt |cut -f1 |sort |uniq -c |sort -nrk1 |head -10
分别是取第一列,排序+统计|根据统计结果第一列排序|取前10
10. LR的损失函数
LR解决的是二分类问题,具体的样本label分布为伯努利分布,即一个样本为(1,0)正类或(0,1)负类,交叉熵可以评估两个分布之间的差距,因此自然可以作为LR的损失函数。
交叉熵:
对于真实分布与非真实分布,计算公式为
假设对于一条样本,做二分类,真实分布为(1,0) = (y,1-y) 模型预测为正类的打分为0.7 =p(sigmoid),则模型预测分布为(0.7,0.3) = (p,1-p),
则交叉熵为1 * log2(1/0.7) + 0 * log2(1/0.3) = 0.356
1 * log2(1/0.7) + 0 * log2(1/0.3) = 1* log2(1) - 1* log2(0.7) + 0 * log2(1) - 0 * log2(0.3) = - (1 * log2(0.7) + 0 * log2(0.3))
更一般的形式
y * log2(1/p) + (1-y) * log2(1/(1-p)) = y* log2(1) - y* log2(p) + (1-y) * log2(1) - (1-y) * log2(1-p)
= - (y * log2(p) + (1-y) * log2(1-p))
该交叉熵的最终形式 - (y * log2(p) + (1-y) * log2(1-p))是LR的损失函数。
逻辑回归的损失也可以从极大似然估计上来理解,的对数似然函数:
似然函数为所有样本正确分类概率的乘积
对数似然函数为似然函数求log,结果为
括号内部对于单条样本的似然函数的值即为对于该条样本,真实分布与非真实分布的交叉熵的负数
因此:最大化似然函数 = 减少交叉熵(交叉熵越小,与真实分布约接近,交叉熵最小为真实分布的熵,对于二分类,真实分布(1,0)的熵为0)
在逻辑回归里的说法:
•最大化对数似然函数 = 最小化损失函数
通常将上式中的对数似然函数取一个符号,作为损失函数,即如下式子
可见,该式子与上面标红的交叉熵计算公式是一致的。
因此,LR的损失函数又叫做交叉熵损失函数。
11. LR为什么使用logloss损失函数,而不是RMSE函数
- LR是伯努利分布,评估分布的差别用交叉熵更为合理,RMSE常用于回归问题,因为回归问题的目标倾向于正态分布。
- 如果一定要用RMSE,可以自己求导发现,RMSE的梯度是误差的二次方,logloss是误差的一次方,即实际label为1,LR预测为0.95,则梯度是0.05, 则要对参数的每一项加0.05 * 学习率。如果是RMSE,梯度是0.05 * 0.05 = 0.0025, 更新效率太低。
12. 常见sentence embedding方法
- bags of words / bags of n-grams 通过句子覆盖的词频来定义句子向量
- 对一个句子里的word的vector直接求sum/avg
- sentence embedding 论文做法,类似于cbow,拿sentence vector(random intializer) + 前n个词的vector去predict下一个词的vector,类似于word2vec的神经网络模型。
第二种,类似于skip-gram,拿每个sentence vector 去预测一个词的vector。训练得到sentence vector。
13.梯度下降的优缺点;
优化思想
当目标函数是凸函数时,梯度下降法的解是全局解。一般情况下,其解不保证是全局最优解,梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是”最速下降法“。最速下降法越接近目标值,步长越小,前进越慢。
缺点
梯度下降法的最大问题就是会陷入局部最优,靠近极小值时收敛速度减慢。
批量梯度下降法
最小化所有训练样本的损失函数,使得最终求解的是全局的最优解,即求解的参数是使得风险函数最小,但是对于大规模样本问题效率低下。
随机梯度下降法
最小化每条样本的损失函数,虽然不是每次迭代得到的损失函数都向着全局最优方向, 但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近,适用于大规模训练样本情况。
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将theta迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
14. 为什么说bagging是减少variance,而boosting是减少bias?
从机制上讲
为什么说bagging是减少variance,而boosting是减少bias
若各子模型独立,则有$Var(\frac{\sum X_i}{n})=\frac{Var(X_i)}{n}$,此时可以显著降低variance。若各子模型完全相同,则$Var(\frac{\sum X_i}{n})=Var(X_i)$,此时不会降低variance。
Bagging 是 Bootstrap Aggregating 的简称,意思就是再取样 (Bootstrap) 然后在每个样本上训练出来的模型取平均。,所以从偏差上看没有降低,但是由于各个子模型是单独训练的,有一定的独立性,所以方差降低比较多,提高泛化能力。特别是random forest这种方式,不仅对样本取样,还有特征取样。
boosting从优化角度来看,是用forward-stagewise这种贪心法去最小化损失函数,在这个过程中偏差是逐步减小的,而由于各阶段分类器之间相关性较强,方差降低得少。
举个例子
gbdt是boosting的方式,它的决策树的深度比较小,模型会欠拟合,刚开始偏差大,后来就慢慢变小了。
15. XGBoost常用的评价指标与调节参数
logloss: 评价binary logistic目标的常用损失
AUC: 评价二分类问题的排序能力
AUC值的一种解释是,给定一个正样本和一个负样本,模型打分正样本比负样本分高的概率,就是AUC值
RMSE ,MAE 均方误差、绝对误差 :评估回归问题
NDCG,MAP 一般评价搜索RANK问题
调节参数
- 树的个数、深度
- 学习率
- 行采样率,列采样率
- min_child_weight 每个叶子节点的最小权重
xgboost为什么对离散的稀疏特征one-hot效果不好
主要是树的个数与深度限制,假设100颗树,深度为6,则一共只有几千个分割节点,如果用离散特征,动辄就是上万维度,整个model也覆盖不了多少特征。
- SGD/ Momentum / adagrad
http://blog.csdn.net/blue_jjw/article/details/50650248
SGD指stochastic gradient descent,即随机梯度下降。是梯度下降的batch版本。
这么做的好处在于:
当训练数据太多时,利用整个数据集更新往往时间上不显示。batch的方法可以减少机器的压力,并且可以更快地收敛。
当训练集有很多冗余时(类似的样本出现多次),batch方法收敛更快。以一个极端情况为例,若训练集前一半和后一半梯度相同。那么如果前一半作为一个batch,后一半作为另一个batch,那么在一次遍历训练集时,batch的方法向最优解前进两个step,而整体的方法只前进一个step。
momentum :SGD对参数的更新完全依赖于当前的batch,因此加入了momentum来保存上一步更新的一些影响
adagrad: 随着参数移动距离的增大,降低学习率,这样对于每个不同的参数(比如有的参数覆盖的样本少,更新的次数少,因此还要保证大的学习率,而已经更新很多遍的参数对应一个小的学习率)有着不同的学习率
Adadelta
Adagrad算法存在三个问题
其学习率是单调递减的,训练后期学习率非常小
其需要手工设置一个全局的初始学习率
更新xt时,左右两边的单位不同一