Codeforces Round #195 A B C 三题合集 (Div. 2)
A 题 Vasily the Bear and Triangle
题目大意
一个等腰直角三角形 ABC,角 ACB 是直角,AC=BC,点 C 在原点,让确定 A 和 B 的坐标,使得三角形包含一个矩形,这个矩形一个角在原点,另一个点在 (x, y) 处,并且三角形 ABC 的面积尽量小
将 A B 两点按照 x 坐标从小到大输出
做法分析
A B 两点必然在坐标轴上,且线段 AB 经过点 (x, y),那么简单分类讨论下就行了
交之前犹豫了一下,10分钟才提交...
参考代码

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 5 using namespace std; 6 7 const int N=1000006; 8 9 int x, y; 10 11 int main() { 12 scanf("%d%d", &x, &y); 13 if(x>0 && y>0 || x<0 && y<0) { 14 if(x<0) { 15 printf("%d %d %d %d\n", x+y, 0, 0, x+y); 16 } 17 else { 18 printf("%d %d %d %d\n", 0, x+y, x+y, 0); 19 } 20 } 21 else { 22 if(x<0) { 23 printf("%d %d %d %d\n", x-y, 0, 0, y-x); 24 } 25 else { 26 printf("%d %d %d %d\n", 0, y-x, x-y, 0); 27 } 28 } 29 return 0; 30 }
B 题 Vasily the Bear and Fly
题目大意
在平面上有 2*m(1≤m≤105) 个同样半径的圆。他们编号分别为 1~2*m,分上下两排排列.
第 1 到 m 个圆的圆心坐标分别为:(2R-R, 0), (4R-R, 0),...,(2mR-R, 0)
第 m+1 到第 m+m 个圆的圆心坐标分别为:(2R-R, 2R), (4R-R, 2R),...,(2mR-R, 2R)
有一只 fly(苍蝇?)在这个平面上运动了 m2 次,这 m2 次运动分别编号为 0~(m2-1),编号为 i 的那次运动从第 1+i/m 个圆的圆心运动到第 m+1+i%m 个圆的圆心,且走最短路,fly 走过的路径必须包含在这 2*m 个圆确定的区域中,不能走到外面的其他地方
现在问,这只 fly 的 m2 次运动中,每次运动走过的平均距离是多少
做法分析
典型的数学题,当时看见,菊花莫名其妙的一紧,脚趾头都抓紧了......
观察这 2*m 个圆的圆心坐标不难发现,他们分成了上下两排,同一排相邻的两个圆相切,上下相邻的两个圆相切
再观察 fly 每次运动走的圆的分布规律,不难发现是每次选定一个下面的圆的圆心,分别以上面的圆的圆心为目的点走一次最短路,所以总共有 m2 次运动
那么一个最通常的想法就是:求出这 m2 次运动总共走过的距离
先看看最短路吧:
由于每次一定是一个圆在下面,一个圆在上面,那么可以这样搞:
当两个圆相邻时(列号差为 0),最短路是 2R
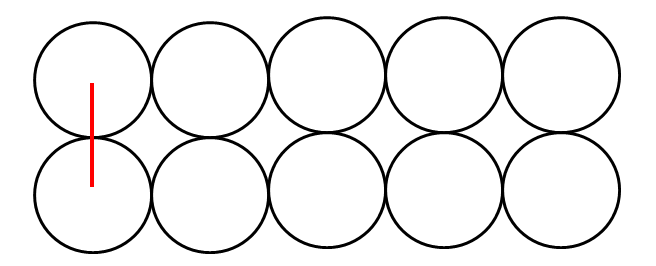
当两个圆的列号差为 1 时,最短路是 2R+√2R
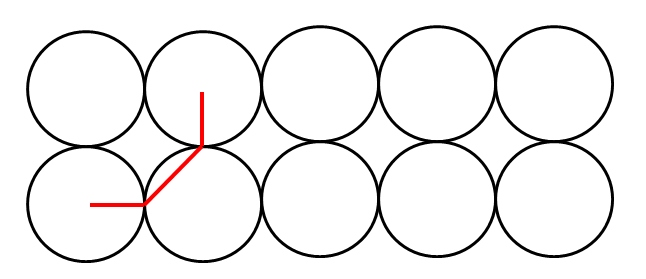
当两个圆的列号差为 2 时,最短路是 2R+2√2R
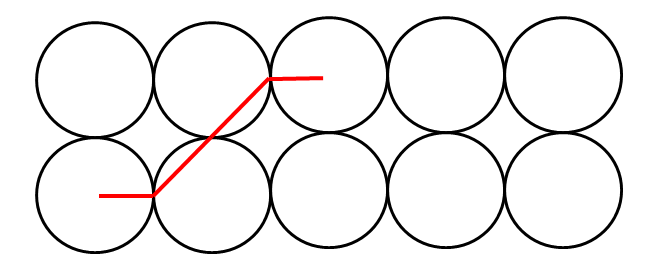
当两个圆的列号差为 3 时,最短路是 4R+2√2R
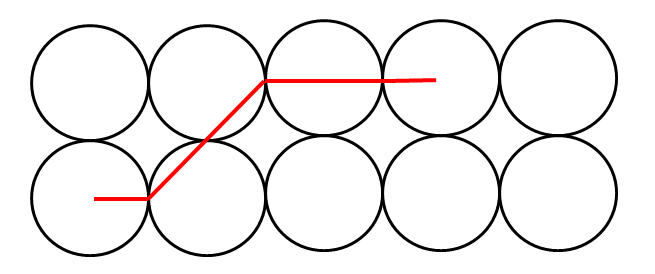
当两个圆的列号差为 4 时,最短路是 6R+2√2R
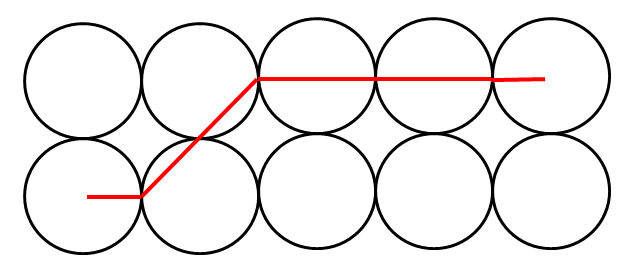
当两个圆的列号差为 5 时,最短路是 8R+2√2R
......
将他们存进一个数组 A 中,A[i] 表示列号差为 i 的最短路长度
以 m 为单位,看看每次运动的起始点和终止点
前 m 次运动:起始点始终是下面第 1 个圆,终止点从上面第 1 个圆变化到第 m 个圆
接下来的 m 次运动:起始点始终是下面第 2 个圆,终止点从上面第 1 个圆变化到第 m 个圆
再接下来的 m 次运动:起始点始终是下面第 3 个圆,终止点从上面第 1 个圆变化到第 m 个圆
......
细心的读者在这里的时候估计已经知道该怎么做了,还没想出来的朋友可以接着往下看
从上面可以看出:起始点是在不停的往前走的,而终止点始终是上面的圆从 1 到 m
我们再以 m 为单位,看看他们的距离和
前 m 次运动的距离和我们可以求出来:sum1=∑A[i]
那么接下来的 m 次运动的距离和呢:sum2=sum-A[m-1]+A[1]
再接下来的的 m 次运动的距离和呢:sum3=sum2-A[m-2]+A[2]
第 4 个 m 次运动的距离和:sum4=sum3-A[m-3]+A[3]
......
相信看到这里,大家都知道该怎么做了 o(m) 的扫一遍,用两个指针辅助,这样就可以求出来了
参考代码

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 #include <cmath> 5 6 using namespace std; 7 8 const int N=100006; 9 10 int m; 11 double R, A[N]; 12 13 void init() { 14 A[0]=2, A[1]=2+sqrt(2); 15 for(int i=2; i<m; i++) A[i]=2*(i-1)+2*sqrt(2); 16 } 17 18 int main() { 19 scanf("%d%lf", &m, &R); 20 init(); 21 double ans=0; 22 for(int i=0; i<m; i++) { 23 ans+=A[i]; 24 } 25 int p1=1, p2=m-1; 26 double last=ans; 27 for(int i=1; i<m; i++) { 28 last=last-A[p2]+A[p1]; 29 ans+=last; 30 p1++, p2--; 31 } 32 printf("%lf\n", ans/m/m*R); 33 return 0; 34 }
C 题 Vasily the Bear and Sequence
题目大意
给了 n(1≤n≤105) 个不同的数,要求选出一些数出来,使得这些数按位取与之后的数在二进制下,最低位的 1 所在的位尽量高,如果有多重方案,输出选取数的数量最大的一个方案
做法分析
初一看很神,其实仔细想一下不难发现这题比 B 题还水...
考虑最后选取的数按位取与之后得到的数,设为 sum
要使 sum 在二进制下 1 的最低位最高,也就是说,这一位 1 以后,所有的数都应该是 0
想到这里,反应比较快的读者肯定知道该怎么做了
枚举最低位,设为 pos,先在所有数中选出二进制表示下,在 pos 位为 1,的那些数,如果这些数按位取与,能够使得所有低于 pos 位的二进制位全为 0,那么这些数就是一个合法的答案,当然,如果我们是从高位往地位枚举的,这些数就是我们最后的答案了
参考代码

1 #include <cstring> 2 #include <cstdio> 3 #include <iostream> 4 5 using namespace std; 6 7 int A[100005], n; 8 bool vs[100005]; 9 10 int main() { 11 scanf("%d", &n); 12 for(int i=0; i<n; i++) scanf("%d", &A[i]); 13 for(int i=31; i>=0; i--) { 14 bool flag=1; 15 memset(vs, 0, sizeof vs); 16 for(int j=0; j<n; j++) if(A[j]&(1<<i)) vs[j]=1; 17 for(int pos=i-1; pos>=0 && flag; pos--) { 18 bool all=0; 19 for(int j=0; j<n && !all; j++) if(vs[j]) { 20 if(!(A[j]&(1<<pos))) all=1; 21 } 22 if(!all) flag=0; 23 } 24 if(flag) break; 25 } 26 int cnt=0; 27 for(int i=0; i<n; i++) if(vs[i]) cnt++; 28 printf("%d\n", cnt); 29 for(int i=0; i<n; i++) if(vs[i]) { 30 printf("%d", A[i]); 31 cnt--; 32 if(!cnt) printf("\n"); 33 else printf(" "); 34 } 35 return 0; 36 }
