并查集

文章来源：勇幸|Thinking (http://www.ahathinking.com)  

昨天和今天学习了并查集和trie树，并练习了三道入门题目，理解更为深刻，觉得有必要总结一下，这其中的内容定义之类的是取自网络，操作的说明解释及程序的注释部分为个人理解。

    并查集学习：

• 并查集：(union-find sets)

一种简单的用途广泛的集合. 并查集是若干个不相交集合，能够实现较快的合并和判断元素所在集合的操作，应用很多，如其求无向图的连通分量个数等。最完美的应用当属：实现Kruskar算法求最小生成树。

• 并查集的精髓（即它的三种操作，结合实现代码模板进行理解）：

1、Make_Set(x) 把每一个元素初始化为一个集合

初始化后每一个元素的父亲节点是它本身，每一个元素的祖先节点也是它本身（也可以根据情况而变）。

2、Find_Set(x) 查找一个元素所在的集合

查找一个元素所在的集合，其精髓是找到这个元素所在集合的祖先！这个才是并查集判断和合并的最终依据。
判断两个元素是否属于同一集合，只要看他们所在集合的祖先是否相同即可。
合并两个集合，也是使一个集合的祖先成为另一个集合的祖先，具体见示意图

3、Union(x,y) 合并x,y所在的两个集合

合并两个不相交集合操作很简单：
利用Find_Set找到其中两个集合的祖先，将一个集合的祖先指向另一个集合的祖先。如图

 

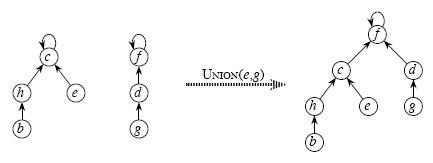
• 并查集的优化

1、Find_Set(x)时 路径压缩
寻找祖先时我们一般采用递归查找，但是当元素很多亦或是整棵树变为一条链时，每次Find_Set(x)都是O(n)的复杂度，有没有办法减小这个复杂度呢？
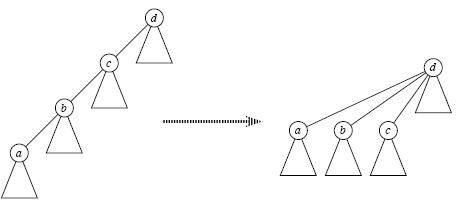
答案是肯定的，这就是路径压缩，即当我们经过"递推"找到祖先节点后，"回溯"的时候顺便将它的子孙节点都直接指向祖先，这样以后再次Find_Set(x)时复杂度就变成O(1)了，如下图所示；可见，路径压缩方便了以后的查找。

2、Union(x,y)时 按秩合并
即合并的时候将元素少的集合合并到元素多的集合中，这样合并之后树的高度会相对较小。

 

• 主要代码实现

 1 注意：

 2 代码中路径压缩时秩不需变化的，正如Eillen所说，秩只是表示节点高度的一个上界

 3 如果用秩进行计数，路径压缩也是不需要变化的

 4 因为所属集合的根节点的秩在合并时已经更新，其他子节点的秩不用到也无需再变化；

 5 int father[MAX];   /* father[x]表示x的父节点*/

 6 int rank[MAX];     /* rank[x]表示x的秩*/

 7  

 8 /* 初始化集合*/

 9  

10 void Make_Set(int x)

11 {

12     father[x] = x; //根据实际情况指定的父节点可变化

13     rank[x] = 0;   //根据实际情况初始化秩也有所变化

14 }

15  

16 /* 查找x元素所在的集合,回溯时压缩路径*/

17  

18 int Find_Set(int x)

19 {

20     if (x != father[x])

21     {

22         father[x] = Find_Set(father[x]); //这个回溯时的压缩路径是精华

23     }

24     return father[x];

25 }

26  

27 /*

28 按秩合并x,y所在的集合

29 下面的那个if else结构不是绝对的，具体<strong>根据实际情况</strong>变化

30 但是，宗旨是不变的即，按秩合并，实时更新秩。

31 */

32  

33 void Union(int x, int y)

34 {

35     x = Find_Set(x);

36     y = Find_Set(y);

37     if (x == y) return;

38     if (rank[x] > rank[y])

39     {

40         father[y] = x;

41         rank[x] += rank[y];

42     }else

43     {

44         if (rank[x] == rank[y])

45         {

46             rank[y]++;

47         }

48         father[x] = y;

49     }

50 }

 

并查集简单使用：

假如已知有n个人和m对好友关系（存于数字r）。如果两个人是直接或间接的好友（好友的好友的好友...），则认为他们属于同一个朋友圈，请写程序求出这n个人里一共有多少个朋友圈。

假如：n = 5 ， m = 3 ， r = {{1 , 2} , {2 , 3} , {4 , 5}}，表示有5个人，1和2是好友，2和3是好友，4和5是好友，则1、2、3属于一个朋友圈，4、5属于另一个朋友圈，结果为2个朋友圈。

http://ac.jobdu.com/problem.php?pid=1526

输入：

输入包含多个测试用例，每个测试用例的第一行包含两个正整数 n、m，1=<n，m<=100000。接下来有m行，每行分别输入两个人的编号f，t（1=<f，t<=n），表示f和t是好友。 当n为0时，输入结束，该用例不被处理。

 

输出：

对应每个测试用例，输出在这n个人里一共有多少个朋友圈。

 

样例输入：

5 3

1 2

2 3

4 5

3 3

1 2

1 3

2 3

0

样例输出：

2

1

 1 public class Main {

 2     public static void main(String[] args) throws IOException {

 3         circleOfFriends();

 4     }

 5 

 6     public static void circleOfFriends() throws IOException {

 7         int sum = 0;

 8         BufferedReader reader = new BufferedReader(new InputStreamReader(

 9                 System.in));

10         String input = null;

11         while (!(input = reader.readLine()).equals("0")) {

12             StringTokenizer st = new StringTokenizer(input);

13             int n = Integer.parseInt(st.nextToken());

14             int m = Integer.parseInt(st.nextToken());

15 

16             int[] father = new int[n + 1];

17             int[] rank = new int[n + 1];

18             for (int i = 1; i < n + 1; i++) {

19                 father[i] = i;

20                 rank[i] = 1;

21             }

22 

23             for (int i = 0; i < m; i++) {

24                 st = new StringTokenizer(reader.readLine());

25                 int a = Integer.parseInt(st.nextToken());

26                 int b = Integer.parseInt(st.nextToken());

27                 union(father, rank, a, b);

28             }

29 

30             for (int i = 1; i < n + 1; i++) {

31                 sum += rank[i];

32             }

33             System.out.println(sum);

34             sum = 0;

35         }

36     }

37 

38     public static int findSet(int[] father, int x) {

39         if (x != father[x]) {

40             father[x] = findSet(father, father[x]);

41         }

42         return father[x];

43     }

44 

45     public static void union(int[] father, int[] rank, int a, int b) {

46         int fa = findSet(father, a);

47         int fb = findSet(father, b);

48         if (fa == fb) {

49             return;

50         }

51 

52         rank[fb] = 0;

53         father[fb] = fa;

54     }

55 }

 

 

更多并查集的应用可以参见下面的链接：

并查集(Union-Find) 应用举例 --- 基础篇