数学图形之圆柱面
这一节将为你展示如何生成圆柱面,以及和圆柱面相关的图形,如鼓形,齿轮等
相关软件参见:数学图形可视化工具,使用自己定义语法的脚本代码生成数学图形.
我之前写过生成圆柱的C++程序,代码发布在柱台(Cylinder)图形的生成算法.
(1)圆柱面
vertices = dimension1:72 dimension2:72 u = from 0 to (2*PI) dimension1 v = from (-5) to (5) dimension2 r = 5 x = r*cos(u) y = v z = r*sin(u)
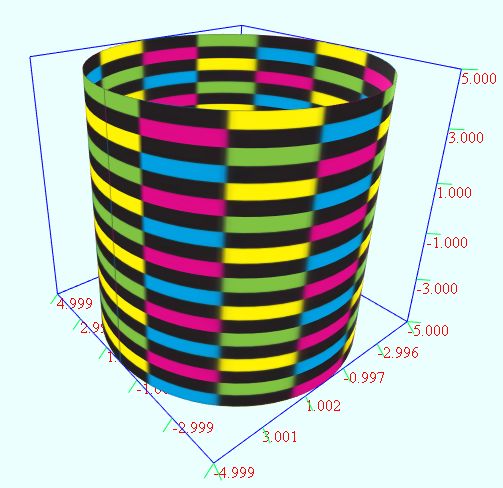
(2)任意角度圆柱面
vertices = dimension1:72 dimension2:72 u = from (-5) to (5) dimension2 v = from 0 to (2*PI) dimension1 a = rand2(0, 2*PI) b = rand2(0, 2*PI) c = sin(v) d = cos(v) e = sin(b) f = cos(b) g = sin(a) h = cos(a) x = f*h*d - f*g*c + e*u y = g*d + h*c z = -e*h*d + e*g*c + f*u x = x*5 y = y*5 z = z*5
代码中会随机设置圆柱的旋转角度

(3)圆柱体
将圆柱面的两头封上,生成闭合的圆柱体
vertices = dimension1:72 dimension2:72 u = from 0 to (2*PI) dimension1 v = from (-5) to (5) dimension2 r = if(abs(v) < 4.9, 5, 0) x = r*cos(u) y = v z = r*sin(u)
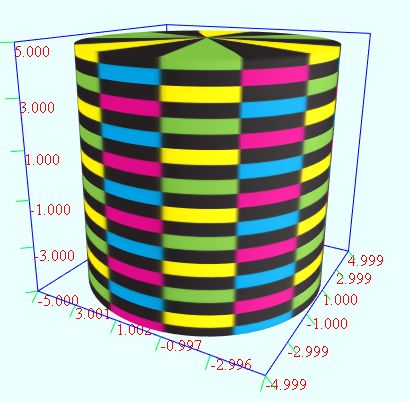
(4)由曲线生成的圆柱面
#http://www.mathcurve.com/surfaces/cylindrederevolution/cylindrederevolution.shtml vertices = D1:100 D2:100 u = from 0 to (2*PI) D1 v = from 0 to (PI) D2 a = rand2(1, 10) x = a*cos(u - v) z = a*sin(u - v) y = a*( u+v)

(5)鼓形
我之前写过生成鼓形的C++程序,代码发布在鼓状物(Drum)图形的生成算法
这里和之前的不太一样,为了简单,我对鼓的隆起使用了SIN函数.
vertices = dimension1:72 dimension2:72 u = from 0 to (2*PI) dimension1 v = from (-1) to (1) dimension2 r = 5 h = rand2(1, r) t = h*cos(v*PI/2) p = if(t > 0.01, r+t, 0) x = p*cos(u) y = v*h z = p*sin(u)
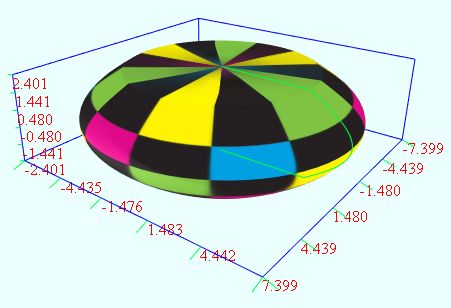
新的鼓形脚本,这个比上一个要圆润得多:
vertices = dimension1:72 dimension2:72 u = from 0 to (2*PI) dimension1 v = from (-PI/2) to (PI/2) dimension2 r = 5 h = rand2(1, r) t = h*cos(v) p = if(t > 0.01, r+t, 0) x = p*cos(u) y = h*sin(v) z = p*sin(u)
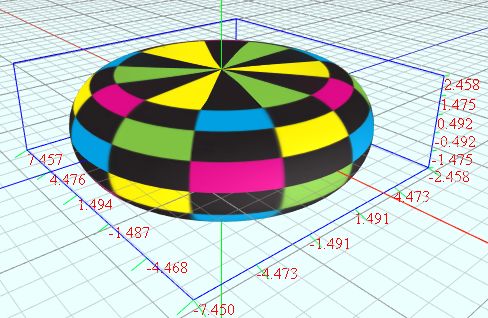
(6)齿轮
我之前写过生成齿轮的C++程序,代码发布在齿轮(Gear Wheel)图形的生成算法
vertices = D1:65 D2: 4 u = from 0 to (2*PI) D1 v = from -1 to 1 D2 k = from 0 to 64 D1 m = mod(k, 2) r = 10.0 + m*2 a = 0.9 b = in_range(v, -a, a) x = r*sin(u)*b z = r*cos(u)*b y = if(b, v, v/3)*3

(7)刺柱
为什么我看到这个有刺的柱子,会想到满清十大酷刑.
vertices = D1:129 D2:65 u = from 0 to (2*PI) D1 v = from (-20) to (20) D2 n = 4 a = from 0 to 128 D1 b = from 0 to 64 D2 t = (mod(a, n) + mod(b, n))/n*4 r = 10 + t x = r*cos(u) y = v z = r*sin(u)

(8)蛏形
vertices = D1:100 D2:100 u = from 0 to (2*PI) D1 v = from -5 to 5 D2 r = 5 x = r*cos(u) z = r*sin(u) y = x*v

(9)指定方向的圆柱(极坐标原理)
vertices = dimension1:72 dimension2:72 u = from (0) to (5) dimension2 v = from 0 to (2*PI) dimension1 a = rand2(-2, 2) b = rand2(-2, 2) c = rand2(-2, 2) ac = sqrt(a*a + c*c) angleY = atan2(ac, b) angleXZ = atan2(a,c) m = cos(v) n = sin(v) e = sin(angleY) f = cos(angleY) g = sin(angleXZ) h = cos(angleXZ) x0 = m y0 = u*f - n*e z0 = u*e + n*f x1 = x0*h + z0*g y1 = y0 z1 = -x0*g + z0*h x = x1 + a y = y1 + b z = z1 + c
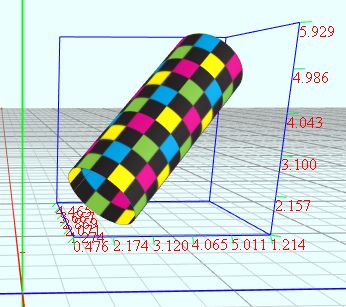
(10)指定方向的圆柱(矩阵原理)
vertices = dimension1:72 dimension2:72 u = from (0) to (5) dimension2 v = from 0 to (2*PI) dimension1 a = rand2(-2, 2) b = rand2(-2, 2) c = rand2(-2, 2) len = sqrt(a*a + b*b + c*c) len = max(len, 0.00001) px = a/len py = b/len pz = c/len qx = 0 qy = pz qz = -py len = sqrt(qx*qx + qy*qy + qz*qz) len = max(len, 0.00001) qx = qx/len qy = qy/len qz = qz/len wx = py*qz - pz*qy wy = pz*qx - px*qz wz = px*qy - py*qx x0 = cos(v) y0 = u z0 = sin(v) x = x0*wx + y0*px + z0*qx + a y = x0*wy + y0*py + z0*qy + b z = x0*wz + y0*pz + z0*qz + c
