论文笔记——对NLP深度神经模型的统一深入理解【神经网络可解释性】

From SJTU, MSRA and PKU.
Authors: Chaoyu Guan, Xiting Wang, Quanshi Zhang, Runjin Chen, Di He, Xing Xie.
Title: Towards a Deep and Unified Understanding of Deep Neural Models in NLP
In: ICML 2019.
Codes: icml2019paper2428/Towards-A-Deep-and-Unified-Understanding-of-Deep-Neural-Models-in-NLP

Introduction

前段时间看过张拳石老师介绍这篇论文的文章，很感兴趣，自己原来也有这方面的其他想法，但是并没有实践过，这篇论文收获颇丰。

不管是深度学习的哪个方向，深度神经网络（DNN）的可解释性一直是一个困扰我们的问题。基于DNN的NLP模型效果为什么好？貌似没有一个好的解释方法。之前有几个尝试性的工作：

• gradient-based：基于梯度的方法
• inversion-based：基于反演的方法
• layer-wise relevance propagation：相关性逐层传播

这些方法一定程度上定量分析了模型的中间层，虽然可以进一步理解神经网络的内部机制，但是存在not coherency（“普适性”）和not generality（“一贯性”）问题：

• 普适性：解释性指标的计算算法尽可能独立于神经网络结构和目标任务的选择。比如，对单个神经元的分析适用，也要对神经元组成的网络层适用，还要对整个模型适用。
• 一贯性：解释性指标需要客观地反应特征的表达能力，并实现对不同模型结构和任务的广泛比较，也就是解释性指标的“泛化能力”。

文章试图找到一个可以定量分析（解释/可视化）NLP神经网络模型的方法，利用互信息[3]这一具有“普适性”特点的信息度量，定义了一种统一的information-based measure，量化NLP深度神经模型中的中间层对每个词编码的信息，研究每个单词的信息遗忘程度。

Methods

文章想从两个角度解释中间层的隐层状态：word information quantification【词信息定量分析】和fine-grained analysis of word attributes【细粒度词属性分析】。

Word Information Quantification

定量计算隐层状态编码输入词的信息量：

corpus-level:
$$MI(\mathbf{X};\mathbf{S})=H(\mathbf{X})-H(\mathbf{X}|\mathbf{S})$$
MI是互信息，H是熵。对于同一个输入，H(X)是恒量，模型中每一层每一个神经元对输入X对编码程度不一样，用H(X|S)表示隐层S丢弃X的信息量，MI就是S编码X的信息量。

其中： $$H(\mathbf{X}|\mathbf{S})={\int }_{\mathbf{s}\in \mathbf{S}}p(\mathbf{s})H(\mathbf{X}|\mathbf{s})d\mathbf{s}$$

sentence-level:

$$H(\mathbf{X}|\mathbf{s})=-{\int }_{{\mathbf{x}}^{\prime }\in \mathbf{X}}p\left({\mathbf{x}}^{\prime }|\mathbf{s}\right)\log p\left({\mathbf{x}}^{\prime }|\mathbf{s}\right)d{\mathbf{x}}^{\prime }$$
其中：$$\mathbf{s}=\Phi (\mathbf{x})$$ 表示x对应的隐层状态。用H(X|s)表示中间层中对应的隐层状态集s丢弃X的信息量。

word-level:

$$H(\mathbf{X}|\mathbf{s})=\sum _{i}H\left({\mathbf{X}}_i|\mathbf{s}\right)H\left({\mathbf{X}}_i|\mathbf{s}\right)=-{\int }_{{\mathbf{x}}_i^{\prime }\in {\mathbf{X}}_i}p\left({\mathbf{x}}_i^{\prime }|\mathbf{s}\right)\log p\left({\mathbf{x}}_i^{\prime }|\mathbf{s}\right)d{\mathbf{x}}_i^{\prime }$$

其中$X_i$表示第i个词的向量。

在计算word-level信息量时，概率 $p\left({\mathbf{x}}_i^{\prime }|\mathbf{s}\right)$ 很难算，这部分详见论文[2]3.2.2节和补充材料。为了便于计算，文章引入了perturbation-based approximation【扰动近似】。核心思想就是给每个词加一个高斯扰动项 ${\tilde{\mathbf{x}}}_i={\mathbf{x}}_i+{\mathbf{ϵ}}_i$，经过近似之后，目标函数变换成求极值问题：
$$L(\mathbf{\sigma })=\sum _{i=1}^n\left(-\log {\sigma }_i\right)+\frac{1}{K\lambda }{\mathbb{E}}_{{\tilde{\mathbf{x}}}_i\cdot {\mathbf{ϵ}}_i\sim \mathcal{N}\left(0,{\sigma }_i^2\mathbf{I}\right)}\frac{\Vert \Phi (\tilde{\mathbf{x}})-\mathbf{s}{\Vert }^2}{{\sigma }_{\mathbf{S}}^2}$$

这里把补充材料的例子搬过来，更容易理解，扰动项就是解释指标的关键。

目标函数分为两部分：

左边部分是给每一个词向量加扰动， $\sigma$ 越大，说明这个词需要丢弃的信息越多【也就是这个词越不重要】；

右边部分是经过DNN编码之后，加扰动之后输入，经过DNN编码得到的 $\Phi (\tilde{\mathbf{x}})$ 要与原始输入的 s 差距越小越好。

按照这个最优化目标，学习得到的扰动项可以很好地表示词的重要程度。

Fine-Grained Analysis of Word Attributes

这部分分析了神经网络中间层的每个输入词内部的细粒度属性信息，属性来自DBpedia和Microsoft Concept Graph，概念 c （例如，情感形容词）由属于该概念的一组词组成（例如，happy，sorrowful，sad，…）。对于每一个词 x_i ，通过计算 s 编码当前词相对于随机词的相对置信度，将共同概念 c 中的信息从目标词的所有信息中解放出来。Figure_8对这方面做了实验。
近似计算 s 编码当前词 x_i （当前词是概念，在 c 中）相对于随机词 $x_i^{\prime }$ 的相对置信度 A_i 和 A_c ：
$$A_i=\log p\left({\mathbf{x}}_i|\mathbf{s}\right)-{\mathbb{E}}_{{\mathbf{x}}_i^{\prime }\in {\mathbf{X}}_i}\log p\left({\mathbf{x}}_i^{\prime }|\mathbf{s}\right)$$
$$A_{\mathrm{c}}={\mathbb{E}}_{{\mathbf{x}}_i^{\prime }\in {\mathbf{X}}_{\mathrm{c}}}\log p\left({\mathbf{x}}_i^{\prime }|\mathbf{s}\right)-{\mathbb{E}}_{{\mathbf{x}}_i^{\prime }\in {\mathbf{X}}_i}\log p\left({\mathbf{x}}_i^{\prime }|\mathbf{s}\right)$$
然后在将两项做差，表示当前词x_i 去掉共有属性 c 之后的剩余信息：
$$r_{i,c}=A_i-A_{\mathbf{c}}=\log p\left({\mathbf{x}}_i|\mathbf{s}\right)-{\mathbb{E}}_{{\mathbf{x}}_i^{\prime }\in {\mathbf{X}}_{\mathrm{c}}}\log p\left({\mathbf{x}}_i^{\prime }|\mathbf{s}\right)$$

Experiment

第一部分实验分别跨时间戳、图层和模型，评价基于信息的解释方法。对比基准有：

• LRP，给任意两个神经元的相关度打分，这里用的是隐层状态与输入词向量的绝对值。
• Perturbation，是CV里的一种方法，这里直接把输入句子当作图像来处理。
• Gradient，使用一阶导数的绝对值来表示每个输入词的重要性，这里将词向量每一维的一阶导数的绝对值求平均，得到词的重要性度量。

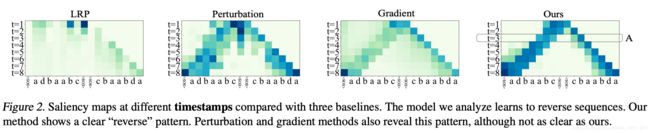
Across Timestamp Analysis

实验可视化分析reverse sequence【逆向序列】神经网络中层特征关注点的区别，基于词信息量的方法，可以更加平滑自然的显示神经网络内部信息处理逻辑。其他方法也还可以，LRP方法就难以显示。

Across Layer Analysis

实验可视化分析了不同解释方法在SST2任务上神经网络中层特征关注点的区别。基于词信息量的方法，可以更加平滑自然的显示神经网络内部信息处理逻辑。结果表明，LRP和Gradient实效了，Perturbation噪音很大。

Across Model Analysis

实验研究了超参数的不同选择如何影响模型学习的隐藏状态。结果表明，基于词信息量的方法可以快速识别大学习率的模型包含的信息太少，应该减少学习率来改善性能。相比之下，Gradient方法不能在超参数调整方面提供类似的指导。

Understanding Neural Models in NLP

第二组实验分析比较了四种在NLP中常用的深度学习模型，即BERT、Transformer、LSTM和CNN，BERT为什么效果最好呢？文章有了初步解释，相比于LSTM和CNN，BERT和Transformer往往可以更加精确地找到与任务相关的目标单词，而CNN和LSTM往往使用大范围的词去做预测，没有聚焦。

并且，BERT模型在预测过程中往往使用具有实际意义的单词作为分类依据，而其他模型把更多的注意力放在了and/the/to/is/that 这类缺少实际意义的单词上。

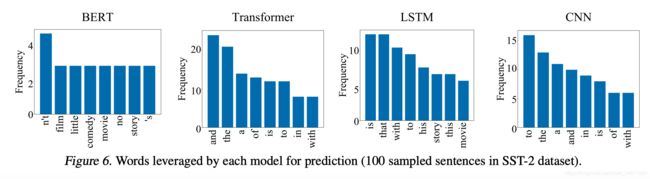
在SST-2任务上，BERT模型在L3-L4层就已经遗忘了EOS单词，往往在第5到12层逐渐遗忘其他与情感语义分析无关的单词。相比于其他模型，BERT模型在单词选择上更有针对性，没有预训练的Transformer每次都照顾到所有的词，LSTM更关注前面的词，CNN基本上就是眉毛胡子一把抓。

前面提到的细粒度词属性信息，这里分析了各个单词的概念信息遗忘。BERT模型对各种细粒度概念信息保留得最好，曲线平缓。

最后还有一个实验展示了在LSTM和BERT的所有层的训练过程中，互信息是如何变化的。可以看到，BERT的互信息变化很稳定，最后几层在2500层之前压缩信息，达到稳定状态。LSTM一开始让更多的信息通过，然后再抛弃无用信息以达到更好的效果。

Conclusion

本文定义了一种统一的基于词信息量的方法，来定量解释NLP深度神经模型的中间层。与现有方法相比，基于词信息量的方法可以跨时间戳、图层和模型（一贯性）提供一致且忠实的结果。 而且，它可以用最小化假设（普适性）来定义，适用与各个模型结构和任务。 最后，实验展示了如何将基于词信息的度量用作解释模型的工具，并展示了如何丰富理解DNN的能力。

如有错误，欢迎讨论和指出，万分感谢。

References

[1]. 神经网络的可解释性，从经验主义到数学建模(一篇icml文)
[2]. Towards a Deep and Unified Understanding of Deep Neural Models in NLP
[3]. Kinney, J. B. and Atwal, G. S. Equitability, mutual information, and the maximal information coefficient. National Academy of Sciences, pp. 201309933, 2014.