automl-超参数优化（HPO）-综述

一、概述

超参数优化的意义

目前人工智能和深度学习越趋普及，大家可以使用开源的Scikit-learn、TensorFlow来实现机器学习模型，甚至参加Kaggle这样的建模比赛。那么要想模型效果好，手动调参少不了，机器学习算法如SVM就有gamma、kernel、ceof等超参数要调，而神经网络模型有learning_rate、optimizer、L1/L2 normalization等更多超参数可以调优。

很多paper使用一个新的模型可以取得state of the art的效果，然后提供一组超参数组合方便读者复现效果，实际上这些超参数都是“精挑细选”得到的，背后有太多效果不好的超参数尝试过程被忽略，大家也不知道对方的超参数是如何tune出来的。因此，了解和掌握更好的超参数调优方法在科研和工程上是很有价值的。

超参数简介

首先，什么是超参数（Hyper-parameter）？超参数其实是相对于模型的参数而言（Parameter）。

• 我们知道机器学习其实就是通过某种算法学习数据的计算过程，在训练过程中能够被调整的那部分参数被称为模型的参数。例如：全连接矩阵中的各个数值就属于模型参数。

• 还有一部分参数在训练之前就必须定义，而在训练过程中不能被调整。例如：模型的属性、控制训练过程的属性，我们称为超参数。例如我们定义一个神经网络模型有9527层网络并且都用RELU作为激活函数，这个9527层和RELU激活函数就是一组超参数，又例如我们定义这个模型使用RMSProp优化算法和learning rate为0.01，那么这两个控制训练过程的属性也是超参数。

显然，超参数的选择对模型最终的效果有极大的影响。如复杂的模型可能有更好的表达能力来处理不同类别的数据，但也可能因为层数太多导致梯度消失无法训练，又如learning rate过大可能导致收敛效果差，过小又可能收敛速度过慢。

那么如何选择合适的超参数呢，不同模型会有不同的最优超参数组合，找到这组最优超参数大家会根据经验、或者随机的方法来尝试，这也是为什么现在的深度学习工程师也被戏称为“调参工程师”。
不存在一组完美的超参数适合所有模型，那么调参看起来是一个工程问题。**有可能用数学或者机器学习模型来解决模型本身超参数的选择问题吗？**答案显然是有的，而且通过一些数学证明，我们使用算法“很有可能”取得比常用方法更好的效果，为什么是“很有可能”，因为这里没有绝对只有概率分布，也就是后面会介绍到的贝叶斯优化。

超参数优化问题的前提假设(基本特征)

1、机器学习模型超参数调优一般认为是一个黑盒优化问题，所谓黑盒问题就是我们在调优的过程中只看到模型的输入和输出，不能获取模型训练过程的梯度信息，也不能假设模型超参数和最终指标符合凸优化条件，否则的话我们通过求导或者凸优化方法就可以求导最优解，不需要使用这些黑盒优化算法。而实际上大部分的模型超参数也符合黑盒优化这个假设。

2、模型的训练过程是相对expensive的，不能通过快速计算获取大量样本。（直接用强化学习是不可取的）
强化学习每一个action操作后都能迅速取得当前的score，这样收集到大量样本才可以训练复杂的神经网络模型，那能否直接用强化学习来进行超参数优化？
虽说我们也可以用增强学习来训练超参数调优的模型，但实际上一组超参数要训练一个模型需要几分钟、几小时、几天甚至几个月的时间，无法快速获取这么多样本数据（反馈结果），因此需要有更“准确和高效”的方法来调优超参数。

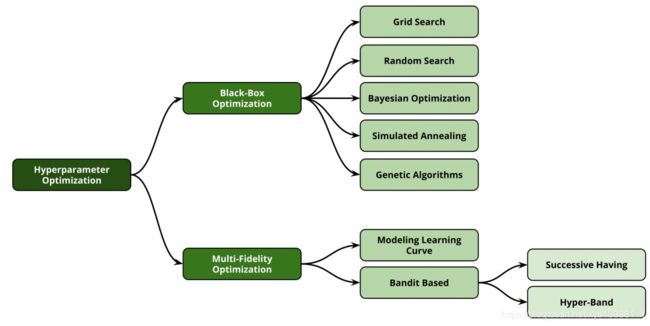
超参数优化方法分类：

超参数优化方法分类（model-free和model-based都属于黑盒优化）

超参数优化的难题

• 当面对大模型、大数据集、复杂的机器学习时，功能函数的评估非常昂贵
• 配置空间非常复杂且是高维的
• 我们通常不能得到关于超参数的损失函数的梯度。此外，在经典优化中经常使用的目标函数的其他特性通常不适用，如凸性和平滑性。

二、问题描述

A为机器算法，该算法具有N个超参数；
第n个超参数的域为Yn，则全部超参数的配置空间为Y=Y1 x Y2 … x Yn；
用λ表示超参数的矢量，Aλ表示带有参数实例的机器算法。

给定数据集Dtrain和Dvalid，目标为

Alternatives to Optimization: Ensembling and Marginalization（优化的替代方案：集成和边缘化）

除了在这些操作符上使用argmin-operator之外，还可以构造一个集成(目的是最小化给定验证协议的损失)或集成所有超参数(如果考虑的模型是一个概率模型)。
当HPO识别出许多好的配置时，仅选择单个超参数配置可能是浪费，将它们组合成一个集成可以提高性能[109]。这在具有较大配置空间的自动化系统(例如，在FMS或CASH中)中特别有用，在这些系统中，良好的配置可以非常多样化，这增加了集成的潜在收益。
到目前为止讨论的方法在HPO程序之后应用集成。虽然它们在实践中提高了性能，但基本模型并没有针对集成进行优化。但是，也可以直接对模型进行优化，从而最大程度地改进现有的集成
在处理贝叶斯模型时，通常可以整合出机器学习算法的超参数。

多目标优化

有时候需要考虑多个目标，如性能和计算资源，或者由多个损失函数。
两种解决办法：
1、如果已知二级性能度量的限制(例如最大内存消耗)，则可以将该问题表述为约束优化问题。
2、更通用的办法：寻找帕累托前沿。

三、常用的黑盒优化方法

通常来说，任何黑盒优化方法都可用于超参数优化。
由于问题的非凸性，全局优化算法通常是首选的，但优化过程中的一些局部性是有用的。

Grid search

网格搜索很容易理解和实现，例如我们的超参数A有2种选择，超参数B有3种选择，超参数C有5种选择，那么我们所有的超参数组合就有2 * 3 * 5也就是30种，我们需要遍历这30种组合并且找到其中最优的方案，对于连续值我们还需要等间距采样。
实际上这30种组合不一定取得全局最优解，而且计算量很大很容易组合爆炸，并不是一种高效的参数调优方法。

Random search

1、参数很多时，网格搜索太费时
但是当超参数个数比较多的时候，我们仍然采用网格搜索，那么搜索所需时间将会指数级上升。
比如我们有四个超参数，每个范围都是[10,100]，那么我们所需的搜索次数是101010*10=10^4。
如果再增加一个超参数，那么所需的搜索次数是10^5，搜索时间指数级上升。
所以很多很多个超参数的情况，假如我们仍然采用网格搜索不现实。

2、 网格稀疏化并不好
所以出现了这样的做法，将网格取稀疏一点，比如上面例子中的[10,100]，我们就去10,30,50,70,90这几个数，降低一下搜索次数。
这样变快了一点，但是有可能找到的超参数不是全局最小。

3、随机搜索
所以又有人提出了随机搜索的方法，随机在超参数空间中搜索几十几百个点，其中就有可能会有比较小的值。
这种做法比上面稀疏化网格的做法快，而且实验证明，随机搜索法结果比稀疏化网格法稍好。

随机搜索的思想和网格搜索比较相似，只是不再测试上界和下界之间的所有值，只是在搜索范围中随机取样本点。它的理论依据是，如果随即样本点集足够大，那么也可以找到全局的最大或最小值，或它们的近似值。通过对搜索范围的随机取样，随机搜索一般会比网格搜索要快一些。但是和网格搜索的快速版（非自动版）相似，结果也是没法保证的。

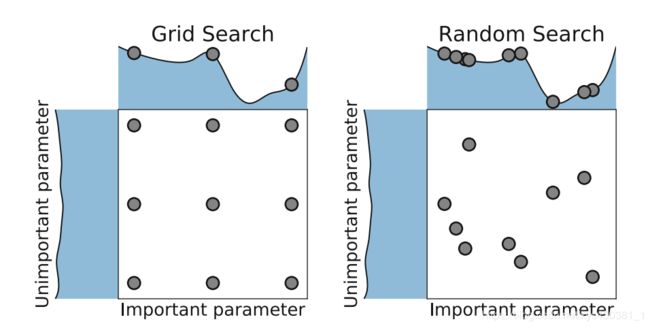
业界公认的Random search效果会比Grid search好。

随机优于网格搜索的地方：

• This works better than grid search when some hyperparameters are much more important than others (a property that holds in many cases （没看明白）

• 在网格布局中，很容易注意到，即使已经训练了9个模型，而每个变量只使用了3个值。然而，使用随机搜索，我们不太可能不止一次地选择相同的变量，将使用9个不同的值为每个变量训练9个模型。

Bayesian Optimization

参考另一篇文章：超参数优—贝叶斯优化及其改进（PBT优化）

群体优化算法（进化算法、PSO）

像遗传算法和PSO这些经典黑盒优化算法，我归类为群体优化算法，也不是特别适合模型超参数调优场景，因为需要有足够多的初始样本点，并且优化效率不是特别高，本文也不再详细叙述。
优点：并行化

多保真度优化

数据集越来越大、机器学习模型越来越复杂—>黑盒优化的性能评估非常昂贵。

解决办法：
数据集子集
训练轮数减少
特征降维
…

多保真度方法：将上述启发式方法改为形式化算法，通过降低保真度的评估算法来近似真实的评估值

Learning Curve-Based Prediction for Early Stopping

学习曲线外推法用于预测终止。
使用一个学习曲线模型来对一个部分观察的学习曲线进行推测，如果在优化过程中预测该曲线在以后都不可能超过到目前为止所训练的最佳模型的性能，则停止训练过程。
papers：

• Speeding up automatic hyperparameter optimization of deep neural networks by extrapolation of learning curves
• Freeze-thaw Bayesian optimization（早停+贝叶斯优化）
• LEARNING CURVE PREDICTION WITH BAYESIAN NEURAL NETWORKS (ICLR2018)

Bandit-Based Algorithm Selection Methods

目的：如何从一个算法集合中选择最好的算法（从参数集合中选择最好的参数）。
什么是bandit算法？
multi-armed bandit是非常经典的序列决策模型，要解决的问题是平衡“探索”(exploration)和“利用”(exploitation)。
举一个bandit例子，你有20个按钮，每个按钮按一次可能得到一块钱或者拿不到钱，同时每个按钮的得到一块钱的概率不同，而你在事前对这些概率一无所知。在你有1000次按按钮的机会下，如何得到最大收益。
这类算法，通过将自动调参问题，转化为bandit问题，配置更多资源给表现更优异的参数模型。

Bandit算法来源于历史悠久的赌博学，它要解决的问题是这样的：
一个赌徒，要去摇老虎机，走进赌场一看，一排老虎机，外表一模一样，但是每个老虎机吐钱的概率可不一样，他不知道每个老虎机吐钱的概率分布是什么，那么每次该选择哪个老虎机可以做到最大化收益呢？这就是多臂赌博机问题（Multi-armed bandit problem, K-armed bandit problem, MAB）。
怎么解决这个问题呢？最好的办法是去试一试，不是盲目地试，而是有策略地快速试一试，这些策略就是Bandit算法。

bandit问题与推荐系统
这个多臂问题，推荐系统里很多问题都与它类似：

• 假设一个用户对不同类别的内容感兴趣程度不同，那么我们的推荐系统初次见到这个用户时，怎么快速-地知道他对每类内容的感兴趣程度？这就是推荐系统的冷启动。
• 假设我们有若干广告库存，怎么知道该给每个用户展示哪个广告，从而获得最大的点击收益？是每次都挑效果最好那个么？那么新广告如何才有出头之日？
• 我们的算法工程师又想出了新的模型，有没有比A/B test更快的方法知道它和旧模型相比谁更靠谱？
• 如果只是推荐已知的用户感兴趣的物品，如何才能科学地冒险给他推荐一些新鲜的物品？

连续减半法：
Non-stochastic Best Arm Identification and Hyperparameter Optimization

HyperBand
Hyperband: A novel bandit-based approach to hyperparameter optimization
网络博文：机器学习超参数优化算法-Hyperband

1、贝叶斯优化的缺点：

• 对于那些具有未知平滑度和有噪声的高维、非凸函数，BO算法往往很难对其进行拟合和优化，而且通常BO算法都有很强的假设条件，而这些条件一般又很难满足。
• 为了解决上面的缺点，有的BO算法结合了启发式算法(heuristics)，但是这些方法很难做到并行化

2、hyperband要做什么？
为了解决贝叶斯的上述问题，Hyperband算法被提出。在介绍Hyperband之前我们需要理解怎样的超参数优化算法才算是好的算法，如果说只是为了找到最优的超参数组合而不考虑其他的因素，那么我们那可以用穷举法，把所有超参数组合都尝试一遍，这样肯定能找到最优的。但是我们都知道这样肯定不行，因为我们还需要考虑时间，计算资源等因素。而这些因素我们可以称为Budget,用B表示。

• 优化过程中需要考虑时间计算资源等因素。而这些因素我们可以称为Budget,用B表示。
• 假设一开始候选的超参数组合数量是n，那么分配到每个超参数组的预算就是B/n。
• 所以Hyperband做的事情就是在n与B/n做权衡(tradeoff)。解释如下：
  • 我们希望候选的超参数越多越好，因为这样能够包含最优超参数的可能性也就越大，但是此时分配到每个超参数组的预算也就越少，评估就不准确了，进而找到最优超参数的可能性就降低了。反之亦然。这是一组矛盾！
  • 而Hyperband要做的事情就是既要预设尽可能多的超参数组合数量，又要给每组超参数（或者其中较优秀的参数配置）分配尽可能多的预算，从而确保尽可能地找到最优超参数。

3、hyperband算法
Hyperband算法对 Jamieson & Talwlkar(2015)提出的SuccessiveHalving算法做了扩展。所以首先介绍一下SuccessiveHalving算法是什么。
其实仔细分析SuccessiveHalving算法的名字你就能大致猜出它的方法了：假设有n组超参数组合，然后对这n组超参数均匀地分配预算并进行验证评估，根据验证结果淘汰一半表现差的超参数组，然后重复迭代上述过程直到找到最终的一个最优超参数组合。

基于这个算法思路，如下是Hyperband算法步骤：

注意上述算法中对超参数设置采样使用的是均匀随机采样，所以有算法在此基础上结合贝叶斯进行采样，
提出了BOHB:Practical Hyperparameter Optimization for Deep Learning

4、hyperband实例
总体思路我们由一个自动调节LeNet的例子来展示：
文中给出了一个基于MNIST数据集的示例，并将迭代次数定义为预算(Budget),即一个epoch代表一个预算。超参数搜索空间包括学习率，batch size,kernel数量等。

令R=81,η=3，所以smax=4, 总预算B=5R=5×81。

下图给出了需要训练的超参数组和数量和每组超参数资源分配情况。

由算法可以知道有两个loop，其中inner loop表示SuccessiveHalving算法。再结合下图左边的表格，每次的inner loop，用于评估的超参数组合数量越来越少，与此同时单个超参数组合能分配的预算也逐渐增加，所以这个过程能更快地找到合适的超参数。

右边的图给出了不同s对搜索结果的影响，可以看到s=0或者s=4并不是最好的，所以并不是说s越大越好。

资源分配表：每一列代表一个外循环，外循环占用的总资源就是B=5R=5x81。ni代表第i个内循环的参数组合，ri代表第i个内循环中每组参数占用的资源。
表中可以看出：

• 从一列的不同行进行比较：早期，尽量多地探索新的配置，但每个配置只稍微试一下就停止；后期，逐渐聚焦到好的参数配置上；后期的配置是从前期的配置中优选出来的。如果一个配置坚持到最后一行还被保留，则它已经经过了前面的r0+r1+…+ri次训练和评估比较，即使不是最优，但通常也不会差到哪里去了。
• 从不同列来比较：不同列的初始配置集合是不一样的，不同列探索的最大配置数目（最大的ni）是不一样的。不同的列代表了不同的n与B/n的"tradeoff"

参考文献

网络博文

贝叶斯优化: 一种更好的超参数调优方式
[机器学习]超参数优化—贝叶斯优化(Bayesian Optimization) 理解
为什么贝叶斯优化比网格搜索和随机搜索更高效呢？

论文

黑盒优化
网格随机搜索

• 2017 | Design and analysis of experiments. | Montgomery | PDF
• 2015 | Adaptive control processes: a guided tour. | Bellman | PDF
• 2012 | Random search for hyper-parameter optimization. | Bergstra and Bengio | JMLR | PDF

贝叶斯优化

• 2018 | Bohb: Robust and efficient hyperparameter optimization at scale. | Falkner et al. | JMLR | PDF
• 2017 | On the state of the art of evaluation in neural language models. | Melis et al. | PDF
• 2015 | Automating model search for large scale machine learning. | Sparks et al. | ACM-SCC | PDF
• 2015 | Scalable bayesian optimization using deep neural networks. | Snoek et al. | ICML | PDF
• 2014 | Bayesopt: A bayesian optimization library for nonlinear optimization, experimental design and bandits. | Martinez-Cantin | JMLR | PDF
• 2013 | Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. | Bergstra et al. | PDF
• 2013 | Towards an empirical foundation for assessing bayesian optimization of hyperparameters. | Eggensperger et al. | NIPS | PDF
• 2013 | Improving deep neural networks for LVCSR using rectified linear units and dropout. | Dahl et al. | IEEE-ICASSP | PDF
• 2012 | Practical bayesian optimization of machine learning algorithms. | Snoek et al. | NIPS | PDF—（Spearmint算法，高斯过程回归）
• 2011 | Sequential model-based optimization for general algorithm configuration. | Hutter et al. | LION | PDF—（SMBO,SMAC，随机森林，可用于连续、离散、categorical选项）
• 2011 | Algorithms for hyper-parameter optimization. | Bergstra et al. | NIPS | PDF—（TPE，树状结构优化，可用于连续、离散、categorical选项）
  论文解读：Algorithms for Hyper-Parameter Optimization
• 1998 | Efficient global optimization of expensive black-box functions. | Jones et al. | PDF
• 1978 | Adaptive control processes: a guided tour. | Mockus et al. | PDF
• 1975 | Single-step Bayesian search method for an extremum of functions of a single variable. | Zhilinskas | PDF
• 1964 | A new method of locating the maximum point of an arbitrary multipeak curve in the presence of noise. | Kushner | PDF

模拟退火

• 1983 | Optimization by simulated annealing. | Kirkpatrick et al. | Science | PDF

一般算法

• 1992 | Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. | Holland et al. | PDF

多精度优化

• 2019 | Multi-Fidelity Automatic Hyper-Parameter Tuning via Transfer Series Expansion. | Hu et al. | PDF
• 2016 | Review of multi-fidelity models. | Fernandez-Godino | PDF
• 2012 | Provably convergent multifidelity optimization algorithm not requiring high-fidelity derivatives. | March and Willcox | AIAA | PDF

建模学习曲线

• 2015 | Speeding up automatic hyperparameter optimization of deep neural networks by extrapolation of learning curves. | Domhan et al. | IJCAI | PDF
• 1998 | Efficient global optimization of expensive black-box functions. | Jones et al. | JGO | PDF

强盗算法 bandit-based

• 2016 | Non-stochastic Best Arm Identification and Hyperparameter Optimization. | Jamieson and Talwalkar | AISTATS | PDF
• 2018 | Hyperband: A novel bandit-based approach to hyperparameter optimization 第四版. | Kirkpatrick et al. | JMLR | PDF
• Bohb: Robust and efficient hyperparameter optimization at scale 将贝叶斯优化与hyperband相结合