图神经网络GNN 原理 详解 (一)
图神经网络(GNN)
一.背景
图神经网络的概念首先由 Gori 等人(2005)[16] 提出,并由 Scarselli 等人(2009)[17] 进一步阐明。这些早期的研究以迭代的方式通过循环神经架构传播邻近信息来学习目标节点的表示,直到达到稳定的固定点。该过程所需计算量庞大,而近来也有许多研究致力于解决这个难题。在本文中,图神经网络代表的是所有用于图数据的深度学习方法。

受到卷积网络在计算机视觉领域所获巨大成功的激励,近来出现了很多为图数据重新定义卷积概念的方法。这些方法属于图卷积网络(GCN)的范畴。Bruna 等人(2013)提出了关于图卷积网络的第一项重要研究,他们基于谱图论(spectral graph theory)开发了一种图卷积的变体。自此,基于谱的图卷积网络不断改进、拓展、进阶。由于谱方法通常同时处理整个图,并且难以并行或扩展到大图上,基于空间的图卷积网络开始快速发展
二.图的概念和基础
2.1 图论介绍
图论〔Graph Theory〕是数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。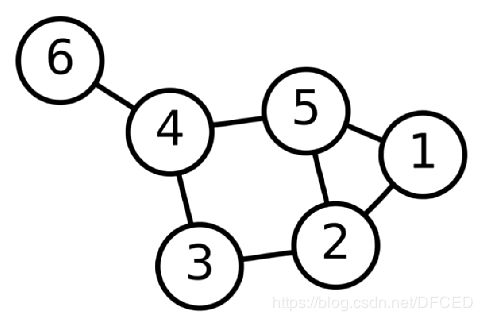
世界中很多的信息之间的联系,都可以使用图这种抽象的数学方式来进行表示,如下就是表示互联网之间关系的连接图。

2.2 图论基本研究对象-----图
图(Graph)是表示物件与物件之间的关系的数学对象,是图论的基本研究对象。一个不带权图中若两点不相邻,邻接矩阵相应位置为0,对带权图(网),相应位置为∞。
对于一个拥有n个顶点的无向连通图,它的边数一定多于n-1条。若从中选择n-1条边,使得无向图仍然连通,则由n个顶点及这 n-1条边(弧)组成的图被称为原无向图的生成树。
2.3 图的定义
二元组的定义
图G是一个有序二元组(V,E),其中V称为顶集(Vertices Set),E称为边集(Edges set),E与V不相交。它们亦可写成V(G)和E(G)。
E的元素都是二元组,用(x,y)表示,其中x,y∈V。
三元组的定义
图G是指一个三元组(V,E,I),其中V称为顶集,E称为边集,E与V不相交;I称为关联函数,I将E中的每一个元素映射到![]() 。如果e被映射到(u,v),那么称边e连接顶点u,v,而u,v则称作e的端点,u,v此时关于e相邻。同时,若两条边i,j有一个公共顶点u,则称i,j关于u相邻。
。如果e被映射到(u,v),那么称边e连接顶点u,v,而u,v则称作e的端点,u,v此时关于e相邻。同时,若两条边i,j有一个公共顶点u,则称i,j关于u相邻。
2.4 分类
有/无向图
如果给图的每条边规定一个方向,那么得到的图称为有向图。在有向图中,与一个节点相关联的边有出边和入边之分。相反,边没有方向的图称为无向图。
单图
一个图如果任意两顶点之间只有一条边(在有向图中为两顶点之间每个方向只有一条边);边集中不含环,则称为单图。
三.GNN(基于循环结构) 的理论基础------不懂点理论
要想搞懂GNN,那就必须知道什么是不动点理论。
GNN的理论基础是不动点(the fixed point)理论,这里的不动点理论专指巴拿赫不动点定理(Banach’s Fixed Point Theorem)。
3.1 巴拿赫不动点定理
定义
巴拿赫不动点定理,又称为压缩映射定理或压缩映射原理,是度量空间理论的一个重要工具。它保证了度量空间的一定自映射的不动点的存在性和唯一性,并提供了求出这些不动点的构造性方法。这个定理是以斯特凡·巴拿赫命名的,他在1922年提出了这个定理。
定理内容
设(X,d)为非空的完备度量空间。设T:X→X为X上的一个压缩映射,也就是说,存在一个非负的实数q<1,使得对于所有X内的x和y,都有: ![]()
那么映射T在X内有且只有一个不动点x(这就是说,Tx=x)。更进一步,这个不动点可以用以下的方法来求出:从X内的任意一个元素x0开始,并定义一个迭代序列xn=Txn-1,对于n= 1,2,3,……。这个序列收敛,且极限为x。以下的不等式描述了收敛的速率:
![]()
等价地:
![]()
且
![]()
满足以上不等式的最小的q有时称为利普希茨常数。
注意对于所有不同的x和y都有d(Tx,Ty) < d(x,y)的要求,一般来说是不足以保证不动点的存在的,例如映射T: [1,∞) → [1,∞),T(x) =x+ 1/x,就没有不动点。但是,如果空间X是紧的,则这个较弱的假设也能保证不动点的存在。
当实际应用这个定理时,最艰难的部分通常是恰当地定义X,使得T实际上把元素从X映射到X,也就是说,Tx总是X的一个元素。
在GNN中的操作
首先我们用 F 表示若干个 f 堆叠得到的一个函数,也称为全局更新函数,那么图上所有结点的状态更新公式可以写成:
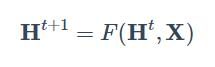
不动点定理指的就是,不论![]() 是什么,只要 F 是个压缩映射(contraction map),
是什么,只要 F 是个压缩映射(contraction map),![]() 经过不断迭代都会收敛到某一个固定的点,我们称之为不动点。
经过不断迭代都会收敛到某一个固定的点,我们称之为不动点。
3.2 什么是压缩映射?
定义
设(X, ρ)为距离空间,T是X 到 X中的映射,如果存在数a (0 那么既然 f 是由 神经网络实现的,如何保证它是一个压缩映射呢? 一种实现方法可以是把每个邻居结点的特征、隐藏状态、每条相连边的特征以及结点本身的特征简单拼接在一起,在经过前馈神经网络后做一次简单的加和。 从将图输入到GNN中到得到输出结果 主要可以分为两步:第一步是传播(propagation)过程,即节点表示随时间的更新过程;第二步是输出(output)过程,即根据最终的节点表示得到目标输出(如每个节点的类别)的过程。在这两步中,传播过程要更为重要,其设计也要受到一定的约束(要保证整个图上的状态映射是一个压缩映射(contraction map))。在展开图中,传播过程对应于从 GNN的学习是通过Almeida-Pineda算法实现的。该算法的特点在于,首先通过传播过程使整个图收敛,然后在收敛解上计算相应的梯度。这样,我们就无需存储梯度计算过程所需的中间状态了。但是,必须保证整个图的映射是压缩的,以保证传播过程有一个收敛解。 实验结果表明GNN对于结构化数据的建模十分有效,但仍然存在着诸多的不足。3.3 用前馈神经网络实现 压缩映射
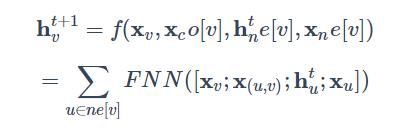
那我们如何保证 f 是个压缩映射呢,其实是通过限制 f 对 H 的偏导数矩阵的的惩罚项大小,这是通过一个对雅可比矩阵(Jacobian Matrix)的惩罚项(Penalty)来实现的。什么是雅克比矩阵?
四.GNN的训练流程
3.1 流程 步骤
![]() 到
到 ![]() 的更新过程(注意,
的更新过程(注意, ![]() 并不是确定的,而是对应于整个图的状态到达不动点的时刻),不同时间步的连接则由图中的连接来决定(可以是有向的,也可以是无向的)。
并不是确定的,而是对应于整个图的状态到达不动点的时刻),不同时间步的连接则由图中的连接来决定(可以是有向的,也可以是无向的)。传播过程
输出过程
GNN 的训练

五. GNN 的 不足




