数字图像处理笔记（五）：直方图均衡与直方图匹配（规定化）

1 - 直方图处理

直方图是多种空间域处理技术的基础，可以用于图像增强。

2 - 直方图均衡

考虑连续灰度值，并用变量r表示待处理图像的灰度。设r的取值区间为[0,L-1],且r = 0表示黑色，r = L - 1表示白色。令$p_r(r)$和$p_s(s)$分别表示随机变量r和s的概率密度函数，概率密度函数归一化后可以画出图像的直方图

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt

image = cv.imread('images/test_1.jpg', 0)
hist = cv.calcHist([image],[0],None,[256],[0,255])
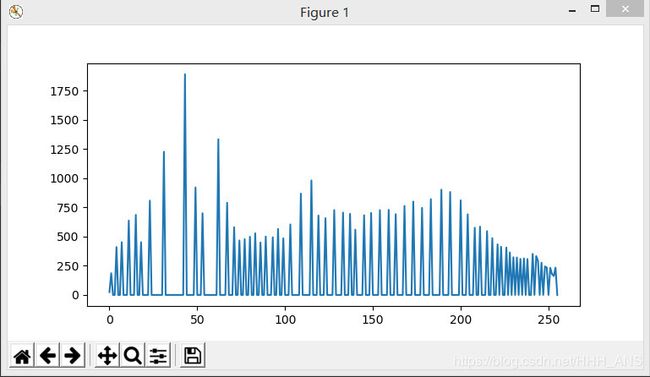
plt.plot(hist)
plt.show()

可以看到较暗的图片灰度直方图分布的非常不均衡，那么我们构造一个出变换
$$s=T(r)=(L-1){\int }_0^r{p}_r(w)dw,0\le r\le L-1$$
使得对应的输出图像概率密度函数变成均匀的

对于离散值，我们处理其概率（直方图值）与求和来替代处理概率密度函数与积分。
一副数字图像中灰度级$r_k$出现的概率近似为：
$$p_r(r_k)=\frac{n_k}{MN},k=0,1,2,\dots ,L-1$$
其中，MN是图像中像素的综述，$n_k$是灰度为$r_k$像素的个数。
则离散形式的变化公式为：
$$s_k=T(r_k)=(L-1)\sum _{j=0}^k{p}_r(r_j)=\frac{(L-1)}{MN}\sum _{j=0}^k{n}_j,k=0,1,2,\dots ,L-1$$

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt

image = cv.imread('images/test_1.jpg', 0)
image2 = cv.equalizeHist(image)
cv.imshow("image_2",image2)
hist = cv.calcHist([image2],[0],None,[256],[0,255])
plt.plot(hist)
plt.show()
cv.waitKey(0)

可以看到直方图的分布更加均匀了，图像的对比度和相关细节显示的也更加明显了。

3 - 直方图匹配

直方图均衡能自动地确定变换函数，当需要自动增强时，这是一种好方法，因为由于这种技术得到的结果可以预知，并且这种方法实现也很简单，但是对于某些应用，采用均匀直方图的基本增强并不是最好的方法，有时我们希望处理后的图像具有规定的直方图形状可能更有用。这种采用处理后有特殊直方图的方法称为直方图匹配或直方图规定划。

例：直方图规定划
设一副图片的灰度概率密度函数（PDF）为$p_r(r)=2r/(L-1{)}^2,0\le r\le (L-1)$

我们想要寻找一个变换函数，使得产生的图像的灰度PDF是$p_z(z)=3z^2/(L-1{)}^3,0\le r\le (L-1)$

求出原图像的直方图均衡变换：
$$s=T(r)=(L-1){\int }_0^r{p}_r(w)dw=\frac{2}{(L-1)}{\int }_o^{r}wdw=\frac{r^2}{(L-1)},0\le r\le L-1$$

求出规定图像的直方图均衡变换：
$$G(z)=(L-1){\int }_0^z{p}_z(w)dw=\frac{3}{(L-1{)}^2}{\int }_o^z{w}^{2}dw=\frac{z^3}{(L-1{)}^2},0\le r\le L-1$$

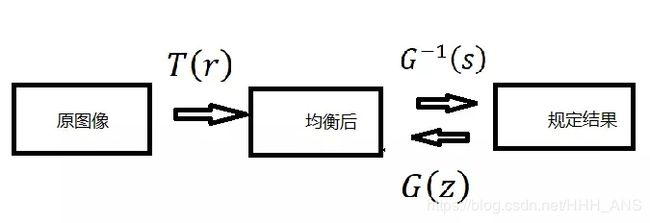
最后使其相等$G(z)=s$

利用反变换得到$z=G^{-}1[T(r)]=G^{-}1(s)$

画出函数的关系图就很好理解了

在离散形式下
$$s_k=T(r_k)=(L-1)\sum _{j=0}^k{p}_r(r_j)=\frac{(L-1)}{MN}\sum _{j=0}^k{n}_j,k=0,1,2,\dots ,L-1$$
$$G(z_q)=(L-1)\sum _{i=0}^q{p}_z(z_i)$$
对于一个q值，有$G(z_q)=s_k$
再利用反变换，有$Z_q=G^{-}1(s_k)$

那么我们总结直方图规定划过程如下：

1. 计算给定图像的直方图$p_r(r)$，并用它寻找直方图均衡变换，把$s_k$四舍五入为范围[0,L-1]内的整数。
2. 计算变换函数G的所有值，将G的值储存在一个表中
3. 对于每个值，使用储存的G值寻找相应的$z_Q$值，使$G（z_q）$最接近$s_k$。
4. 首先对输入图像进行均衡，然后使用步骤3找到的映射把该图像中的每个均衡后的像素值$s_k$映射为直方图规定划后的图像相应$z_q$值

具体python实现：
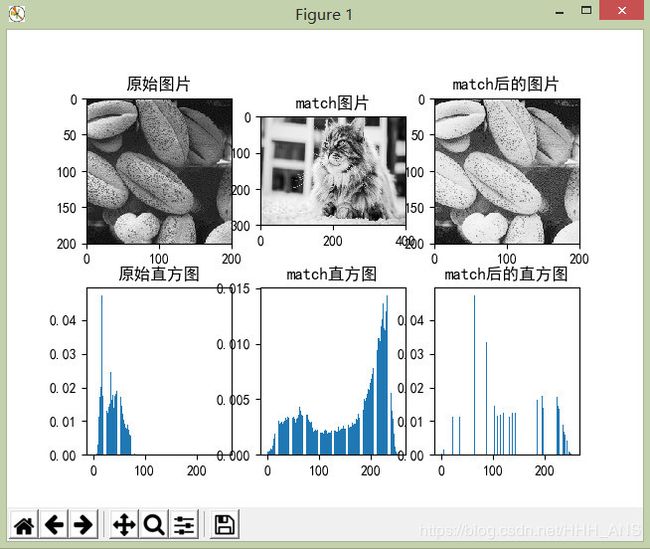
将一张较为黑暗的原始图像
与一张拍摄光线较好的匹配图像
进行直方图匹配，目的是为了把原始图像的直方图匹配成匹配图像的直方图分布，使得原始图像能够呈现出匹配图像的光线效果。

import numpy as np
from matplotlib import pyplot as plt
from PIL import Image
import matplotlib


matplotlib.rcParams['font.sans-serif']=['SimHei']   # 用黑体显示中文

#传入的直方图要求是个字典，每个灰度对应着概率
def drawHist(hist,name):
    keys = hist.keys()
    values = hist.values()
    x_size = len(hist)-1#x轴长度，也就是灰度级别
    axis_params = []
    axis_params.append(0)
    axis_params.append(x_size)

    #plt.figure()
    if name != None:
        plt.title(name)
    plt.bar(tuple(keys),tuple(values))#绘制直方图
    #plt.show()

#将灰度数组映射为直方图字典,nums表示灰度的数量级
def arrayToHist(grayArray,nums):
    if(len(grayArray.shape) != 2):
        print("length error")
        return None
    w,h = grayArray.shape
    hist = {}
    for k in range(nums):
        hist[k] = 0
    for i in range(w):
        for j in range(h):
            if(hist.get(grayArray[i][j]) is None):
                hist[grayArray[i][j]] = 0
            hist[grayArray[i][j]] += 1
    #normalize
    n = w*h
    for key in hist.keys():
        hist[key] = float(hist[key])/n
    return hist
#计算累计直方图计算出新的均衡化的图片，nums为灰度数,256
def equalization(grayArray,h_s,nums):
    #计算累计直方图
    tmp = 0.0
    h_acc = h_s.copy()
    for i in range(256):
        tmp += h_s[i]
        h_acc[i] = tmp

    if(len(grayArray.shape) != 2):
        print("length error")
        return None
    w,h = grayArray.shape
    des = np.zeros((w,h),dtype = np.uint8)
    for i in range(w):
        for j in range(h):
            des[i][j] = int((nums - 1)* h_acc[grayArray[i][j] ] +0.5)
    return des

def histMatch(grayArray,h_d):
    #计算累计直方图
    tmp = 0.0
    h_acc = h_d.copy()
    for i in range(256):
        tmp += h_d[i]
        h_acc[i] = tmp

    h1 = arrayToHist(grayArray,256)
    tmp = 0.0
    h1_acc = h1.copy()
    for i in range(256):
        tmp += h1[i]
        h1_acc[i] = tmp
    #计算映射
    M = np.zeros(256)
    for i in range(256):
        idx = 0
        minv = 1
        for j in h_acc:
            if (np.fabs(h_acc[j] - h1_acc[i]) < minv):
                minv = np.fabs(h_acc[j] - h1_acc[i])
                idx = int(j)
        M[i] = idx
    des = M[grayArray]
    return des

imdir = "images/test_1.jpg"#原始图片的路径
imdir_match = "images/persian_cat.jpg"

#直方图匹配
#打开文件并灰度化
im_s = Image.open(imdir).convert("L")
im_s = np.array(im_s)
print(np.shape(im_s))
#打开文件并灰度化
im_match = Image.open(imdir_match).convert("L")
im_match = np.array(im_match)
print(np.shape(im_match))
#开始绘图
plt.figure()

#原始图和直方图
plt.subplot(2,3,1)
plt.title("原始图片")
plt.imshow(im_s,cmap='gray')

plt.subplot(2,3,4)
hist_s = arrayToHist(im_s,256)
drawHist(hist_s,"原始直方图")

#match图和其直方图
plt.subplot(2,3,2)
plt.title("match图片")
plt.imshow(im_match,cmap='gray')

plt.subplot(2,3,5)
hist_m = arrayToHist(im_match,256)
drawHist(hist_m,"match直方图")

#match后的图片及其直方图
im_d = histMatch(im_s,hist_m)#将目标图的直方图用于给原图做均衡，也就实现了match
plt.subplot(2,3,3)
plt.title("match后的图片")
plt.imshow(im_d,cmap='gray')

plt.subplot(2,3,6)
hist_d = arrayToHist(im_d,256)
drawHist(hist_d,"match后的直方图")

plt.show()

实验结果：