hdu 3830 Checkers 【非常好的思维题】
文章目录
- 题目链接:
题目链接:
http://acm.hdu.edu.cn/showproblem.php?pid=3830
题意:坐标上给三个点 ( x 1 , y 1 , z 1 ) (x_1,y_1,z_1) (x1,y1,z1),问能不能移动成另外3个点 ( x 2 , y 2 , z 2 ) (x_2,y_2,z_2) (x2,y2,z2)
移动的规则是:
比如 ( x , y , z ) (x,y,z) (x,y,z),设 t 1 = y − x , t 2 = z − y t_1=y-x,t_2=z-y t1=y−x,t2=z−y
中间的点 y y y只能变成 ( x − t 1 , y − t 1 , z ) (x-t_1,y-t_1,z) (x−t1,y−t1,z)或 ( x , y + t 1 , z + t 1 ) (x,y+t_1,z+t_1) (x,y+t1,z+t1)
x向右移动只能变成 ( y , x + t 1 + t 1 , z ) (y,x+t_1+t_1,z) (y,x+t1+t1,z)
z向左移动只能变成 ( x , z − t 2 − t 2 , y ) (x,z-t_2-t_2,y) (x,z−t2−t2,y)
初步分析一波我们阔以发现
如果 t 1 t_1 t1的长度小于 t 2 t_2 t2,那就只能 x x x移动
如果 t 2 t_2 t2的长度小于 t 1 t_1 t1,那就只能 z z z移动
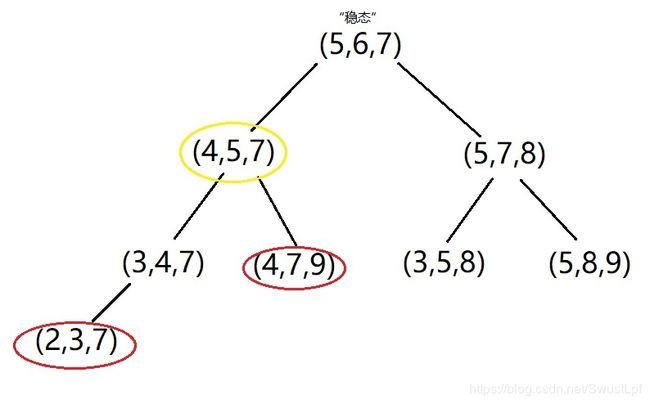
那么这个区间就会越来越小,最后达到 t 1 = t 2 t_1=t_2 t1=t2的“稳态”的情况
那我们就阔以找到两个的稳态,看他们相不相同,
不相同那肯定不行
相同的话那就记录到大稳态要走的步数,然后两个相加,不就行了嘛~
以为理论上AC了,但是,万一他们在同一边,那就需要相减了啊,那怎么知道是加还是减呢?
理论AC失败T_T
后来发现,其实是这个关系
就是要求红色的两个点,最短路径很明显,就是经过lca的这段路径
但是我们不可能像图论那样去求,因为点非常多
但是有个东西我们是知道的,每个点到“稳态”点走的步数是阔以计算出来的,于是就向上走,看走到什么时候,两个点一样了,就走到lca了,但是一步一步走肯定是要超时的,于是就想到二分了(我想不到)
走到的点不同,就继续走,走到的点相同,是不是走过了喃?满足二分的性质
二分没学好,直接以为mid就是lca到“稳态”的距离,应该判断成功后才记录一次答案
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int maxn=1e5+5;
const int MOD=1e9+7;
LL dep(LL x,LL y,LL z)//给定点(x,y,z)看到稳态能走多少步
{
LL len1=y-x,len2=z-y;
if(len1==len2)return 0;
else if(len1<len2)
{
LL k=len2/len1;
if(len2%len1==0)return (k-1)+dep(x+(k-1)*len1,y+(k-1)*len1,z);
else return k+dep(x+k*len1,y+k*len1,z);
}
else
{
LL k=len1/len2;
if(len1%len2==0)return (k-1)+dep(x,y-(k-1)*len2,z-(k-1)*len2);
else return k+dep(x,y-k*len2,z-k*len2);
}
}
void Update(LL deep,LL &x,LL &y,LL &z)//给定步数,看能向上走到哪个点
{
LL len1=y-x,len2=z-y;
if(len1==len2 || deep==0)return ;
else if(len1<len2)
{
LL k=len2/len1;
if(len2%len1==0)
{
int t=min((k-1),deep);
Update(deep-t,x+=t*len1,y+=t*len1,z);
}
else
{
int t=min(k,deep);
Update(deep-t,x+=t*len1,y+=t*len1,z);
}
}
else if(len1>len2)
{
LL k=len1/len2;
if(len1%len2==0)
{
LL t=min((k-1),deep);
Update(deep-t,x,y-=t*len2,z-=t*len2);
}
else
{
LL t=min(k,deep);
Update(deep-t,x,y-=t*len2,z-=t*len2);
}
}
}
int main()
{
LL a[3],b[3];
while(cin>>a[0]>>a[1]>>a[2]>>b[0]>>b[1]>>b[2])
{
sort(a,a+3);
sort(b,b+3);
LL x1,y1,z1,x2,y2,z2;
x1=a[0],y1=a[1],z1=a[2],x2=b[0],y2=b[1],z2=b[2];
LL x3=x1,y3=y1,z3=z1,x4=x2,y4=y2,z4=z2;
LL dd1=dep(x1,y1,z1);
LL dd2=dep(x2,y2,z2);
Update(dd1,x3,y3,z3);
Update(dd2,x4,y4,z4);
if(x3!=x4 || y3!=y4 || z3!=z4)
{
puts("NO");
continue;
}
LL d1=0;//表示移动到相同深度需要走几步
if(dd1<=dd2)
{
Update(dd2-dd1,x2,y2,z2);
d1+=dd2-dd1;
}
else
{
Update(dd1-dd2,x1,y1,z1);
d1+=dd1-dd2;
}
dd1=min(dd1,dd2);
LL L=0,R=dd1,mid=dd1>>1;
LL d2;//表示lca到稳态的距离
while(L<=R)
{
mid=L+R>>1;
x3=x1,y3=y1,z3=z1;
x4=x2,y4=y2,z4=z2;
Update(dd1-mid,x3,y3,z3);//dd1-mid表示需要走的距离
Update(dd1-mid,x4,y4,z4);
if(x3==x4 && y3==y4 && z3==z4)
{
L=mid+1;
d2=mid;//成功了才记录答案
}
else R=mid-1;
}
puts("YES");
cout<<d1+dep(x1,y1,z1)+dep(x2,y2,z2)-d2*2<<endl;
}
}