联邦学习学习笔记——论文理解《Communication-Efficient Learning of Deep Networks from Decentralized Data》

Google — Federated Learning

原文：《Communication-Efficient Learning of Deep Networks from Decentralized Data》

最近研读了这篇提出了联邦学习（Federated Learning）的文章，内容主要是对原文的理解和整理，希望能帮助正在了解联邦学习的小伙伴们。

⚠️笔者也是刚开始了解FL，所以也可能有些地方理解不到位或有错误，者希望能和大家交流，共同进步~

• 一、研究背景

  移动通信设备中有许多有用的数据，训练模型后可以提高用户体验；但是，这些数据通常是敏感的或者很庞大的，不能直接上传到data center，使用传统的方法训练模型。

  Modern mobile devices have access to a wealth of data suitable for learning models, which in turn can greatly improve the user experience on the device. For example, language models can improve speech recognition and text entry, and image models can automatically select good photos.However, this rich data is often privacy sensitive, large in quantity, or both, which may preclude logging to the data center and training there using conventional approaches.

• 二、主要研究内容

提出了一种训练模型的替代方法Federated Learning

• leaves the training data distributed on the mobile devices；

  • learns a shared model by aggregating locally-computed updates；

  We advocate an alternative that leaves the training data distributed on the mobile devices, and learns a shared model by aggregating locally-computed updates. We term this decentralized approach Federated Learning.

• 提出一种实用的联邦学习算法——迭代的模型平均；

  • 适用于unbalanced and non-IID data distributions；
  • 通信成本是主要的约束条件，与同步随机梯度下降相比减少了10–100倍。

  We present a practical method for the federated learning of deep networks based on iterative model averaging, and conduct an extensive empirical evaluation, considering five different model architectures and four datasets. These experiments demonstrate the approach is robust to the unbalanced and non-IID data distributions that are a defining characteristic of this setting. Communication costs are the principal constraint, and we show a reduction in required communication rounds by 10–100× as compared to synchronized stochastic gradient descent.

• 提出了FederatedAveraging算法；robust to unbalanced and non-IID data distributions；reduce the rounds of communication needed to train

  More concretely, we introduce the FederatedAveraging algorithm, which combines local stochastic gradient descent (SGD) on each client with a server that performs model averaging. We perform extensive experiments on this algorithm, demonstrating it is robust to unbalanced and non-IID data distributions, and can reduce the rounds of communication needed to train a deep network on decentralized data by orders of magnitude.

• 三、联邦学习（Federated Learning）

  • FL的数据应具有以下特性（标准）：
  1. 训练来自移动设备的真实数据比数据中心提供的代理数据具有明显的优势；
  2. 数据是隐私敏感的或较大规模的，不需要仅出于训练模型的目的将其记录在数据中心；
  3. 对于监督任务，可以从用户交互中自然地推断出数据的标签。

  Federated Learning Ideal problems for federated learn- ing have the following properties: 1) Training on real-world data from mobile devices provides a distinct advantage over training on proxy data that is generally available in the data center. 2) This data is privacy sensitive or large in size (compared to the size of the model), so it is preferable not to log it to the data center purely for the purpose of model training (in service of the focused collection principle). 3) For supervised tasks, labels on the data can be inferred naturally from user interaction.

  • 许多 移动设备上的智能应用有满足上述标准的数据
  1. image classification: predicting which photos are most likely to be shared.
  2. language models: used to improve voice recognition and text entry on touch-screen keyboards.

  数据是敏感的： 用户的照片或键盘输入的文本；

  数据的分布也与代理数据提供的不同， 更有用户特点和优势；

  数据的标签也是可以直接获得的：比如用户的照片和输入的文字等本身就是带标签的；照片可以通过用户的交互操作进行打标签（删除、分享、查看）。

  同时，这两个任务都非常适合学习神经网络。 对于图像分类，前馈深层网络，特别是卷积网络（LeCun等，1998； Krizhevsky等，2012）；对于语言模型，神经网络，LSTM（Hochreiter和Schmidhuber，1997； Kim等，2015）。

  The potential training data for both these tasks (all the photos a user takes and everything they type ) can be privacy sensitive. The distributions from which these examples are drawn are also likely to differ substantially from easily available proxy datasets: the use of language in chat and text messages is generally much different than standard language corpora, e.g., Wikipedia and other web documents; the photos people take on their phone are likely quite different than typical Flickr photos. And finally, the labels for these problems are directly available: entered text is self-labeled for learning a language model, and photo labels can be defined by natural user interaction with their photo app (which photos are deleted, shared, or viewed).

• 四、隐私（Privacy）

1. FL 传输的信息是改进特定模型所必需的最小更新（隐私利益的强度取决于更新的内容）;

2. 更新本身是短暂的，所包含的信息绝不会超过原始训练数据且通常会少得多；

3. 聚合算法不需要更新源（不需要知道用户是谁？），因此，可以通过混合网络（例如Tor）或通过受信任的第三方传输更新而无需标识元数据。

4. 在本文的最后，简要地讨论了将联合学习与安全的多方计算和差分隐私相结合的可能性。

   Privacy Federated learning has distinct privacy advantages compared to data center training on persisted data. Holding even an “anonymized” dataset can still put user privacy at risk via joins with other data (Sweeney, 2000). In contrast, the information transmitted for federated learning is the minimal update necessary to improve a particular model (naturally, the strength of the privacy benefit depends on the content of the updates.) The updates themselves can (and should) be ephemeral. They will never contain more information than the raw training data (by the data processing inequality), and will generally contain much less. Further, the source of the updates is not needed by the aggregation algorithm, so updates can be transmitted without identifying meta-data over a mix network such as Tor (Chaum, 1981) or via a trusted third party. We briefly discuss the possibility of combining federated learning with secure multiparty computation and differential privacy at the end of the paper.

• 五、联邦优化（Federated Optimization）

  • 联邦优化： 隐含在联邦学习中的优化问题（与分布式优化问题对比）
  • 联邦优化问题的关键属性（与典型的分布式优化问题对比）
  1. 用户数据非独立同分布： 特定的用户数据不能代表用户的整体分布；
  2. 用户数据量不平衡： 数据量不均衡，因为有的用户使用多，有的用户使用少；
  3. 用户（分布）是大规模的： 参与优化的 用户数＞平均每个用户的数据量；
  4. 用户端设备通信限制： 移动设备经常掉线、速度缓慢、费用昂贵。

  Non-IID The training data on a given client is typically based on the usage of the mobile device by a particular user, and hence any particular user’s local dataset will not be representative of the population distribution.

  Unbalanced Similarly, some users will make much heavier use of the service or app than others, leading to varying amounts of local training data.

  Massively distributed We expect the number of clients participating in an optimization to be much larger than the average number of examples per client.

  Limited communication Mobile devices are frequently offline or on slow or expensive connections.

⚠️重点： 联邦优化问题中的non-IID[1]和unbalanced[2]特性，以及通信约束中的关键性质。

• 实际部署的联邦优化系统还须解决许多实际问题：

1. 随着数据添加和删除而不断改变的客户端数据集；
2. 客户端（更新）的可用性与其本地数据分布有着复杂的关系；
3. 从来不响应或发送信息的客户端会损坏更新。

In this work, our emphasis is on the non-IID and unbalanced properties of the optimization, as well as the critical nature of the communication constraints. A deployed federated optimization system must also address a myriad of practical issues: client datasets that change as data is added and deleted; client availability that correlates with the local data distribution in complex ways; and clients that never respond or send corrupted updates.

注：这些实际问题超出了当前工作的范围；本文使用了适合实验的可控环境，且仍解决了客户端可用性、不平衡和non-IID数据的关键问题。

These issues are beyond the scope of the current work; instead, we use a controlled environment that is suitable for experiments, but still address the key issues of client availability and unbalanced and non-IID data.

• 六、优化方法（基本思路&优化公式）

  • 执行思路：

    假设：同步更新方案在各轮通信中进行；有一组固定的客户端集合，大小为K，每个客户端都有一个固定的本地数据集；

  1. 在每轮更新开始时，随机选择部分客户端，大小为C-fraction（应该是比例，C≤1）；
  2. 然后，服务器将当前的全局算法的状态发送给这些客户（例如，当前的模型参数）；
  3. 然后，每个客户端都基于全局状态及其本地数据集执行本地计算，并将更新发送到服务器；
  4. 最后，服务器将这些更新应用于其全局状态，然后重复该过程。

  We assume a synchronous update scheme that proceeds in rounds of communication. There is a fixed set of K clients, each with a fixed local dataset. At the beginning of each round, a random fraction C of clients is selected, and the server sends the current global algorithm state to each of these clients (e.g., the current model parameters). Each client then performs local computation based on the global state and its local dataset, and sends an update to the server. The server then applies these updates to its global state, and the process repeats.

  • 非凸神经网络的目标函数

  While we focus on non-convex neural network objectives, the algorithm we consider is applicable to any finite-sum objective of the form:

  $$\underset{w\in {\mathbb{R}}^d}{\min }f(w),\text{ where }f(w)\stackrel{\text{ def }}{=}\frac{1}{n}\sum _{i=1}^n{f}_i(w)$$

  对于机器学习问题，我们通常定义fi(w) = L(xi,yi;w)；假设数据分布在K个客户端，Dk代表客户端k数据点的集合，nk为Dk的大小，目标函数可以重写为：

  $$f(w)=\sum _{k=1}^K\frac{n_k}{n}{F}_k(w)\text{ where }{F}_k(w)=\frac{1}{n_k}\sum _{i\in {\mathcal{P}}_k}{f}_i(w)$$

  如果划分Dk是所有用户数据的随机取样，则目标函数f(w)就等价于损失函数关于Dk的期望：

  $${\mathbb{E}}_{{\mathcal{P}}_k}\left[F_k(w)\right]=f(w)$$

  （这就是传统的分布式优化问题的独立同分布假设）

  • non-IID：指的是这个等式不成立的情况（即，Fk可以是f任意坏的近似）

  we refer to the case where this does not hold (that is, Fk could be an arbitrarily bad approximation to f) as the non-IID setting.

• 七、通信成本与计算成本的平衡

  • 在data center的优化问题中，通信成本相对较小，而计算成本占主导地位，重点是可以使用GPU来降低这些成本；
  • 在联合优化中，一方面，通信成本占主导地位：
  1. 我们通常会受到1 MB / s或更小的上传带宽的限制；
  2. 并且客户通常只会在充电，插入电源和不计量的Wi-Fi连接时自愿参与优化；
  3. 希望每个客户每天只参加少量的更新回合。
  • 另一方面，计算成本相对较小：
  1. 任何单个设备上的数据集都比总数据集的大小小；
  2. 现代智能手机具有相对较快的处理器（包括GPU）

  ⚠️因此，我们的目标是使用额外的计算，以减少训练模型所需的通信次数。

  • 两种方法来添加计算量：
  1. 提高并行性：在每个通信回合之间使用更多的客户端独立工作；
  2. 增加每个客户端的计算量： 不像梯度计算那样执行简单的计算，而是每个客户端在每个通信回合之间执行更复杂的计算。

  ⚠️我们研究了这两种方法，但是一旦使用了最低级别的客户端并行性，我们实现的加速主要是由于在每个客户端上添加了更多的计算。

Thus, our goal is to use additional computation in order to decrease the number of rounds of communication needed to train a model. There are two primary ways we can add computation: 1) increased parallelism, where we use more clients working independently between each communication round; and, 2) increased computation on each client, where rather than performing a simple computation like a gradient calculation, each client performs a more complex calculation between each communication round. We investigate both of these approaches, but the speedups we achieve are due primarily to adding more computation on each client, once a minimum level of parallelism over clients is used.

• 八、相关工作

  • McDonald等人已经研究了通过对本地训练模型进行迭代平均来进行分布式训练感知机（2010）；Povey等人研究了用于语音识别DNN（2015）；张等研究了一种具有 “软”平均的异步方法（2015）。

  存在的问题： 这些工作仅考虑集群/数据中心设置（最多16个工作人员，基于快速网络的挂钟时间），不考虑不平衡且非IID的数据集。 我们将这种风格的算法调整为适用于联邦学习的设置，并执行适当的经验评估，该评估提出的问题与data center中的问题不同，并且需要不同的方法。

  Distributed training by iteratively averaging locally trained models has been studied by McDonald et al. (2010) for the perceptron and Povey et al. (2015) for speech recognition DNNs. Zhang et al. (2015) studies an asynchronous approach with “soft” averaging. These works only consider the cluster / data center setting (at most 16 workers, wall-clock time based on fast networks), and do not consider datasets that are unbalanced and non-IID, properties that are essential to the federated learning setting. We adapt this style of algorithm to the federated setting and perform the appropriate empirical evaluation, which asks different questions than those relevant in the data center setting, and requires different methodology.

  • Shokri和Shmatikov的工作有多种联系（2015）：他们专注于训练深层网络，强调隐私的重要性，并通过在每一轮通信中仅共享一部分参数来解决通信成本。

  存在的问题： 没有考虑不平衡和非IID数据，因此经验评估是有限的。

  The work of Shokri and Shmatikov (2015) is related in several ways: they focus on training deep networks, emphasize the importance of privacy, and address communication costs by only sharing a subset of the parameters during each round of communication; however, they also do not consider unbalanced and non-IID data, and the empirical evaluation is limited. ref: Reza Shokri and Vitaly Shmatikov. Privacy-preserving deep learning. CCS, 2015.

  • 在凸设置（凸优化）中，分布式优化和估计问题受到了极大关注（Balcan等，2012； Fercoq等，2014； Shamir和Srebro，2014），并且某些算法确实专门针对通信效率（Shamir et al。，2013; Yang，2013; Ma et al。，2015; Zhang and Xiao，2015）。

  存在的问题： 假设凸优化；这些现有工作通常还要求客户端数量＜客户端的平均数据量；数据以IID方式分布在客户端之间；并且每个节点（客户端？）都具有相同的数据点数量（平衡性）。联邦优化的设置中违反了所有这些假设。

  In the convex setting, the problem of distributed optimization and estimation has received significant attention (Balcan et al., 2012; Fercoq et al., 2014; Shamir and Srebro, 2014), and some algorithms do focus specifically on communication efficiency (Shamir et al., 2013; Yang, 2013; Ma et al., 2015; Zhang and Xiao, 2015). In addition to assuming convexity, this existing work generally requires that the number of clients is much smaller than the number of examples per client, that the data is distributed across the clients in IID fashion, and that each node has an identical number of data points — all of these assumptions are violated in the federated optimization setting.

  • SGD的异步分布式形式也已用于训练神经网络，例如Dean等（2012），但这些方法在联邦学习中需要进行大量更新。
  • 众多（参数化）算法中，我们最终考虑的一个是简单一次平均simple one-shot averaging，其中每个客户解决的模型将其本地数据的损失降到最低（可能是正则化的），然后将这些模型取平均值以生成最终的全局模型。这种方法已经在带有IID数据的凸情况下进行了广泛的研究，众所周知，在最坏的情况下，生成的全局模型并不比在单个客户端上训练模型更好（Zhang等人，2012； Arjevani和Shamir，2015； Zinkevich等，2010）。

  Asynchronous distributed forms of SGD have also been applied to training neural net- works, e.g., Dean et al. (2012), but these approaches require a prohibitive number of updates in the federated setting. One endpoint of the (parameterized) algorithm family we consider is simple one-shot averaging, where each client solves for the model that minimizes (possibly regularized) loss on their local data, and these models are averaged to produce the final global model. This approach has been studied extensively in the convex case with IID data, and it is known that in the worst-case, the global model produced is no better than training a model on a single client (Zhang et al., 2012; Arjevani and Shamir, 2015; Zinkevich et al., 2010).

• 九、The FederatedAveraging(FedAvg) Algorithm

  • 随机梯度下降的重要性
  1. 深度学习的最新成功应用几乎都依赖于随机梯度下降（SGD） 的变体进行优化；
  2. 实际上，许多进展可以理解为通过调整模型的结构（或者损失函数），使其更易于使用简单的gradient-based methods进行优化（Goodfellow等，2016）。

  因此，从SGD开始构建用于联邦优化的算法。

  The recent multitude of successful applications of deep learning have almost exclusively relied on variants of stochastic gradient descent (SGD) for optimization; in fact, many advances can be understood as adapting the structure of the model (and hence the loss function) to be more amenable to optimization by simple gradient-based methods (Goodfellow et al., 2016). Thus, it is natural that we build algorithms for federated optimization by starting from SGD.

  • Baseline算法——FederatedSGD（FedSGD）

  直观方法：SGD可以直接应用于联邦优化，即每轮在随机选择的客户端上进行一次梯度计算。

  问题： 计算效率很高，但需要进行大量轮次训练才能生成好的模型。

  SGD can be applied naively to the federated optimization problem, where a single batch gradient calculation (say on a randomly selected client) is done per round of communication. This approach is computationally efficient, but requires very large numbers of rounds of training to produce good models (e.g., even using an advanced approach like batch normalization, Ioffe and Szegedy (2015) trained MNIST for 50000 steps on minibatches of size 60). We consider this baseline in our CIFAR-10 experiments.

  基线算法：大批量同步SGD（实验表明：在data center中是最先进的，优于异步方法）。

  FL形式： 每轮在clients中选择C-fraction，计算这些clients的所有数据的损失函数梯度。

  参数C： 控制global batch size；C = 1即全批（非随机）梯度下降。

  In the federated setting, there is little cost in wall-clock time to involving more clients, and so for our baseline we use large-batch synchronous SGD; experiments by Chen et al. (2016) show this approach is state-of-the-art in the data center setting, where it outperforms asynchronous approaches. To apply this approach in the federated setting, we select a C-fraction of clients on each round, and computes the gradient of the loss over all the data held by these clients. Thus, C controls the global batch size, with C = 1 corresponding to full-batch (non-stochastic) gradient descent. We refer to this baseline algorithm as FederatedSGD (or FedSGD).

  • FedSGD vs. FedAvg
    （这是我自己对FedSGD和FedAvg关系的理解）
    

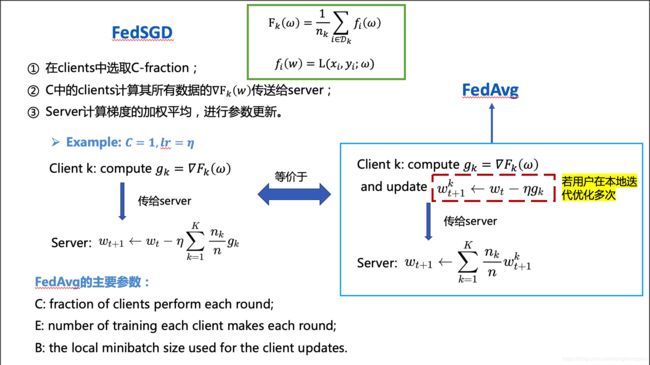
  主要区别：FedAvg相当于FedSGD在用户本地多次梯度更新；

  主要参数：C、B、E

  B=∞： 代表minibatch=用户本地全部数据

  B=∞ & E = 1： FedAvg 等价于 FedSGD

  The amount of computation is controlled by three key parameters: C, the fraction of clients that perform computation on each round; E, then number of training passes each client makes over its local dataset on each round; and B, the local minibatch size used for the client updates. We write B = ∞ to indicate that the full local dataset is treated as a single minibatch. Thus, at one endpoint of this algorithm family, we can take B = ∞ and E = 1 which corresponds exactly to FedSGD. Complete pseudo-code is given in Algorithm 1.

  • 模型平均的效果分析

  对于一般的非凸目标函数，参数空间中的平均模型可能会产生任意不好的模型结果。 按照Goodfellow等人（2015年）的方法 ，当我们平均两个从不同初始条件训练的MNIST数字识别模型时，我们恰好看到了这种不良结果（图1，左）。注：使用“2NN” multi-layer perceptron模型。
  
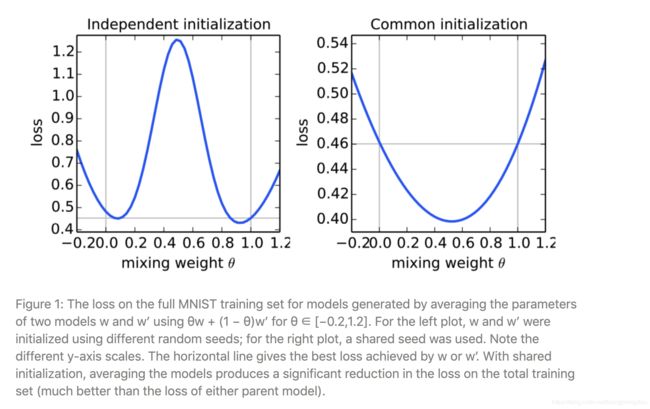
  最近的工作表明，在实践中，充分超参数的神经网络效果良好，更不容易出现不好的局部极小值（Dauphin等，2014; Goodfellow等，2015; Choromanska等，2015）。

  从相同的随机初始化开始两个模型，然后在不同的数据子集上对每个模型进行独立训练，朴素的参数平均效果很好（图1，右）。

  • 与Dropout training的关系

  Dropout training也为模型平均提供了一些直觉。

  Dropout training可以理解为”不同体系结构（clients）共享参数的平均模型“

  The success of dropout training also provides some intuition for the success of our model averaging scheme; dropout training can be interpreted as averaging models of different architectures which share parameters, and the inference- time scaling of the model parameters is analogous to the model averaging used in FedAvg (Srivastava et al., 2014).

• 十、实验结果

  • 任务： 图像分类、语言建模任务
  • 数据集：
  1. 首先选择一个大小适中的代理数据集，以便我们可以彻底研究FedAvg算法的超参数。 （虽然每次训练的规模都比较小，但我们为这些实验训练了2000多个个体模型。 ）
  2. 然后，我们介绍基准CIFAR-10图像分类任务的结果。
  3. 为了证明FedAvg在数据自然分区的实际问题上的有效性，评估了一项大型语言建模任务。

  • 模型设置（three model families on two datasets）

  • Two for MINIST digit recognition（图像分类）

    Model 1: A simple multilayer-perceptron

    A simple multilayer-perceptron with 2-hidden layers with 200 units each using ReLu activations (199,210 total parameters), which we refer to as the MNIST.

    Model 2: A CNN

    A CNN with two 5×5 convolution layers (the first with 32 channels, the second with 64, each followed with 2×2 max pooling), a fully connected layer with
    512 units and ReLu activation, and a final softmax output layer (1,663,370 total parameters).

    两种数据划分（IID & non-IID）

    IID：将数据打乱，100个clients，平均每个clients有600个examples；

    non-IID：按照数字标签（0-9）对数据进行排序，然后划分为200个大小为300的”片段“，然后给100个clients分配2个”片段“。（每人600条数据，且最多有两个数字标签的数据）

    We study two ways of partitioning the MNIST data over clients: IID, where the data is shuffled, and then partitioned into 100 clients each receiving 600 examples, and Non-IID, where we first sort the data by digit label, divide it into 200 shards of size 300, and assign each of 100 clients 2 shards. This is a pathological non-IID partition of the data, as most clients will only have examples of two digits. Thus, this lets us explore the degree to which our algorithms will break on highly non-IID data. Both of these partitions are balanced, however.

  • Language Modeling for Works of Shakespeare

    数据集： 威廉·莎士比亚全集

    数据划分： 用至少两行为每个剧中的每个角色构造一个客户数据集。

    共1146个clients（角色），每个client有80%的训练行数据，和20%的测试行数据；训练集中有3,564,579个字符，在测试集中具有870,014个字符。

    该数据基本是不平衡的，许多角色只有几行，而有些角色有很多行；测试集不是随机的样本，而是每个剧本按时间顺序将行分为训练集与测试集。

    此外，使用相同的训练/测试拆分，还构造了平衡的IID版本的数据集，也有1146个客户端。

    For language modeling, we built a dataset from The Complete Works of William Shakespeare. We construct a client dataset for each speaking role in each play with at least two lines. This produced a dataset with 1146 clients.

    模型设计： A stacked character-level LSTM language model

    任务： 读取一行中的每个字符后，会预测下一个字符（Kim等人，2015）。

    The model takes a series of characters as input and embeds each of these into a learned 8 dimensional space. The embedded characters are then processed through 2 LSTM layers, each with 256 nodes. Finally the output of the second LSTM layer is sent to a softmax output layer with one node per character. The full model has 866,578 parameters, and we trained using an unroll length of 80 characters.

  • 特殊说明：SGD对学习速率参数η的调整很敏感。

  SGD is sensitive to the tuning of the learning-rate parameter η. The results reported here are based on training over a sufficiently wide grid of learning rates (typically 11-13 values for η on a multiplicative grid of resolution 10^-3 or 10^-6 ). We checked to ensure the best learning rates were in the middle of our grids, and that there was not a significant difference between the best learning rates. Unless otherwise noted, we plot metrics for the best performing rate selected individually for each x-axis value. We find that the optimal learning rates do not vary too much as a function of the other parameters.

• 实验结果

  • proxy dataset 分析超参数参数C、E、B对实验结果的影响，以便后续研究

    • Increasing parallelism 提高并行性（fix E，analyze C & B）

      • 对client fraction C进行实验（**C：**控制多客户端并行的数量，即每轮选取多少客户端）

      改变参数C，测试集准确性达到目标时的通信轮数，以及与Baseline C=0的对比。

      Table 1: Effect of the client fraction C on the MNIST 2NN with E = 1 and CNN with E = 5. Note C = 0. 0 corresponds to one client per round. Each table entry gives the number of rounds of communication necessary to achieve a test-set accuracy of 97% for the 2NN and 99% for the CNN, along with the speedup relative to the C = 0 baseline. Five runs with the large batch size did not reach the target accuracy in the allowed time.

      • 结果分析——B&C的影响

      With ①B = ∞ (for MNIST processing all 600 client examples as a single batch per round), there is only a small advantage in increasing the client fraction. Using the smaller batch size ②B = 10 shows a significant improvement in using C ≥ 0.1, especially in the non-IID case. Based on these results, for most of the remainder of our experiments we fix C = 0.1, which strikes a good balance between computational efficiency and convergence rate. Comparing the number of rounds for the B=∞ and B=10 columns in Table 1 shows a dramatic speedup, which we investigate next.

      注：B=∞ and B=10 之间下降明显，之后会研究

    • Increasing computation per client 提高客户端计算量（fix C=0.1，analyze E & B）

      • 实验设置&结果

      
      Figure 2: Test set accuracy vs. communication rounds for the MNIST CNN (IID and then pathological non-IID) and Shakespeare LSTM (IID and then by Play&Role) with C = 0.1 and optimized η. The gray lines show the target accuracies used in Table 2. Plots for the 2NN are given as Figure 7 in Appendix A.
      
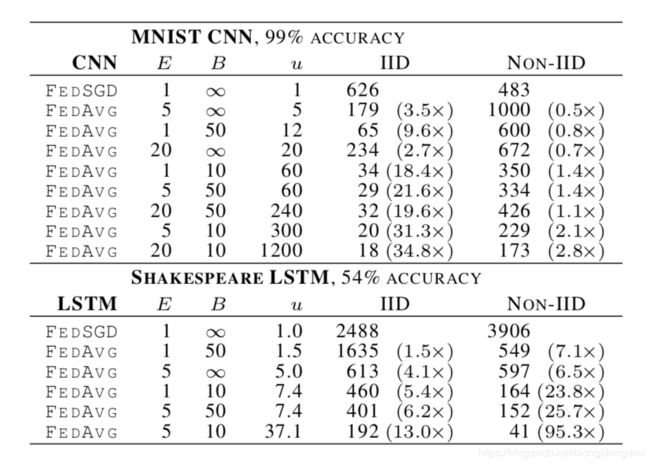
      Table 2: Number of communication rounds to reach a target accuracy for FedAvg, versus FedSGD (first row, E = 1 and B = ∞). The u column gives u = En/(KB), the expected number of updates per round.

      图2：每轮添加更多本地SGD更新可以大大降低通信成本，表2量化了这些加速。

      $$u=\left(\mathbb{E}\left[n_k\right]/B\right)E=nE/(KB)$$

      u: 每个客户端每回合的预期更新次数，期望值（E[]）大于随机抽取k（n/K）。

      We order the rows in each section of Table 2 by this statistic. We see that increasing u by varying both E and B is effective. As long as B is large enough to take full advantage of available parallelism on the client hardware, there is essentially no cost in computation time for lowering it, and so in practice this should be the first parameter tuned.

      
      Table 4: Speedups in the number of communication rounds to reach a target accuracy of 97% for FedAvg, versus FedSGD (first row) on the MNIST 2NN model.

      • MINIST数据集——CNN和2NN

      对于IID和non-IID的数据，提高E和B都能减少通信轮数，并且对于不同pair的手写数据集，模型平均竟然有一些效果，说明了方法具有鲁棒性。

      For the IID partition of the MNIST data, using more computation per client decreases the number of rounds to reach the target accuracy by 35× for the CNN and 46× for the 2NN (see Table 4 for the 2NN). The speedups for the pathologically partitioned non-IID data are smaller, but still substantial (2.8 – 3.7×). It is impressive that averaging provides any advantage (vs. actually diverging) when we naively average the parameters of models trained on entirely different pairs of digits. Thus, we view this as strong evidence for the robustness of this approach.

      • 莎士比亚数据集——LSTM

      莎士比亚的不平衡和非IID分布数据（按角色扮演）更能代表我们期望用于实际应用中的数据分布。在非IID和不平衡数据上的训练更加容易（加速95倍，而平衡IID数据则为13倍）。 我们推测这主要是由于某些角色具有相对较大的本地数据集，这使得增加本地训练特别有价值。

      The unbalanced and non-IID distribution of the Shakespeare (by role in the play) is much more representative of the kind of data distribution we expect for real-world applications. Encouragingly, for this problem learning on the non-IID and unbalanced data is actually much easier (a 95× speedup vs 13× for the balanced IID data); we conjecture this is largely due to the fact some roles have relatively large local datasets, which makes increased local training particularly valuable.

      • 三个模型总结分析

      FedAvg收敛到比基准FedSGD模型更高的测试集准确性水平。（即使超出了绘制范围，这种趋势仍将继续。）例如，对于CNN，B =∞，E = 1 FedSGD模型最终在1200轮后达到了99.22％的准确度（并且在6000轮之后并没有进一步改善）；而B = 10，E = 20的FedAvg模型达到了300轮后达到99.44％。因此推测，除了降低通信成本外，模型平均还产生了与dropout正则化相似的优化效果。

      FedAvg具有一定的泛化能力，甚至可以优化训练损失（超出测试集精度的稳定水平）

      For all three model classes, FedAvg converges to a higher level of test-set accuracy than the baseline FedSGD models. This trend continues even if the lines are extended beyond the plotted ranges. For example, for the CNN the B = ∞, E = 1 FedSGD model eventually reaches 99.22% accuracy after 1200 rounds (and had not improved further after 6000 rounds), while the B = 10, E = 20 FedAvg model reaches an accuracy of 99.44% after 300 rounds. We conjecture that in addition to lowering communication costs, model averaging produces a regularization benefit similar to that achieved by dropout (Srivastava et al., 2014).

      We are primarily concerned with generalization performance, but FedAvg is effective at optimizing the training loss as well, even beyond the point where test-set accuracy plateaus. We observed similar behavior for all three model classes, and present plots for the MNIST CNN in Figure 6 in Appendix A.

    • Can we over-optimize on the client datasets? 能不能客户端”一直“优化下去？

      当前模型参数仅通过初始化影响每个Client Update中执行的优化。 当E→∞时，至少对于凸问题，并且无论初始化如何，都将达到全局最小值；对于非凸问题，只要初始化是在同一个”盆地“中，算法也会收敛到相同的局部最小值。

      可以这样说，我们希望，虽然一轮平均可以产生一个合理的模型，但是额外的几轮交流（和平均）不会产生进一步的改善。（不太理解）

      That is, we would expect that while one round of averaging might produce a reasonable model, additional rounds of communication (and averaging) would not produce further improvements.

      Figure 3 shows the impact of large E during initial training on the Shakespeare LSTM problem. Indeed, for very large numbers of local epochs, FedAvg can plateau or diverge. This result suggests that for some models, especially in the later stages of convergence, it may be useful to decay the amount of local computation per round (moving to smaller E or larger B) in the same way decaying learning rates can be useful. Figure 8 in Appendix A gives the analogous experiment for the MNIST CNN. Interestingly, for this model we see no significant degradation in the convergence rate for large values of E.

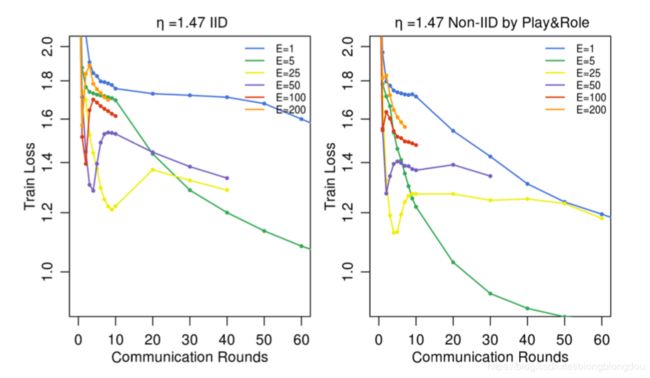      Figure 3: The effect of training for many local epochs (large E) between averaging steps, fixing B = 10 and C = 0.1 for the Shakespeare LSTM with a fixed learning rate η = 1.47.

      
      Figure 8: The effect of training for many local epochs (large E) between averaging steps, fixing B = 10 and C = 0.1. Training loss for the MNIST CNN. Note different learning rates and y-axis scales are used due to the difficulty of our pathological non-IID MNIST dataset.

  • CIFAR-10 dataset 进一步验证FedAvg的效果

    • 数据集： 由具有三个RGB通道的10类32x32图像组成；50,000个训练样本和10,000个测试样本。将数据划分为100个clients，每个client包含500个训练样本和100个测试样本。

    注：此数据没有自然的用户数据划分，因此考虑了均衡和IID设置。

    • 模型： 模型架构取自TensorFlow教程，包括2个卷积层、2个全连接层和1个线性转换层生成logit（共约106个参数）。

    注： 对于CIFAR数据集，最先进的方法已达到96.5％的测试准确度； 但是，使用标准的模型架构即可，因为目标是评估优化方法，而不是在此任务上获得最佳的准确性。

    We also ran experiments on the CIFAR-10 dataset (Krizhevsky, 2009) to further validate FedAvg. The dataset consists of 10 classes of 32x32 images with three RGB channels. There are 50,000 training examples and 10,000 testing examples, which we partitioned into 100 clients each containing 500 training and 100 testing examples; since there isn’t a natural user partitioning of this data, we considered the balanced and IID setting. The model architecture was taken from the TensorFlow tutorial (TensorFlow team, 2016), which consists of two convolutional layers followed by two fully connected layers and then a linear transformation layer to produce logits, for a total of about 106 parameters. Note that state-of-the-art approaches have achieved a test accuracy of 96.5% (Graham, 2014) for CIFAR; nevertheless, the standard model we use is sufficient for our needs, as our goal is to evaluate our optimization method, not achieve the best possible accuracy on this task.

    • 优化方法设置与结果

    Baseline：标准SGD，on 全部训练数据（无用户划分），minibatch=100；

    测试数据准确性：86%；训练次数：197,500 minibatch updates；

    FedAvg：可达到达到85％测试准确度，2000轮；

    注：对于所有算法，除了初始learning-rate外，还调整了learning-rate decay。

    表3给出了Baseline SGD，FedSGD和FedAvg达到三项不同精度目标所需轮数；

    图4给出了FedAvg与FedSGD的学习率曲线

    
    Table 3: Number of rounds and speedup relative to baseline SGD to reach a target test-set accuracy on CIFAR10. SGD used a minibatch size of 100. FedSGD and FedAvg used C = 0.1, with FedAvg using E = 5 and B = 50.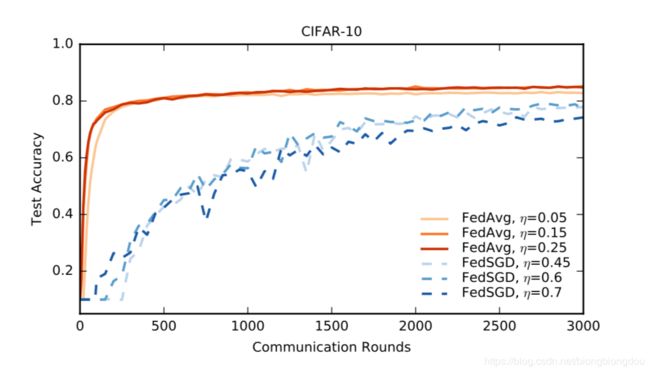

    
    Figure 4: Test accuracy versus communication for the CIFAR10 experiments. FedSGD uses a learning-rate decay of 0.9934 per round; FedAvg uses B = 50, learning-rate decay of 0.99 per round, and E = 5.

    其他发现： 对SGD和FedAvg进行minibatch B = 50的实验，可以将精度视为进行minibatch gradient calculations次数的函数。 我们希望SGD能表现得更好，因为在每次minibatch computation之后都会采取一个顺序步骤。 但是，如图9，对于适当的C和E值，FedAvg在每次minibatch computation中取得相似的进度。 此外，当SGD和FedAvg每轮只有一个client时（绿），准确性显着波动，而对更多clients进行平均则可以解决这一问题（黄）。

    
    Figure 9: Test accuracy versus number of minibatch gradient computations (B = 50). The baseline is standard sequential SGD, as compared to FedAvg with different client fractions C (recall C = 0 means one client per round), and different numbers of local epochs E.

  • Large-scale LSTM experiments

    • 数据集：训练数据来自大型社交网络的1000万个帖子。 将帖子按作者分组，共有超过500,000个客户。 此数据集是现实中用户移动设备上文本输入的代理数据。 将每个客户数据集限制为最多5000个字，并在来自不同作者的1e5个帖子的测试集上测试准确性。
    • 模型： 256 node LSTM on a vocabulary of 10,000 words；每个单词的输入和输出embedding维度为192，并与模型一起训练；共4,950,544个参数；使用10个词的展开。
    • 优化方法设置与结果

    注： 实验需要大量的计算资源，因此没有彻底探讨超参数。

    设置： 所有运行都每轮训练200个clients ; FedAvg使用B = 8，E =5。

    探索FedAvg和FedSGD在各种learning rate下的效果

    图5：显示了最佳学习率的单调学习曲线。 η= 0.4的FedSGD需要310轮才能达到8.1％的准确度，而η= 18.0的FedAvg仅在20轮就达到了8.5％的准确性（比FedSGD少15倍）。

    图10：不同lr，FedAvg的测试准确性差异要小得多。

    
    Figure 5: Monotonic learning curves for the large-scale language model word LSTM. Note that FedAvg allows the use of much larger learning rates than FedSGD.

    
    Figure 10: Learning curves for the large-scale language model word LSTM. Note that FedAvg allows the use of much larger learning rates than FedSGD, and also demonstrates much lower variance in accuracy across evaluation rounds.

• 总结与展望

  • 各种模型架构（多层感知器，两种不同的卷积神经网络， 两层字符LSTM和大规模词级LSTM）的实验结果表明：当FedAvg使用相对较少的交流轮次来训练高质量的模型时，联邦学习是实际可行的。

  Our experiments show that federated learning can be made practical, as FedAvg trains high-quality models using relatively few rounds of communication, as demonstrated by results on a variety of model architectures: a multi-layer perceptron, two different convolutional NNs, a two-layer character LSTM, and a large-scale word-level LSTM.

  • 尽管联合学习提供了许多实用的隐私优势，但通过差分隐私、多方安全计算或者它们的组合提供更强的隐私保证是未来工作的有趣方向。
    ⚠️这两类隐私保护技术自然地适用于FedAvg之类的同步算法。

  While federated learning offers many practical privacy benefits, providing stronger guarantees via differential privacy (Dwork and Roth, 2014; Duchi et al., 2014; Abadi et al., 2016), secure multi-party computation (Goryczka et al., 2013), or their combination is an interesting direction for future work. Note that both classes of techniques apply most naturally to synchronous algorithms like FedAvg.