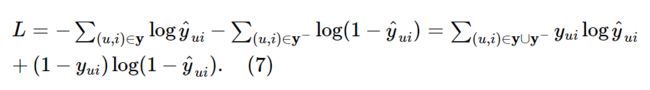复试 | 读书报告

1. Neural Collaborative Filtering

在这篇论文中，作者探索了用于协同过滤的神经网络结构，设计了一个通用框架NCF，并提出了三种实例：GMF，MLP和NeuMF，以不同的方式模拟用户-项目交互。

研究点

• 关于推荐系统的深度学习研究不多；
• 对user和item的交互行为（interaction）的建模大多使用MF，对user和item的隐特征使用内积计算，而这是一种线性方式。而通过引入user/item偏置提高MF效果也说明内积不足以捕捉到用户交互数据中的复杂结构信息。
• 在本文中，作者使用的是隐反馈，即只考虑user对item是否有interaction（比如点击、观看、购买），显式反馈通常包括评分、评论。此前的工作大多用DNN对图像、文本这类辅助信息建模,并未对本身这种interaction的行为进行建模，而深度学习号称能够逼近任意连续函数，就可以使用神经网络代替内积对user、item的interaction建模，去学习所谓的interaction function，提出一个通用框架NCF（Neural Collaborative Filtering）：

通用框架

• Input layer
  为了允许神经网络对协同过滤进行一个完整的处理，作者采用下图展示的多层感知机去模拟一个用户项目交互 $y_{ui}$ ，它的一层的输出作为下一层的输入。底部输入层包括两个特征向量 $v_u^U$ 和 $v_i^I$ ，分别用来描述用户 $u$ 和项目 $i$ ，并使用one-hot编码将它们转化为二值化稀疏向量。

• Embedding Layer
  它是一个全连接层，用来将输入层的稀疏表示映射为一个稠密向量（dense vector）。

• Neural CF Layers
  多个隐藏层实现非线性转化，文中使用的3层，ReLU激活函数

• Output Layer
  最后输出一个分数，最小化预测值和真实值的pointwise loss求解模型（也有一些模型最后使用pairwise loss求解的）

• Interaction function:
  
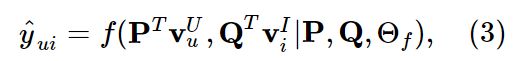
  其中 P∈RM×K， Q∈RN×K，分别表示用户和项目的潜在因素矩阵；Θj 表示交互函数 f 的模型参数。最后预测出来的值介于0和1之间。由于函数 f 被定义为多层神经网络，它可以被定制为：
  
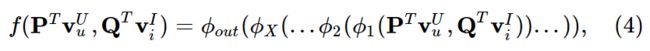
  其中 ϕout 和 ϕx 分别表示为输出层和第 x 个神经协作过滤（CF）层映射函数，总共有 X 个神经协作过滤（CF）层。

• 目标函数
  NCF方法需要去最小化的目标函数如下所示，并且可以通过使用随机梯度下降（SGD）来进行训练优化。
  

GMF（广义矩阵分解）模型

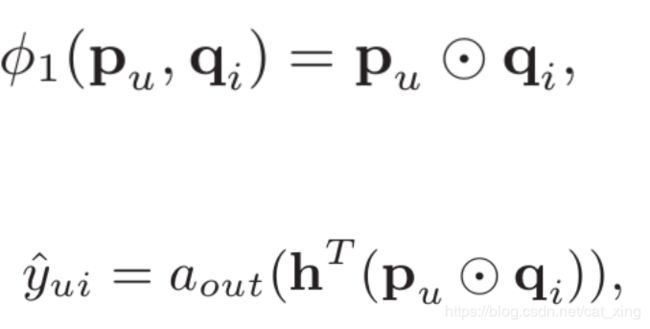
对于上面的通用模型，如果将embedding层的结果视为user和item的隐向量，h是权重，aout是激活函数，考虑h全是1，aout是个恒等函数，那么就变成了最一般的MF了，即MF是NCF的一个特例。如果将激活函数换成非线性函数，那么MF就拓展为非线性的了，比如考虑使用sigmoid函数。这个模型就称为GMF（Generalized Matrix Factorization）模型。

MLP（多层感知机）

作者还考虑使用标准MLP对user和item的interaction建模：

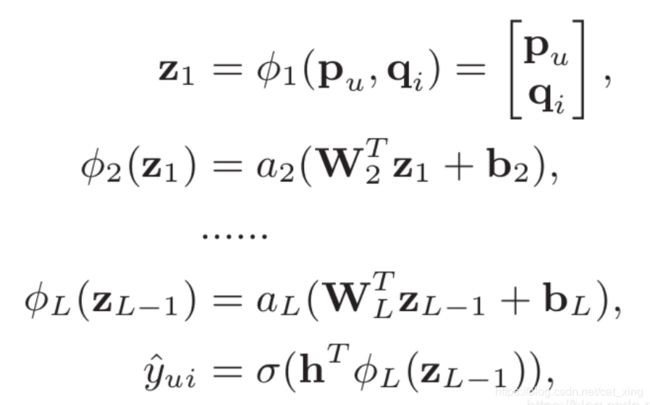
这里同样先通过映射获得user和item vector，但要注意,之前的MF vector和MLP vector虽然同为映射的向量，但绝对不一样，因为模型对隐向量的维度等要求是不一样的。然后将user和item vector输入到MLP中进行训练，重点是如何处理user和item vector，作者是直接将两个向量串联起来。

NeuMF

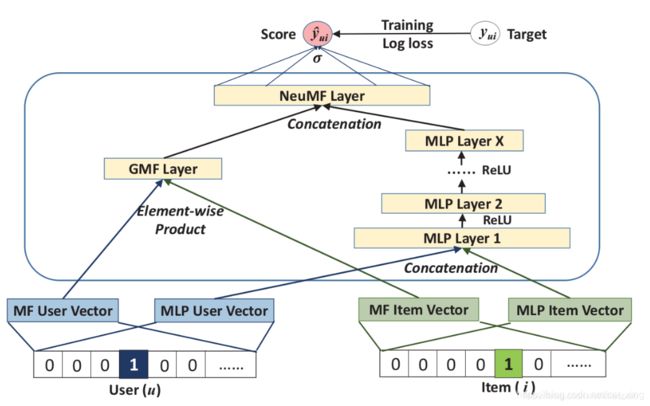
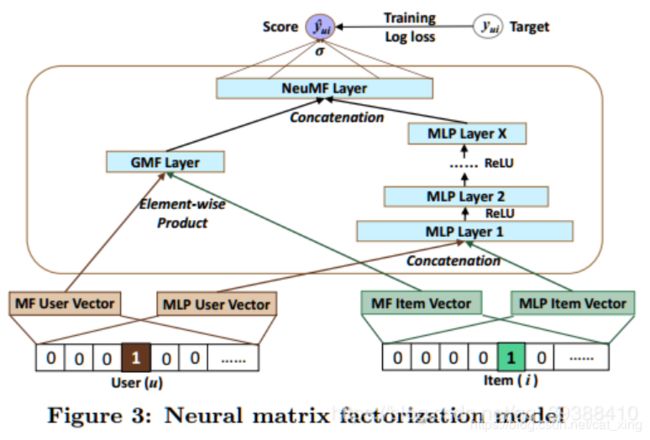
基于此，作者又提出了一个融合模型NeuMF（Neural matrix factorization model）。

由于不能强行要求GMF和MLP在输入时的隐向量维度一致，毕竟是两个不同的模型，所以分别做embedding。现在对两个模型的“输出”也不能做这种要求，因此作者想了个更好的办法：将两个模型的倒数第二层特征串联为一个特征，然后加层感知机：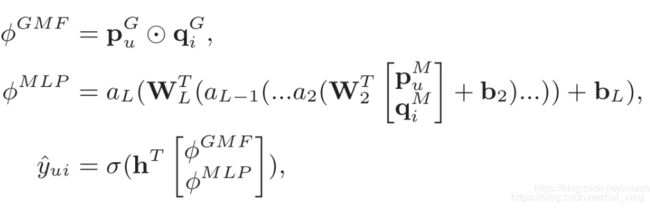

实验

• 数据集：MovieLens:经典电影评分数据集；pinterest数据集：一个图片类书签网站数据集。
• 评价指标：Hit Ratio和NDCG
• 对比方法: 1.ItemPop；2.item KNN；3.BPR；4.EALS
• 实验内容：
  1.NeuMF的性能；
  2.因为隐反馈是考虑0/1行为，那么其实就变成了二分类问题，观察采用log loss with negative sampling的方法后NeuMF的性能；
  3.考察隐藏层的深度对实验结果的影响
• 结论：融合了MF线性关系和MLP非线性关系的NeuMF模型效果最好；优化对数损失函数的合理性和有效性；隐层多对实验结果有提升。

---

个人感悟

• 基于神经网络的学习方法（NCF）为何向南博士在2017年提出，对比传统的CF网络，在得到user vector和item vector后，连接了MLP网络后，最终拟合输出，得到一个end-2-end的model。这套框架好处就是足够灵活，user和item侧的双塔设计可以加入任意side info的特征，而MLP网络也可以灵活的设计
• 基于NCF框架的方法基础原理是基于协同过滤，而协同过滤本质上又是在做user和item的矩阵分解，所以，基于NCF框架的方法本质上也是基于MF的方法。矩阵分解本质是尽可能将user和item的vector，通过各种方法去让user和item在映射后的空间中的向量尽可能接近（用向量点击或者向量的cosine距离直接衡量是否接近）。
• NCF框架对比CF方法最主要引入了MLP去拟合user和item的非线性关系，而不是直接通过inner product或者cosine去计算两者关系，提升了网络的拟合能力。然而MLP对于直接学习和捕获从mf提取的user和item vector能力其实并不强。在wsdm2018的一篇文章质疑的就是MLP对特征组合的拟合能力，该paper做了一组实验，使用1层的MLP网络去拟合数据；实验证明对于二维一阶的数据，也需要100个节点才能拟合；如果超过2阶，整个MLP的表现将会非常差。文章因此说明了DNN对于高阶信息的捕捉能力并不强，只能捕捉低阶信息。

---

改进方案

• 输入除了user和item的信息，还可以引入user和item各自的neighbor信息。
• 仅靠MLP想完全捕捉到特征的有效交叉其实是非常困难的。因此，可以考虑在embedding这里捕捉特征交叉，其实就是在MLP网络之前，利用更多的数学先验范式做特征交叉去提取特征。
• 可以在embedding layer之后，引入interaction map也就是特征交叉层，对于用户u的向量pu和物品i的向量qi，引入两者的outer-product。

---

---

---

2.Adversarial Attacks on Neural Networks for Graph Data

概述

这篇文章是KDD’18的best research paper，算是图对抗攻击的开山之作。这篇文章研究的是属性图上针对某个节点的节点分类攻击，也就是说对于一张属性图上的某个节点，通过施加一些图结构（加边、减边）或节点属性（加属性、减属性）上的扰动，使得模型对该节点分类预测错误。实验结果表明节点分类的准确率即使在采用很少的一点扰动的情况下也会明显下降。此外，本文采取的攻击是可迁移的，学习出来的攻击可以在只提供一点图信息的情况下成功的对其他的节点分类模型进行成功的攻击。

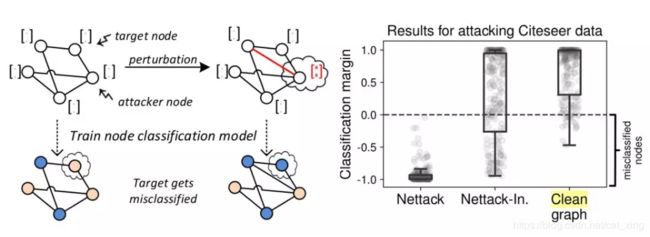
这篇文章将研究的图种类限定到了 Attributed Graph（属性图），即图既有节点特征，也有节点之间的结构特征。该文章默认攻击方知道图中全部的信息。攻击方的目标是通过制造一些“很难被注意到的”变化（节点属性或者图结构的变化）使得图分类器的错误率上升。

具体来说，对于我们要攻击的目标节点，我们要产生一个“干扰图”，使得产生的干扰图与原图区别不大，并且最大化新图上目标节点的分类概率和老图上目标节点分类概率的差距。

我们通过改变节点属性和图结构来产生干扰，作者具体定义了什么是节点层面和结构层面的干扰以及如何在保持节点属性和图结构的前提下产生干扰。

作者提出了一种名为 Nettack 的攻击模型用来产生干扰图，该模型定义了候选攻击方法以及计算攻击效果分数的函数，然后在节点属性和图结构两个维度上选择最优的加入干扰的方式。

该方法首先通过在一个代理模型（surrogate model）上进行模拟的攻击行为，然后将代理模型上面训练到结果迁移到实际的深度分类模型中，发现在深度分类器上面也可以达到很好的攻击效果。

该方法研究的深度图分类器有三种，分别为半监督的图卷积网络（GCN），列网络（Column Network）和无监督的深度游走（DeepWalk）模型。实验比较了一种随机方法和梯度攻击节点的方法，最终的实验结果表明 Nettack 模型有较好的攻击效果。

但是，这篇文章并没有讨论相应的防御方法，这可以作为未来的研究方向。

---

定义扰动代价

回顾图像对抗攻击，一个最直观的扰动代价定义方式就是扰动的数目，那么在图对抗攻击中显然也要有这样的约束，用$△$ 限制扰动的数目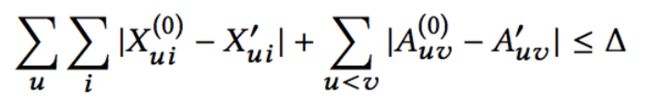：接下来考虑对图结构的扰动。对于一张图而言，最重要的结构相关的特征就是图的degree distribution，因此这里定义如果扰动后的图的degree distribution与原图很不一样，认为这样的扰动很容易被分辨。现实中的图往往服从幂律分布 ，对于一张图而言，它的幂律分布参数可以用下式近似：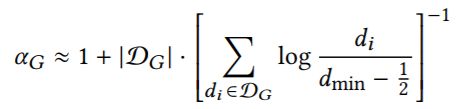
那么考虑如果原图和扰动后的图都属于同一个分布的采样，就认为两张图在结构上不可分辨，文章使用log-likelihood衡量某张图是否是一个概率分布的采样，用log-likelihood差衡量扰动的幅度:
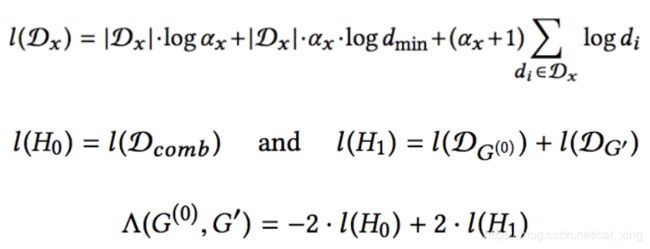如果 ，则认为结构扰动不可分辨。

除了图结构以外，也可以改动节点的属性，因此需要定义节点属性的扰动代价。作者认为对于节点属性而言，其最重要的判别依据应该是特征的共现关系。比如两个在原图中从未共现过的特征在扰动后的图中共现了，那么这样的扰动是容易被分辨的。首先建立图C = (F,E)， F 是特征的集合，E⊆F×F代表特征之间是否共现，令 表示节点u原有的特征。假如现在要对节点u 新增特征i ，需要满足下式条件才能认为不可分辨（删除某个特征不需要判断）：

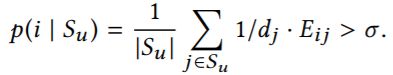
这个式子的含义相当于计算特征间共现概率的加权平均。而$d_j$ 用来度量特征的特殊性，对于一个与大量其他特征共现的特征，要削弱它的加权贡献。

生成攻击

攻击模型的loss如下式（最大化将某个节点预测为与原来结果不同类别的概率与原来结果概率的差）：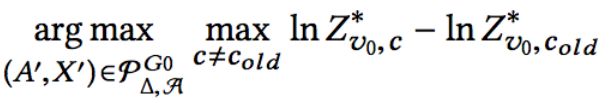
本文在一个代理模型上进行攻击，选择两层GCN并用恒等函数替换原来的激活函数，于是代理模型等于下式：

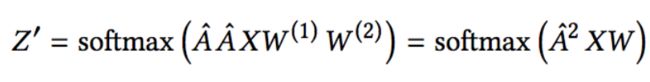
攻击目标是最大化目标节点$v_0$的log-probabilities的变化，因而softmax也可以拿掉（不影响大小关系），那么给定一个训练好的模型，权重参数为 W ，代理模型上的攻击损失可以定义为：

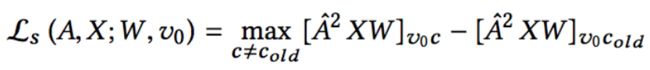
为了便于优化，定义两个函数分别评估结构扰动（增加／删除一条边）和属性扰动（增加／删除一个属性）对loss的影响。

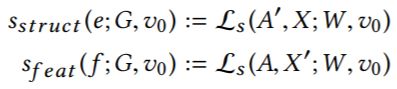
整个算法如下：
每一次扰动前根据当前状态建立一个可行（满足前面提到的不可分辨要求）的扰动解空间，选择能最大化扰动评估函数的那种扰动并施加，直到达到扰动数量$△$为止。

高效计算

要使得这个算法能够实际应用，有两个条件是要满足的，一个是s_struct和s_feat的计算要高效，另一个是能够高效的检查哪一个edge和feature的添加或删除是满足unnoticeable的。

score function的快速计算依赖于一个定理，当添加或者删除一个edge(m,n)的时候，有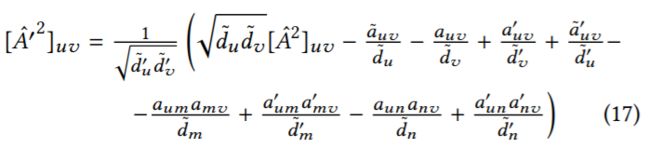而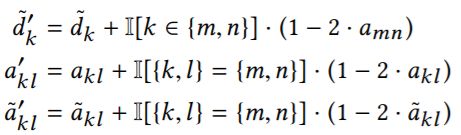这个公式使得能够在一个常量级时间段内得以计算，并且是以一种incremental的方式，只需要对改变量进行计算。

而对于feature attack来说，情况就简单得多，因为事先通过规则固定了要将target错分成哪一类，因此，选择最合适的node和feature只要对每一个node的feature进行求导即可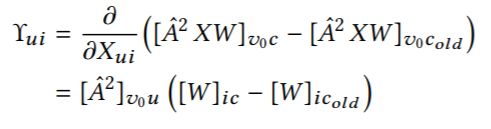之后选择一个指向允许方向的，绝对值最大的，这个指向允许方向的意思是，每个feature的取值只有0，1，因此如果feature是0，那么梯度指向正值，那就是可以的方向，可以将这个feature的值改成1了，如果梯度指向负值，那不行，feature不能取负的。并且在algorithm1中可以看到，structure和feature的attack并不是两者同时进行，而是看哪个带来的score的上升比较大，就取哪一种攻击方式，攻击一次整个graph就变了，因此再实施第二种攻击其实是不合理的，因为情况变了要重新计算。还有一个注意的是，在简化问题使得问题变得tractable的时候，W是没有变化的，也就是说并不像之前所说的是一个bi-level问题，而是固定了模型。

最后介绍的是candidate set的快速计算，也就是attack的时候，结构的改变和feature的改变受到限制而得到的一些可以进行的改变而得到的集合，前面提到过的。由于budget △限制和feature的unnoticeable change限制都很好用incremental的方式来进行检测，需要处理的就是structure attack的constraint的快速检测，这就又依赖于一个定理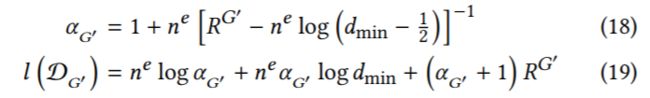其中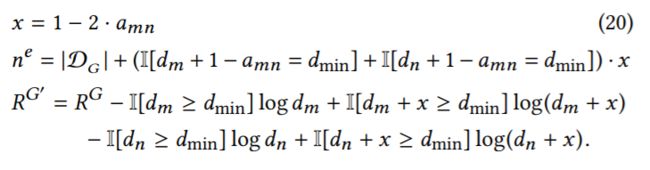有了这条定理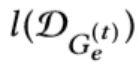，也可以以一种incremental的方式计算，新graph的degree distribution的改变是否超出要求，也就好判断了。

---

个人感悟

• 这篇论文被称为是图对抗攻击的开山之作，说明对抗攻击发展还十分稚嫩，还在不断寻找新的应用场景。由于图结构数据可以建模现实生活中的很多问题，现在也有很多研究者在研究这种问题，比如知识图谱等领域。拿知识图谱来举例，现在百度、阿里巴巴等公司都在搭建知识图谱，如果我能攻击知识图谱，在图上生成一些欺骗性的结点，比如虚假交易等行为，这会对整个公司带来很大损失，所以对图结构的攻击和防御都很有研究价值。
• 我认为现阶段对图结构的对抗攻击的局限在于以下两点：1.没有有效的防御算法。2.现阶段图深度学习发展还不完善，没有形成一个像图片卷积神经网络那样的完整体系。
• 论文的思想是对于要攻击的目标节点，产生一个干扰图，使得新图上的目标节点的分类概率和老图上目标节点的分类概率的差距最大，作者还提出了Nettack的攻击模型，总体的思路还是比较清晰的，不过，对于如何定义扰动代价以及生成攻击，我的理解还是不够深入，初看论文里的公式也感到比较吃力，也许是由于之前没有对抗攻击方面的经验吧。

---

改进方案

1. 这篇论文没有提及对图结构的防御问题，因此可以在防御问题上做进一步的研究。
2. 可以定义多钟约束条件，以免产生的对抗样本被另外一个新的指标检测到。
3. 可以使用元学习（meta learning）的方法，对节点分类任务的训练过程进行攻击，以实现在极小的扰动下大大降低图卷积网络（GCN）的表现。
4. 目前针对传统图模型算法例如随机游走（Random Walk），信度传播（Belief Propagation）的对抗攻击还很少，这也是一个未来的研究方向。

---

---

---

3.On Availability for Blockchain-Based Systems

概述

作者们在该论文中从现在两个主流的区块链，以太坊和比特币中，发现了区块链可用性的限制，证明了从区块链中读取数据的可用性很高，但是往区块链中写入数据（交易数据管理）的可用性就很低。

从以太坊的实验中发现，大量的交易中，有很多交易信息是没有被提交的，区块链中也没有明确的终止交易和重新提交的内在机制，这些交易就一直处于一种等待状态。最后，基于以上这些限制，作者们提出了一些技术来优化这些问题。

作者在这篇论文中调查了交易记录没有被提交的原因以及耗费长时间的原因：

• 网络重新排序也会造成很大的延迟。
• 调查研究用户定义的gas price、gas limit和block gas limit变量名所带来的影响。
• 制定将阻塞在交易池的交易终止的机制的必要性。

---

比特币交易的提交

在本节中，作者讨论了影响比特币提交时间的因素，并进行了实验验证。

影响交易提交时间的因素

• 交易手续费(transaction fee)
• 交易是否按顺序到达：如果一个交易比其所引用的父交易先到达，则被称为orphan。只有父交易提交后，子交易才能提交，否则子交易就会一直在mempool中等待。
• 锁定时间(locktimes)：这是一个用户可设置的参数，可使得某个交易在特定顺序的区块产生之前一直处于不可用状态。

实验过程

为了探究不同网络环境下的情况，作者在2016年11月和2017年4月分别进行了两次实验（第二次实验的网络负载较大），观测交易的产生并记录其提交所花费的时间。

为了充分收集包含在区块链中的交易信息，作者定义了观测窗口：从实验开始前的第一个区块到实验结束24h后的一个区块，这之间的交易即处于观测窗口中，都会被记录下来。

实验结果

• 无序到达对于提交时间的影响很大；
• 更低的手续费并不是造成orphan延迟提交的原因；
• 锁定时间也不是造成orphan延迟提交的关键因素。

---

以太坊交易的提交

在本节中，作者介绍了以太坊不能保证提交的原理，并实验研究了gas price、gas limit、network三个因素对提交时间的影响。

以太坊中交易事务的生命周期

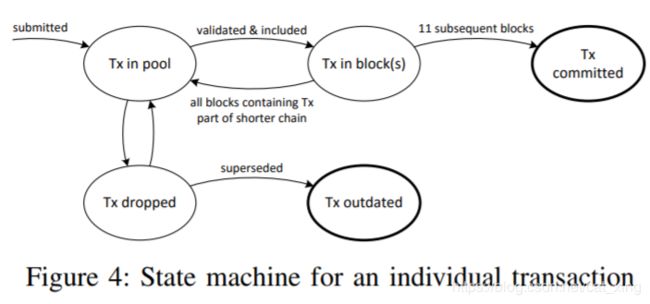
(i)交易发生并声明;
(ii)将该交易纳入某一链条上新开采的区块;
(iii)将交易纳入主链的区块部分;
(iv)其后链接了一定数量的区块后提交事务。
因为分叉现象或其他原因，步骤2并不能保证交易最终一定被提交，这就产生系统的可靠性问题。

实验过程

该实验研究交易从打包到最终提交所花费的时间以及分支合并后会丢失多少已打包的交易。作者改写了一个客户端节点作为监听节点，以检测交易声明和区块声明。
监听节点会记录交易声明的时间和区块到达的时间，以计算交易提交的延迟时间。

实验结果

• 交易数量越多，交易提交所花费的时间越长。
• gas price对于提交时间的影响有限，超过一定值后几乎不产任何影响。
• gas limit与提交时间并没有很大的联系。
• 由于每笔交易的有序性要求，网络延迟容易造成交易出现乱序，因此导致提交时间的增加。

---

BLOCK GAS LIMIT对以太坊的影响

gas limit通过限制每个区块消耗的gas总量防止DDoS攻击。如果交易所需的气体超过了限制值，交易就无法被包含到块中，这就使得大规模的分布式拒绝服务攻击难以发生。但是太小的gas limit也容易造成一些合约无法正常工作。

---

以太坊的交易终止机制

这部分作者将提出人工地中止交易的机制。该机制可用于提高软件客户端或者钱包的用户友好性。

• 如果用户想中止一个超过预期时间的交易，可发起一个接收者为自己的新的交易，新的交易与超时交易的编号一样，且交易金额为0，如果新的交易提交成功，超时交易将过期，如果超时交易在新的交易成功提交之前成功提交了，则与一开始的目的一样，没有任何问题。
• 用户也可以重新发起一次新的交易，新的交易包含与之前的交易一样的数据，但设置较高的手续费，因此新的交易的数字特征和哈希值与之前的交易不一样，可以被矿工认为是另一次交易。只要任何一个交易成功提交了，另外一个即过期了(因为nonce是一样的)，这样也可以达到终止的目的。

作者在3种场景下测试了以上的规则。

• 一笔交易在常规时间内没有被包含进区块中。
• 因为手续费不足，用户决定撤回之前发布的交易。
• 账户余额不足，交易无法被正常提交，因而无期限地等待。

均取得了很好的效果。

---

个人感悟

• 这是我看过的第一篇有关区块链的论文，但是里面有很多知识感觉很熟悉，跟分布式系统、计算机网络、信息安全等课程上的一些内容相似，也难怪，区块链的本质就是一个去中心化的分布式账本。
• 区块链的构成技术有：P2P技术、共识算法、密码学算法、Merkle树；应用的实例有：由日本Morgen银行和ripple等提供的快速，安全，便捷的国际转账服务、SWIFT自己正在建立的区块链网络，加速国际转账、IBM建立的supply chain，探索潜在服务、比特币
• 当前区块链技术可应用于许多场景，但是由于其现有机制的问题导致了数据提交的时候，需要耗费一定的时间，且提交的成功与否具有不确定性，造成了一定不便。因此可将如何缩短数据提交所需要的时间，以及提高成功提交的概率作为区块链技术研究的主要方向。

---

改进方案

当前的区块链系统，虽然系统中的使用硬件的算力已经比较高，但是处理能力仍然不足，不能够支撑计算密集的智能合约或者高频交易且容易受到Dos攻击的影响。所以未来可以考虑将从一下几个方面进一步提高系统可用性。

• 从区块链系统设计层面提高系统处理能力
• 改善等待机制提高提交成功率
• 添加完善真正应用所需的功能