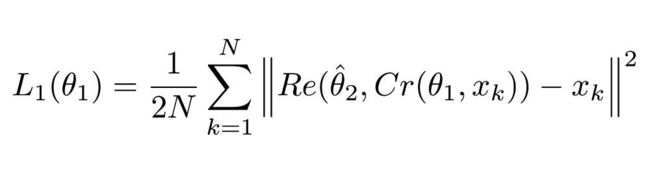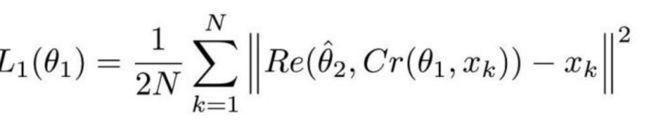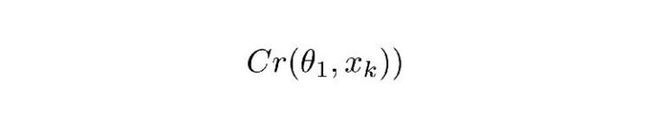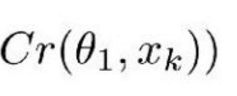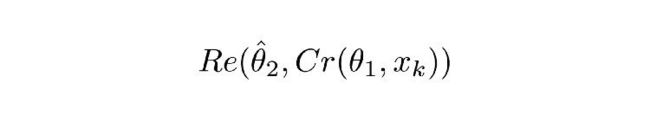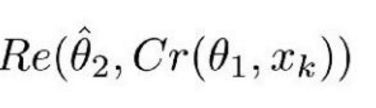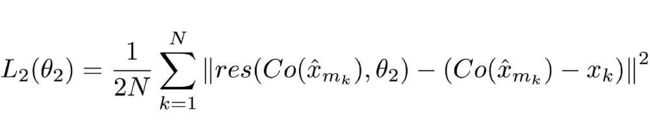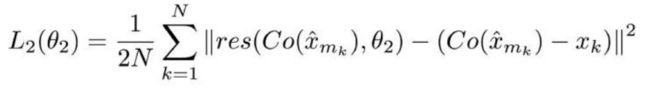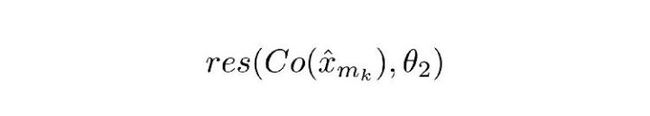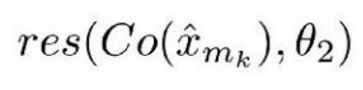基于深度学习的图像压缩

近年来，深度学习在计算机视觉领域已经占据主导地位，不论是在图像识别还是超分辨重现上，深度学习已成为图片研究的重要技术，但它们的能力并不仅限于这些任务；现在深度学习技术已进入图片压缩领域。下面就说说神经网络在图像压缩领域的应用。

当前主要图片压缩算法

说到图像压缩算法，目前市面上影响力比较大的图片压缩技术是WebP和BPG

WebP：谷歌在2010年推出的一款可以同时提供有损压缩和无损压缩的图片文件格式，其以VP8为编码内核，在2011年11月开始可以支持无损和透明色功能。目前facebook、Ebay等网站都已采用此图片格式。

BPG：知名程序员、ffmpeg和QEMU等项目作者Fabrice Bellard推出的图像格式，它以HEVC为编码内核，在相同体积下，BPG文件大小只有JPEG的一半。另外BPG还支持8位和16位通道等等。尽管BPG有很好的压缩效果，但是HEVC的专利费很高，所以目前的市场使用比较少。

就压缩效果来说，BPG更优于WebP，但是BPG采用的HEVC内核所带来的专利费，导致其无法在市场进行大范围使用。在这种情况下，运用深度学习来设计图片压缩算法就应运而生。
 

早在 2016 年的时候，谷歌的研究人员就提出了一种基于神经网络的全分辨率有损图像压缩法《Full Resolution Image Compression with Recurrent Neural Networks》（利用循环神经网络进行全分辨率图像压缩）。

此后也陆续出现了不少这方面的研究，比如去年的IEEE大会上，来自哈尔滨工业大学的一组研究人员联合提交了一篇论文《An End-to-End Compression Framework Based on Convolutional Neural Networks》（基于卷积神经网络的端到端压缩框架）。

 

他们在这篇论文中就提出了一种新的基于卷积神经网络的压缩框架，能够实现图像的高质量压缩。这个框架由两部分组成：一个 ComCNN 用于学习输入图像中最优的紧凑表示，然后编码图像，一个 RecCNN 用于重构出高质量的解码图像。下面集智就说说这篇论文中利用深度学习技术进行图像压缩的方法。

 

什么是图像压缩？

图像压缩就是转换图像的过程，让图像占据更少的空间。很多图像如果直接存储的话或占据很大的空间，所以出现了不少编解码器，比如 JPEG 和 PNG，目的就是减少原始图像的大小。

 

有损压缩 VS 无损压缩

目前有两种压缩形式：有损压缩和无损压缩。从名字上就能看出来，无损压缩能够恢复原始图像的全部数据，而有损压缩则在图像转换过程中会丢失一些数据。

 

比如，JPG 就是一种有损压缩算法，而 PNG 就是一种无损压缩算法。

 

 

图：无损压缩和有损压缩对比

 

注意右侧图像上有很多块状的类似马赛克的透明斑点，这就表示图像的信息丢失了。同一颜色的相邻像素会被压缩为一个区域以节省空间，但是也会导致实际像素丢失信息。当然了，像 JPEG，PNG 等这样的算法更复杂些，但上面这个例子应该能很直观地展示出了有损压缩。无损压缩很好，不过最终会在硬盘上占据大量空间。

 

还有一些更好的图片压缩方法，不会损失太多的图像信息，但是压缩速度很慢。不少还是使用迭代方法，意味着无法在多个 CPU 和 GPU 上并行运行。因而在日常生活中用起来不太实际。

 

引入卷积神经网络

如果有什么东西能够进行计算，还能近似实现，那就使用神经网络吧。在哈工大的这篇论文中，作者就使用了非常标准的卷积神经网络用来优化图像压缩。他们的方法不仅能很好地的完成图像压缩，而且还能应用并行计算，大幅提高了压缩速度。

 

这种方法背后的原理就是卷积神经网络非常善于从图像中提取空间信息，然后将信息表示为更复杂的形式（比如，只存储图像的“重要”比特）。作者想借助 CNN 的这种能力来更好地表示图像。

 

模型架构

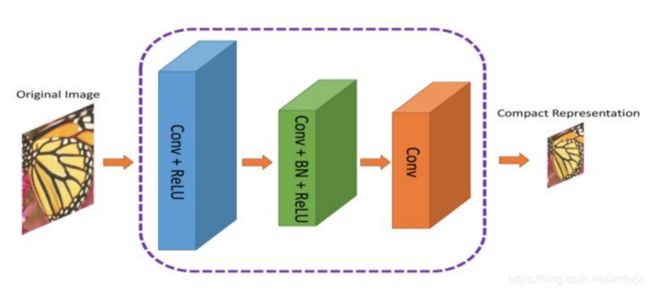
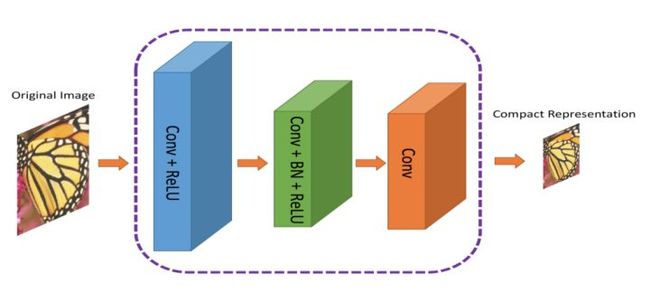
作者提出了一种双元网络架构，第一个网络会提取图像的信息并生成紧凑的表示（ComCNN），然后用一个标准的编解码器（比如 JPEG）处理该网络的输出结果。再通过编解码器处理后，图像会被传递到第二个神经网络，它会“修复”来自编解码器的图像，试图恢复原始图像的信息，这个网络被作者称为重构 CNN（RecCNN）。这两个网络都经过迭代训练，和 GAN 类似。

图：ComCNN模型架构。图像的紧凑表示通过它传入编解码器。

 

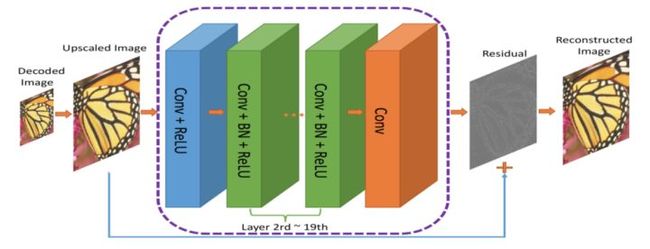
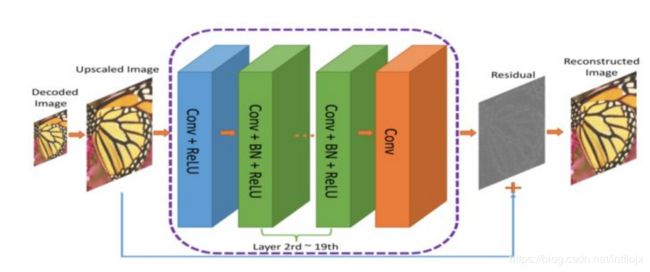
图：压缩图像的端到端框架。Co(.) 表示图像压缩算法；作者使用了JPEG，JPEG2000和BPG

 

编解码器的输出结果经过分辨率提高后，传输到 RecCNN 中。RecCNN 会输出一张最大限度与原始图像一致的照片。

 

什么是残差？

残差可以看作对编解码器解码出的图像进行“优化”的后期处理步骤。神经网络经过学习后，对图像有了丰富的认知，能够决定“修复”哪些东西。这里的理念基于深度残差学习。

 

损失函数

由于有两个神经网络，所以应用了两个损失函数。第一个是用于 ComCNN 网络的损失函数，定义为：

图：ComCNN的损失函数

 

解释

该等式看着很复杂，但实际上它就是个均方误差（MSE）。这里的||²表示它们封装进的向量的正则项。

图：公式1.1

 

Cr 表示 ComCNN 的输出结果。θ 表示 ComCNN 的可训练参数，Xk 表示输入图像。

 

Re() 表示 RecCNN，该公式只将公式 1.1 的值传入 RecCNN 中。估量符号 θ 表示 RecCNN 的可训练参数。

直观定义

公式 1.0 会让 ComCNN 修改其权重，从而使图像经过 RecCNN 重建之后，能尽可能地接近原始输入图像。

 

第二个是用于 RecCNN 的损失函数，定义如下：

解释

同样，这个损失函数看着也很复杂，但实际上仍是个标准的神经网络损失函数——MSE。

Co() 表示编解码器的输出结果，估量符号 x 表示 ComCNN 的输出，θ2 表示 RecCNN 的可训练参数。Res() 表示神经网络学习的残差，只是 RecCNN 的输出结果。值得一提的是，RecCNN 的训练基于 Co() 和输入图像，并非直接基于输入图像。

直观定义

公式 2.0 会让 RecCNN 修改其权重，让它的输出最大限度接近原始图像。

训练机制

模型以迭代的方式进行训练，和 GAN 模型的训练方式相同。其中一个模型的权重固定不变，只更新第二个模型的权重；然后让第二个模型的权重保持不变，只更新第一个模型的权重。

 

基准

论文作者将他们的方法和现存方法进行了比较，包括普通的编解码在内。最终证明他们的方法效果要优于其它方法，在保持较高的压缩速度的同时，图像的质量也得到了保证。

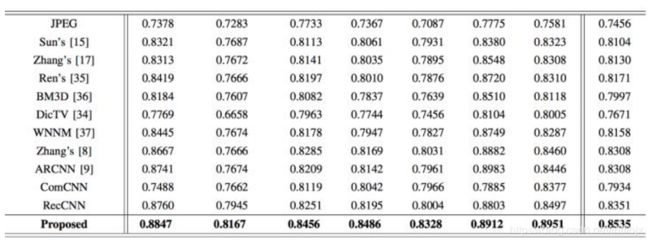
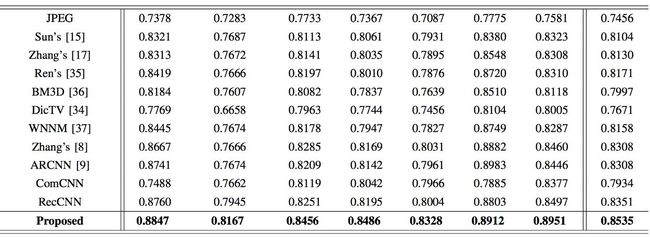
图：SSIM（结构相似度指数）比较。值越高表示和原图越相似。加粗值表示论文方法的结果。

 

结语

本篇论文向我们展示了深度学习技术在图像压缩领域的应用，不仅压缩效果比肩当前最先进的方法，而且具有更快的压缩速度。我们从中也可以看到深度神经网络在诸如图像分类和图像处理等常见任务以外的领域，同样大有可为。

 

除了本文讲解的这篇论文外，我们也收集了最近出现的一些相关研究成果，比如：

• 《DeepN-JPEG: A Deep Neural Network Favorable JPEG-based Image Compression Framework》（DeepN-JPEG：基于JPEG的深度神经网络图像压缩框架）

论文地址：

https://arxiv.org/pdf/1803.05788.pdf

 

• 《Deep Image Compression via End-to-End Learning》（通过端到端学习进行深度图像压缩）

论文地址：

https://arxiv.org/pdf/1806.01496.pdf

 

• 《Semantic Perceptual Image Compression using Deep Convolution Networks》（利用深度卷积神经网络进行语义感知图像压缩）

 

论文地址：

https://arxiv.org/abs/1612.08712

 

该论文的代码实现地址：

https://github.com/iamaaditya/image-compression-cnn

 

• 《Real-Time Adaptive Image Compression》（实时自适应图像压缩）
• https://arxiv.org/pdf/1705.05823.pdf