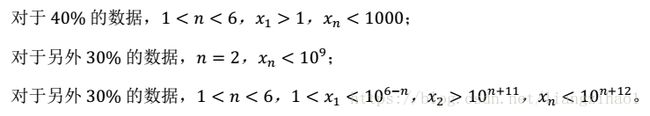jzoj 5864. 【NOIP2018模拟9.11】很多序列 数论

Description

Input

Output

Sample Input

2
4 7

Sample Output

17

Data Constraint

分析：
n=2 n = 2 就是noipD1T1，直接输出 x∗y−x−y x ∗ y − x − y 。
考虑 n>2 n > 2 怎么做，此时 x1<103 x 1 < 10 3 。
我们设 k=x1 k = x 1 ， a[i] a [ i ] 为在 mod k m o d   k 意义下，余数为 i i 的最小的能被表示的数是多少。
因为有 k k 这一个数，如果能表示出 a[i] a [ i ] ，那么 a[i]+k a [ i ] + k 也能被表示出，答案其实就是 (maxk−1i=0a[i])−k ( max i = 0 k − 1 a [ i ] ) − k 。
考虑怎样处理出 a a ，显然 a0=0 a 0 = 0 ，然后依次加入第 2 2 个到第 n n 个数。我们先把前 i−1 i − 1 个数得到的 i i 放进一个堆里，每次弹出一个 a[i] a [ i ] 最小的数，判断能否去更新 a[(i+d) mod k] a [ ( i + d )   m o d   k ] ，假设当前插入的是 d d ，如果能更新，就把这个新的也插入到堆里，这样就做完了。

代码：

#include 
#include 
#include 
#include 
#define LL long long

const int maxn=1e5+7;

using namespace std;

LL n;
LL a[10],h[maxn];

struct rec{
    LL x,k;
};

bool operator <(rec a,rec b)
{
    return a.x>b.x;
}

priority_queue  q;

int main()
{
    freopen("sequence.in","r",stdin);
    freopen("sequence.out","w",stdout);
    scanf("%lld",&n);
    for (LL i=1;i<=n;i++) scanf("%lld",&a[i]);
    if (n==2) printf("%lld",a[1]*a[2]-a[1]-a[2]);
    else
    {
        for (LL i=1;i1];i++) h[i]=1e18;
        for (LL i=2;i<=n;i++)
        {
            for (LL j=0;j1];j++) q.push((rec){h[j],j});
            while (!q.empty())
            {
                rec d=q.top();
                q.pop();
                LL k=d.k,l=(k+a[i])%a[1];
                if (h[l]>h[k]+a[i])
                {
                    h[l]=h[k]+a[i];
                    q.push((rec){h[l],l});
                }
            }
        }
        LL ans=0;
        for (LL i=0;i1];i++) ans=max(ans,h[i]-a[1]);
        printf("%lld",ans);
    }
}