洛谷P5021 赛道修建【树形DP+贪心】
时空限制 1000ms / 128MB
题目描述
C 城将要举办一系列的赛车比赛。在比赛前,需要在城内修建 m m m 条赛道。
C 城一共有 n n n 个路口,这些路口编号为 1 , 2 , … , n 1,2,…,n 1,2,…,n,有 n − 1 n-1 n−1 条适合于修建赛道的双向通行的道路,每条道路连接着两个路口。其中,第 i i i 条道路连接的两个路口编号为 a i a_i ai 和 b i b_i bi,该道路的长度为 l i l_i li。借助这 n − 1 n-1 n−1 条道路,从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路 e 1 , e 2 , … , e k e_1,e_2,…,e_k e1,e2,…,ek,满足可以从某个路口出发,依次经过 道路 e 1 , e 2 , … , e k e_1,e_2,…,e_k e1,e2,…,ek(每条道路经过一次,不允许调头)到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全,要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案,使得修建的 m m m 条赛道中长度最小的赛道长度最大(即 m m m 条赛道中最短赛道的长度尽可能大)
输入格式
输入文件第一行包含两个由空格分隔的正整数 n , m n,m n,m,分别表示路口数及需要修建的 赛道数。
接下来 n − 1 n-1 n−1 行,第 i i i 行包含三个正整数 a i , b i , l i a_i,b_i,l_i ai,bi,li,表示第 i i i 条适合于修建赛道的道 路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 n − 1 n-1 n−1 条道路相互到达。每行中相邻两数之间均由一个空格分隔。
输出格式
输出共一行,包含一个整数,表示长度最小的赛道长度的最大值。=
【数据规模与约定】
所有测试数据的范围和特点如下表所示 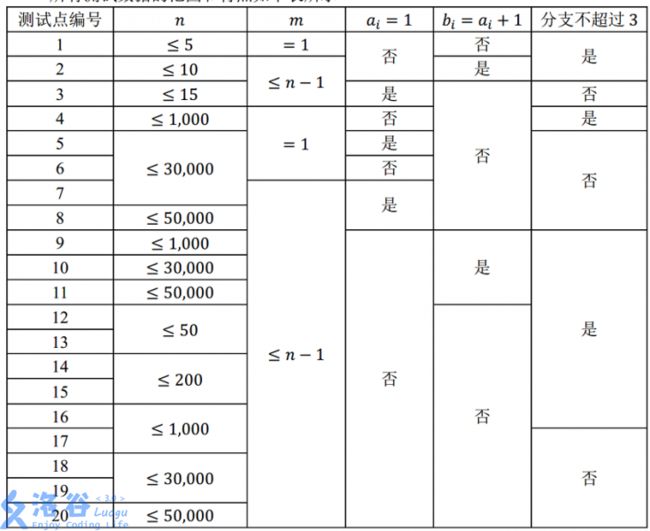
其中,“分支不超过 3 3 3”的含义为:每个路口至多有 3 3 3 条道路与其相连。 对于所有的数据, 2 ≤ n ≤ 50 , 000 2 ≤ n ≤ 50,000 2≤n≤50,000, 1 ≤ m ≤ n − 1 1 ≤ m ≤ n-1 1≤m≤n−1, 1 ≤ a i , b i ≤ n 1 ≤ a_i,b_i ≤ n 1≤ai,bi≤n, 1 ≤ l i ≤ 10 , 000 1 ≤ l_i ≤ 10,000 1≤li≤10,000。
题目分析
noip2018考场上的我菜得抠jio,只拿了m=1和链的部分分,现在再看。。
二分最小长度mid判断肯定不用说
我们记从当前结点 u u u出发到其每个子树内的最长路径为 d i s v i dis_{v_i} disvi,这些值分为两种情况
1. d i s v i ≥ m i d dis_{v_i}\geq mid disvi≥mid,直接加入到答案贡献内
2.剩下的值两两配对存在 d i s v i + d i s v j ≥ m i d dis_{v_i}+dis_{v_j}\geq mid disvi+disvj≥mid,这种情况下要尽量多的配对累加对答案的贡献,最后不能配对的值中向上传递最大的一个
这个就是贪心的思想,假如u的子树内当前能配对而不配对
由于u到其父亲的边只能用一次,向上传递后最多只能产生1的贡献了
这些值可以用multiset维护,维护配对过程要尽量减少对stl的操作,否则可能T
蒟蒻前面因为配对的扫描方法多了个删除操作T了好几发
// luogu-judger-enable-o2
#include::iterator
int read()
{
int f=1,x=0;
char ss=getchar();
while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();}
while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();}
return f*x;
}
const int maxn=100010;
int n,m;
struct node{int v,dis,nxt;}E[maxn<<1];
int head[maxn],tot,res;
multiset<int> st[maxn];
void add(int u,int v,int dis)
{
E[++tot].nxt=head[u];
E[tot].v=v; E[tot].dis=dis;
head[u]=tot;
}
int DP(int u,int pa,int x)
{
st[u].clear();
for(int i=head[u];i;i=E[i].nxt)
{
int v=E[i].v;
if(v==pa) continue;
int len=DP(v,u,x)+E[i].dis;
if(len>=x) res++;
else st[u].insert(len);
}
for(IT it=st[u].begin();it != st[u].end();)
{
IT tt=st[u].lower_bound(x-*(it));
if(tt!=st[u].end())
{
if(tt==it)
{
tt++;
if(tt==st[u].end()){ it++; continue;}
}
res++;
st[u].erase(tt);
st[u].erase(it++);
}
else it++;
}
if(!st[u].empty())
{
IT tt=st[u].end();
tt--; return *tt;
}
return 0;
}
int check(int x)
{
res=0; DP(1,0,x);
return res>=m;
}
int main()
{
n=read();m=read();int sum=0;
for(int i=1;i<n;++i)
{
int u=read(),v=read(),dis=read();
add(u,v,dis); add(v,u,dis); sum+=dis;
}
int L=0,R=sum+1,ans;
while(L<R)
{
int mid=L+R>>1;
if(check(mid)) L=mid+1,ans=mid;
else R=mid;
}
printf("%d",ans);
return 0;
}