变分自编码器VAE(Variational Autoencoders)及示例代码

这里写一个中文版快速入门笔记，更细致的理论分析和推导见：
Tutorial on Variational Autoencoders

VAE是一个学习复杂分布的无监督学习模型。在实践中，给定数据$X$，我们往往想得到$P(X)$，使得那些真实数据概率较大，而随机噪声概率较小。同时，我们还希望能够生成更多其他类似“真实”的例子，进而丰富我们的数据，典型例子如动画设计等领域，这就是“生成”模型的motivation。

形式化的表述为：已知数据$X$是从某未知真实数据分布$P_{gt}(X)$采样而来，我们的目标是学习一个可采样模型$P$，且$P$和$P_{gt}(X)$尽可能相似。

潜变量模型

真实数据$X$可能是高维的，并且依赖关系复杂，潜变量模型将问题按步骤分解：首先假设有一潜变量$z\in Z$，$Z$是隐空间，易于根据概率密度函数$P(z)$采样；其次，假定有一族函数$X^{\prime }=f(z;\theta )$，将$z$映射为数据$X^{\prime }$。其中，$z$为随机变量，$\theta$为固定参数，$X^{\prime }$为与真实数据$X$类似的"新"数据。

学习的目的就是要优化$\theta$，目标为最大化真实数据$X$的概率：
$$P(X)=\int P(X|z;\theta )P(z)dz$$其中$P(X|z;\theta )=N(X|f(z,\theta ),{\sigma }^2\ast I)$

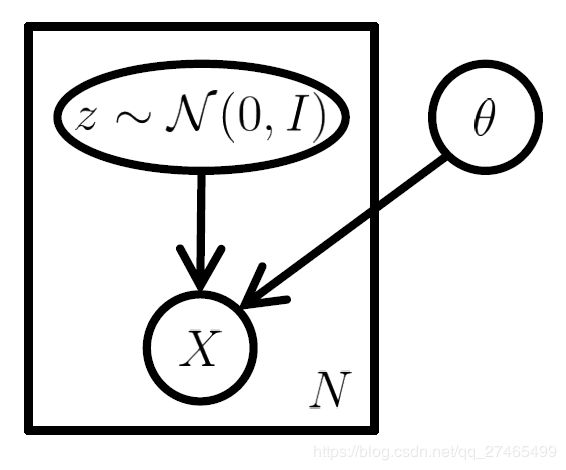
注意到生成分布选择的是Guass分布。其他分布也可以，但需要满足：$P(X|z;\theta )$可计算且在$\theta$处连续，可通过梯度下降进行优化。
当不使用潜变量生成模型，直接取确定性的$X^{\prime }=f(z;\theta )$时，相当于生成分布是一个Dirac delta分布，在$\theta$上不连续。此时模型就是传统自编码器模型，它是点对点的，可以进行压缩降维，但不具备直接生成功能（其他未知的$z^{\prime }$对应的$X^{\prime }$是什么完全不清楚）。实际上，变分自编码器和传统自编码器只是在网络结构上有一定的相似之处，但本质完全不同。

变分自编码器

在潜变量模型的基础上，还需处理两个问题：

1. $P(z)$的选择，事实上，任意$d$维分布都可由$d$个正态分布的变量通过足够复杂的函数映射而成，只需取$P(z)=N(0,I)$即可，进一步的说明可参见原文。
2. 将上面的优化目标$P(X)$转化为可计算梯度的Loss Function，这就用到变分自编码器的另一个核心方法——变分法。

考虑直接使用蒙特卡洛方法：$P(X)\approx \frac{1}{n}{\sum }_{i}P(X|z_i)$，有两个弊端：1) 复杂的问题对于采样的样本量需求过大；2) 高斯分布设定下的极大似然度量等价于欧式平方距离，不满足复杂任务需求，对于这一点我们在文末给予详细讨论。
VAE通过改变采样过程同时解决以上两个弊端。

设定优化目标

事实上，大多数潜变量$z$对于生成$X$没有贡献，也就是说，$P(X|z)\approx 0$。VAE的核心思想就是，尽量只采样那些对生成$X$有贡献的$z$，然后根据其估计$P(X)$。
于是，我们需要一个新的函数$Q(z|X)$(近似后验分布)，估计可能生成$X$的$z$的分布，希望以此减小$z$的采样空间，这样我们就可以轻松地通过
$$P(X)\approx E_{z\sim Q}P(X|z)$$来估计$P(X)$。

接下来，要最大化$P(X)$，就需要对$Q$有所约束。约束从哪里来？
固定$X$，对于任意$Q(z|X)$，我们希望其接近真实后验分布$P(z|X)$，考察其KL散度:
$$D[Q(z|X)||P(z|X)]=E_{z\sim Q}[\log Q(z|X)-\log P(z|X)]$$对上式使用贝叶斯规则：
$$D[Q(z|X)||P(z|X)]=E_{z\sim Q}[\log Q(z|X)-\log P(X|z)-\log P(z)]+\log P(X)$$变形得到：
$$\log P(X)-D[Q(z|X|)||P(z|X)]=E_{z\sim Q}[\log P(X|z)]-D[Q(z|X)||P(z)]$$上式就是VAE的核心：左侧是我们的优化目标，称之为变分下界——最大化$P(X)$，最小化$Q$模拟真实后验分布的误差；右侧是我们的计算形式——当选择合适的$Q$时，就可以计算梯度并使用SGD进行优化（意味着$Q$和$P(z)$都必须是连续分布）。右侧在形式上接近自编码器：$Q$将$X$编码为$z$，$P$将$z$解码为$X$。该方法还有一个额外的好处，在优化过程中，只要选取一个高容量的$Q$，那么左侧第二项就会尽可能的减小，我们可以直接使用$Q(z|X)$代替$P(z|X)$。

优化方法

通常取$Q(z|X)=N(z|\mu (X),\Sigma (X))$，其中$\mu$和$\Sigma$都通过神经网络实现，则$D[Q(z|X)||P(z)]$是两个多元高斯分布之间的KL散度：
$$D(N({\mu }_0,{\Sigma }_0)||N({\mu }_1,{\Sigma }_1))=\frac{1}{2}\left(tr\right({\Sigma }_1^{-1}{\Sigma }_0)+({\mu }_1-{\mu }_0{)}^T{\Sigma }_1^{-1}({\mu }_1-{\mu }_0)-k+\log \left(\frac{\det {\Sigma }_1}{\det {\Sigma }_0}\right))$$其中$k$是分布的维度。
在当前设定下可简化为：
$$D(N(\mu (X),\Sigma (X))||N(0,I))=\frac{1}{2}\left(tr\right(\Sigma (X))+(\mu (X){)}^T(\mu (X))-k-\log \det (\Sigma (X)))$$接下来我们就可以使用SGD来进行优化。
还存在的一个技术性问题是：$E_{z\sim Q}[\log P(X|z)]$同时依赖$P$和$Q$的参数，如下图左侧所示：

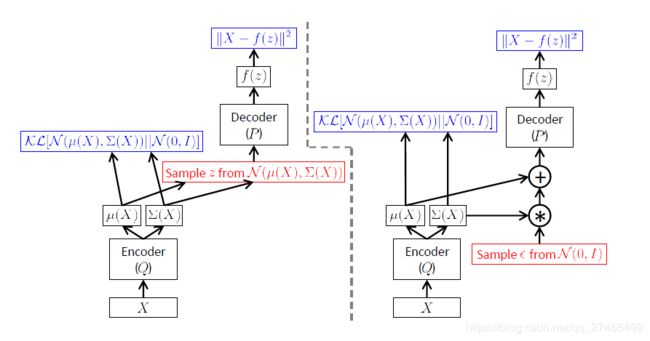
在BP的过程中，误差需要穿过一个采样层，该操作不连续且没有梯度。SGD可以处理随机输入，但不能处理随机操作！解决方法称为“重新参数化”，如上图右侧所示。先采样$ϵ\sim N(0,1)$，然后令$z=\mu (X)+{\Sigma }^{1/2}(X)\ast ϵ$。则实际要优化的函数为：
$$E_{X\sim D}\left[E_{ϵ\sim N(0,1)}\right[\log |P(X|z=\mu (X)+{\Sigma }^{1/2}(X)\ast ϵ)]-D(Q(z|X)||P(z))]$$

生成&测试

生成新样本时，直接从$z$的先验分布$N(0,I)$采样生成新样本即可。此外，通过从$Q$中采样可得到新样本生成概率的良好估计。

讨论

毫无疑问，对于固定的“解码器”$P$，如果$P(z|X)$不是高斯分布，则$D[Q(z|X|)||P(z|X)]$永远不可能为0，我们只能得到$\log P(X)$的一个下界。是否存在函数$f$能够最大化$\log P(X)$同时使得$P(z|X)$对任意$X$都是高斯分布？仍然是一个开放问题。某些简单情形已经得到证明。

从信息论的“最小描述长度”理论也可以对VAE进行解释：
$\log P(X)$：当前模型对X完全理想编码所需bit
$D[Q(z|X|)||P(z|X)]$：当前编码是次优编码，未能包含生成x的所有信息，这部分需要减去
$E_{z\sim Q}[\log P(X|z)]$：从$z$生成$X$编码所需bit
$D[Q(z|X)||P(z)]$：使用后验分布而不是先验分布所带来的额外信息量，需要减去

条件变分自编码器（CVAE）

将上述VAE推广到多模态，优化目标从$P(Y)$变成$P(Y|X)$（这里对X,Y进行了重新定义）

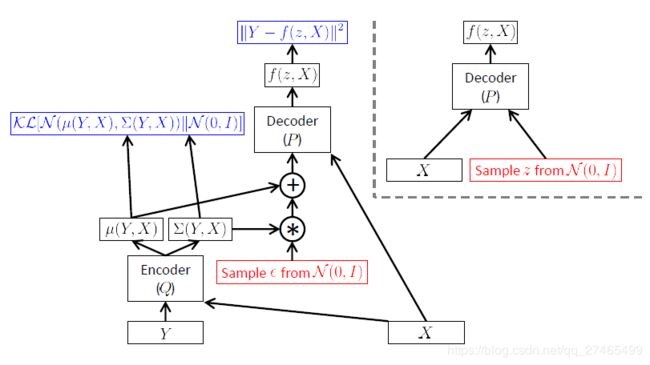
关于相似性度量

一句话，相似性度量决定了生成模型在生成新样本时，新样本与原样本微小差异的方向。
例如简单的潜变量模型，采用平方距离度量，在生成新样本时，就倾向于产生与原样本具有较小平方距离的新样本。如下图所示，a为原样本，b c为新样本，b与a的平方距离更小（c是a的图像整体平移得到的）。在生成过程中，简单的潜变量模型就更倾向于生成b而不是c。这与我们的直观印象是相悖的，往往需要根据经验和具体问题来人为设计相似性度量。

VAE是如何解决这个问题的？VAE给直接采样过程加入了新的信息，就是模拟后验分布$Q(z|X)$，生成样本的时候就不是在潜变量$z$的整个空间采样(通过$P(z)$)，而是在其子空间（通过$Q(z|X)$）采样，从模型的解释性上来说，潜变量$z$存储的就是类似于数字，角度，位置，线条粗细，风格等类似的一系列潜在因素。从优化目标来看，要同时最大化$\log P(X)$和最小化$D[Q(z|X)||P(z|X)]$，对子空间的精确限制就是在避免(b)这种不合理清形的出现。另一方面，从优化目标的计算形式来看（虽然不是非常精确，但也能窥到一些端倪），要同时最小化平方距离和$D[Q(z|X)||P(z)]$，也就是说既要新样本在平方距离上接近，同时也要潜空间上引入的信息量更小。对于样本b来说，虽然平方距离上接近，但是要生成这样的样本，潜空间上的决定因素和a差异很大，而c在潜空间上和a的一致性更高。从而，VAE更倾向于生成c而非b。

总之，简单的潜变量模型对$z$所在因素空间的划分是只以平方距离为导向的、平均化的、混乱的，使得非a所属子因素空间内的$z$强行生成，最后得到了b。而VAE为每个样本划分了专属的子因素空间，使得各自子因素空间内的$z$只致力于生成对应的$X^{\prime }$，同时$D[Q(z|X)||P(z|X)]$的优化约束保证了子因素空间划分的合理性。

总结

1. AE是点对点模型，生成没有任何数学保证；
2. 潜变量模型强行用其他潜因素生成目标，只保证平方距离小，风格差异大；
3. VAE优化目标左侧，既要生成概率大，又要模拟后验分布精准（潜空间合理划分）
4. VAE优化目标右侧，b平方loss小而$D[Q(z|X)||P(z)]$loss大，c平方loss大而$D[Q(z|X)||P(z)]$loss小。

一个简单的VAE代码：

import tensorflow as tf

class VariationalAutoencoder(object):

    def __init__(self, n_input, n_hidden, optimizer = tf.train.AdamOptimizer()):
        self.n_input = n_input
        self.n_hidden = n_hidden

        network_weights = self._initialize_weights()
        self.weights = network_weights

        # model
        self.x = tf.placeholder(tf.float32, [None, self.n_input])
        self.z_mean = tf.add(tf.matmul(self.x, self.weights['w1']), self.weights['b1'])
        self.z_log_sigma_sq = tf.add(tf.matmul(self.x, self.weights['log_sigma_w1']), self.weights['log_sigma_b1'])

        # sample from gaussian distribution
        eps = tf.random_normal(tf.stack([tf.shape(self.x)[0], self.n_hidden]), 0, 1, dtype = tf.float32)
        self.z = tf.add(self.z_mean, tf.multiply(tf.sqrt(tf.exp(self.z_log_sigma_sq)), eps))

        self.reconstruction = tf.add(tf.matmul(self.z, self.weights['w2']), self.weights['b2'])

        # cost
        reconstr_loss = 0.5 * tf.reduce_sum(tf.pow(tf.subtract(self.reconstruction, self.x), 2.0))
        latent_loss = -0.5 * tf.reduce_sum(1 + self.z_log_sigma_sq
                                           - tf.square(self.z_mean)
                                           - tf.exp(self.z_log_sigma_sq), 1)
        self.cost = tf.reduce_mean(reconstr_loss + latent_loss)
        self.optimizer = optimizer.minimize(self.cost)

        init = tf.global_variables_initializer()
        self.sess = tf.Session()
        self.sess.run(init)

    def _initialize_weights(self):
        all_weights = dict()
        all_weights['w1'] = tf.get_variable("w1", shape=[self.n_input, self.n_hidden],
            initializer=tf.contrib.layers.xavier_initializer())
        all_weights['log_sigma_w1'] = tf.get_variable("log_sigma_w1", shape=[self.n_input, self.n_hidden],
            initializer=tf.contrib.layers.xavier_initializer())
        all_weights['b1'] = tf.Variable(tf.zeros([self.n_hidden], dtype=tf.float32))
        all_weights['log_sigma_b1'] = tf.Variable(tf.zeros([self.n_hidden], dtype=tf.float32))
        all_weights['w2'] = tf.Variable(tf.zeros([self.n_hidden, self.n_input], dtype=tf.float32))
        all_weights['b2'] = tf.Variable(tf.zeros([self.n_input], dtype=tf.float32))
        return all_weights

    def partial_fit(self, X):
        cost, opt = self.sess.run((self.cost, self.optimizer), feed_dict={self.x: X})
        return cost

    def calc_total_cost(self, X):
        return self.sess.run(self.cost, feed_dict = {self.x: X})

    def transform(self, X):
        return self.sess.run(self.z_mean, feed_dict={self.x: X})

    def generate(self, hidden = None):
        if hidden is None:
            hidden = self.sess.run(tf.random_normal([1, self.n_hidden]))
        return self.sess.run(self.reconstruction, feed_dict={self.z: hidden})

    def reconstruct(self, X):
        return self.sess.run(self.reconstruction, feed_dict={self.x: X})

    def getWeights(self):
        return self.sess.run(self.weights['w1'])

    def getBiases(self):
        return self.sess.run(self.weights['b1'])