【计算机图形学】流体模拟渲染基础

流体模拟渲染基础

• 前言
• 矢量微积分
• Naiver-Stokes偏微分方程组
• N-S方程的分步求解
• 对流算法

前言

  本文主要参考文献《FLUID SIMULATION SIGGRAPH 2007 Course Notes》，结合我的理解单纯地讲述一下流体渲染的一些基础知识，本人水平有限，如有错误，欢迎指出。本文只是单纯针对流体模拟领域，可能一些地方不太严谨，但是对于虚拟模拟来说是可行的。即便如此，本文涉及到大量的数学方法。

一、矢量微积分

  高等数学中太多数讨论的是一维的微积分，而矢量微积分则是一维微积分的高维扩展。矢量微积分的三个基础算子：梯度（符号为$\nabla$），散度（符号为$\nabla \cdot$)，旋度（符号为$\nabla \times$），在此基础上流体力学中经常用到的还有拉普拉斯算子。

1、梯度（Gradient）

  梯度实际上就是矢量的空间偏导数，且结果依然是一个矢量，$2$维的梯度如下：
$$\nabla f(x,y)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\text{\hspace{1em}(1.1)}$$
  依此类推，$3$维的梯度有如下形式：
$$\nabla f(x,y,z)=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})\text{\hspace{1em}(1.2)}$$
  有时也会采用如下形式来表示梯度：
$$\nabla f=\frac{\partial f}{\partial x}\text{\hspace{1em}(1.3)}$$
  梯度通常用来近似计算函数值（实际上就是一维形式的推广)：
$$f(x+\Delta x)\approx f(x)+\nabla f(x)\cdot \Delta x\text{\hspace{1em}(1.4)}$$
  同样的，多个函数的梯度就构成了一个矩阵：
$$\nabla F=\nabla (f,g,h)=\left(\begin{array}{ccc}\frac{\partial f}{\partial x}& \frac{\partial f}{\partial y}& \frac{\partial f}{\partial z}\\ \frac{\partial g}{\partial x}& \frac{\partial g}{\partial y}& \frac{\partial g}{\partial z}\\ \frac{\partial h}{\partial x}& \frac{\partial h}{\partial y}& \frac{\partial h}{\partial z}\end{array}\right)=\left(\begin{array}{c}\nabla f\\ \nabla g\\ \nabla h\end{array}\right)\text{\hspace{1em}(1.5)}$$

2、散度（Divergence）

  散度算子仅仅应用于向量场，它衡量在某一点出相应的矢量聚集或者发散程度，测量方向为径向，结果为标量。$2$维、$3$维形式的散度算子如下所示：
$$\nabla \cdot u=\nabla \cdot (u,v)=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}$$

$$\nabla \cdot u=\nabla \cdot (u,v,w)=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\text{\hspace{1em}(1.6)}$$

  输入是矢量，而输出为标量。类比梯度，散度符号$\nabla \cdot u$可以理解为梯度$\nabla$与矢量$u$的点乘：
$$\nabla \cdot u=(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z})\cdot (u,v,w)=\frac{\partial }{\partial x}u+\frac{\partial }{\partial y}v+\frac{\partial }{\partial z}w\text{\hspace{1em}(1.7)}$$
  若矢量场散度为$0$，则称该矢量场无散度。

3、旋度（Curl）

  旋度衡量围绕某一点的旋转速度，测量方向为切向，三维形式的旋度是一个向量：
$$\nabla \times u=\nabla \times (u,v,w)=(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z},\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x},\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y})\text{\hspace{1em}(1.8)}$$
  倒推到$2$维，我们取上式中的$w=0$，即矢量场为$(u,v,0)$，$2$维向量场的旋度是一个标量：
$$\nabla \times u=\nabla \times (u,v)=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\text{\hspace{1em}(1.9)}$$
  同样地，旋度符号$\nabla \times u$我们可以理解为梯度$\nabla$与矢量场$u$的叉乘：
$$\nabla \times u=(\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z})\times (u,v,w)\text{\hspace{1em}(1.10)}$$
  若矢量场旋度为$0$，则称该矢量场无旋度。

4、拉普拉斯算子（Laplacian）

  拉普拉斯算子定义为梯度的散度，符号表示为$\nabla \cdot \nabla$，显然$\nabla \cdot$是散度，而后面的$\nabla$则为梯度，故拉普拉斯算子即梯度的散度，是一个二阶微分算子。$2$维、$3$维形式分别如下：
$$\nabla \cdot \nabla f=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}$$

$$\nabla \cdot \nabla f=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}+\frac{{\partial }^{2}f}{\partial z^2}\text{\hspace{1em}(1.11)}$$

  简言之，拉普拉斯算子定义如下：
$$\nabla \cdot \nabla f={\Sigma }_{i=1}^n\frac{{\partial }^{2}f}{\partial x_i^2}\text{\hspace{1em}(1.12)}$$
  偏微分方程$\nabla \cdot \nabla f=0$被称为拉普拉斯方程；而如果右边为某个非$0$常数，即$\nabla \cdot \nabla f=q$，我们称之为泊松方程。更一般地，如果梯度再乘上一个标量$a$（如$1/\rho$)，即$\nabla \cdot (a\nabla f)=q$，我们依旧称之为泊松问题。

二、$Naiver-Stokes$偏微分方程组

  流体模拟器的构建主要围绕著名的不可压缩$Navier-Stokes$方程展开，它是一个流体力学领域的偏微分方程，方程形式如下：
$$\frac{\partial u}{\partial t}+u\cdot \nabla u+\frac{1}{\rho }\nabla p=g+\nu \nabla \cdot \nabla u\text{\hspace{1em}(2.1)}$$

$$\nabla \cdot u=0\text{\hspace{1em}(2.2)}$$

  这个方程组看起非常地复杂，接下来我们就把它剖析成一个个比较简单的部分来理解。

1、符号标记

  我们有必要定义一些物理量的符号用以标记：

  符号$u$在流体力学中通常表示为流体的速度矢量，记$3$维的速度矢量$u=(u,v,w)$；

  希腊字符$\rho$是流体的密度，对于水，该值大约为$1000kg/m^3$，而空气则大约为$1.3kg/m^3$；

  字符$p$代表压力，流体对任何物体施加的单位面积力；

  字符$g$则是我们熟悉的重力加速度，通常取$(0,-9.81,0)m/s^2$。我们约定$y$轴向上，而$x$轴和$z$轴在水平面上。另外补充一点，我们把其他的一些类似的力都累加到$g$上，也就是我们统一用$g$表示所有类似力之和，这类力我们称之为体积力（称之为体积力是因为它们的力是作用到整个流体而不只是流体的表面）；

  希腊字符$\nu$是流体的运动粘度，它衡量流体的黏滞性。糖蜜之类的流体有非常高的粘度，而像酒精之类的流体有很低的粘度；

  其它一些矢量微积分的符号算子前面已经提到过，不再赘述。

2、动量方程

  偏微分方程$(2.1)$我们称之为动量方程，它本质上就是我们熟悉的牛顿定律$F=ma$的形式，描述了施加在流体上的力是如何影响流体的运动。

  假设我们用粒子系统来模拟流体，每个粒子代表流体的一小滴，每个粒子有各自的质量$m$、体积$V$和速度$u$。为了让整个粒子系统运作起来，我们必须弄清楚每个粒子所承受的力的作用。牛顿第二定律告诉我们：$F=ma$，而根据加速度定义，我们有：
$$a=\frac{Du}{Dt}\text{\hspace{1em}(2.3)}$$
  符号$D$是指物质导数，所谓物质导数，就是对流体质点求导数，而且是针对流体质点（在这里就是流体粒子）而不是空间的固定点。因而牛顿第二定律就变成：
$$m\frac{Du}{Dt}=F\text{\hspace{1em}(2.4)}$$
  那么流体粒子承受的力有哪些呢？一个最简单的力就是重力：$mg$。而其他的流体质点（或其他流体粒子）也会对当前的流体粒子产生作用力。流体内部的相互作用力之一便是压力，较大压力的区域会向较低压力区域产生作用力。值得注意的是，我们只关注施加在粒子上的压力的净合力。例如，若施加在粒子上压力在每个方向上都相等，那么它的压力的合力便为0。我们用压力的负梯度（取负是因为方向是由压力大的区域指向压力小的区域）来衡量在当前流体粒子处压力的不平衡性，即取$-\nabla p$。那么流体粒子所承受的压力就是对$-\nabla p$在整个流体粒子的体积上进行积分，为了简化，我们简单地将$V$与$-\nabla p$相乘，故粒子压力部分为$-V\nabla p$。

  其他的流体相互作用力则是由流体的黏性产生的，我们直观地把这种力理解为尽可能使得粒子以周围区域的平均速度移动的力，也就是使得粒子的速度与周围区域粒子速度的差距最小化。拉普拉斯算子是衡量一个量与之周围区域该量平均值之差的算符，因而$\nabla \cdot \nabla u$是当前粒子速度矢量与周围区域平均速度矢量之差。为了计算粘滞力，我们同样对$\nabla \cdot \nabla u$在整个粒子体积$V$上进行积分，与前面类似，我们简单取$V\nabla \cdot \nabla u$。除此之外，我们还引进一个称为动力粘度系数的物理量，符号为$\mu$。因而粘滞力为$V\mu \nabla \cdot \nabla u$。

  把重力、压力和粘滞力综合一起，我们可得：
$$m\frac{Du}{Dt}=F=mg-V\nabla p+V\mu \nabla \cdot \nabla u\text{\hspace{1em}(2.5)}$$
  当粒子系统中的粒子数量趋于无穷大，而每个粒子大小趋于$0$时，会产生一个问题：此时每个粒子的质量$m$和体积$V$变为$0$，此时上式变得没有意义。为此，我们把$(2.5)$式调整一下，两边同除以体积$V$，又因$\rho =m/V$，故有：
$$\rho \frac{Du}{Dt}=\rho g-\nabla p+\mu \nabla \cdot \nabla u\text{\hspace{1em}(2.6)}$$
  两边同除以$\rho$，移项调整：
$$\frac{Du}{Dt}+\frac{1}{\rho }\nabla p=g+\frac{\mu }{\rho }\nabla \cdot \nabla u\text{\hspace{1em}(2.7)}$$
  为了进一步简化，定义运动粘度为$\nu =\mu /\rho$，式$(2.7)$变为：
$$\frac{Du}{Dt}+\frac{1}{\rho }\nabla p=g+\nu \nabla \cdot \nabla u\text{\hspace{1em}(2.8)}$$
  我们已经快把动量方程推导出来，现在我们要把物质导数$\frac{Du}{Dt}$弄清楚，为此，我们需要了解两种描述方法：拉格朗日描述和欧拉描述。

3、拉格朗日描述与欧拉描述

  当我们尝试研究流体或可变形固体的运动的时候，通常有两种方法来描述：拉格朗日描述（ Lagrangian viewpoint）、欧拉描述（Eulerian viewpoint）。

  拉格朗日描述方法是我们比较熟悉的方法，这种描述方法把物体看成是由类似于粒子系统的形式组成，固体或流体的每个点看作一个独立的粒子，粒子有各自相应的位置$x$和速度$u$。我们可以把粒子理解为组成物体的分子。对于我们通常采用拉格朗日描述法进行建模模拟，即用一系列离散的粒子集来构建，粒子之间通过网格相联系。

  欧拉描述方法则采用了完全不同的角度，它常被用于流体力学中。与拉格朗日描述追踪每个物体粒子的方法不同，欧拉描述关注点是空间中的一个固定点，并考察在这个固定点上流体性质（如密度、速度、温度等）是如何随着时间变化的。流体流动经过这个固定点可能会导致这个固定点的物理性质发生一些变化（如一个温度较高的流体粒子流经这个固定点，后面紧跟着一个温度较低的流体粒子流过固定点，那么这个固定点的温度会降低，但是并没有任何一个流体粒子的温度发生了变化）。

  用天气测量举个简单的例子：拉格朗日描述方法就是你乘坐在一个随风而飘的热气球上，测量周围空气的压力、密度和浑浊度等天气指标；而欧拉描述方法就是你固定在地面上，测量流过的空气的天气指标。

  欧拉描述法似乎看起来带来了一些不必要的复杂度，但是目前大多数的流体模拟器都是基于欧拉描述法，这是因为欧拉描述法相比于拉格朗日描述法有一些不可比拟的优点：欧拉描述法能够更加方便地计算一些物理量的空间导数（例如压力梯度和粘度）；而如果用粒子方法的话（即拉格朗日描述法），那么计算物理量相对于空间位置的变化是比较难的。

  把拉格朗日描述法和欧拉描述法联系起来的关键点就是物质导数。首先从拉格朗日描述法出发，假设有一群粒子，每个粒子都有各自的位置$x$和速度$u$。记$q$为通用的物理量（如密度、速度和温度等），每个粒子有其对应的$q$值。方程$q(t,x)$描述在时间点$t$而位置为$x$的粒子对应的物理量值$q$。则一个粒子的物理量$q$随时间$t$的变化率是多少？这是一个拉格朗日描述角度下的问题，我们取对时间$t$的导数（注意用到了求导链式法则，以及$\frac{\partial q}{\partial x}=\nabla q$和$u=\frac{dx}{dt}）$：
$$\frac{d}{dt}q(t,x)=\frac{\partial q}{\partial t}+\nabla q\cdot \frac{dx}{dt}=\frac{\partial q}{\partial t}+\nabla q\cdot u\equiv \frac{Dq}{Dt}\text{\hspace{1em}(2.9)}$$
  这就是物质导数。把式$(2.9)$代入式$(2.8)$我们就得到了流体动量方程$(2.1)$。物质导数针对的是流体质点（在这里就是流体粒子）而不是空间的固定点。式$(2.9)$写完整一点就是：
$$\frac{Dq}{Dt}=\frac{\partial q}{\partial t}+u\frac{\partial q}{\partial x}+v\frac{\partial q}{\partial y}+w\frac{\partial q}{\partial z}\text{\hspace{1em}(2.10)}$$
  对于给定的速度场$u$， 流体的物理性质如何在这个速度场$u$下变化的计算我们称之为对流（advection）。一个最简单的对流方程，就是其物理量的物质导数为$0$，如下所示：
$$\frac{Dq}{Dt}=0⟹\frac{\partial q}{\partial t}+u\cdot \nabla q=0\text{\hspace{1em}(2.11)}$$
  公式$(2.11)$的意义即在拉格朗日视角观察下，每个流体粒子的物理量保持不变。

4、不可压缩性

  关于流体的压缩性在此不做过多的物理细节描述，只需知道一点：通常情况下流体的体积变化非常小（除开一些极端的情况，而且这些极端情况我们日常生活中较少出现）。可压缩流体的模拟涉及到非常复杂的情况，往往需要昂贵的计算资源开销，为此在计算机流体模拟中我们通常把所有的流体当作是不可压缩的，即它们的体积不会发生变化。

  任取流体的一部分，设其体积为$\Omega$而其边界闭合曲面为$\partial \Omega$，我们可以通过围绕边界曲面$\partial \Omega$对流体速度$u$在曲面法线方向上的分量进行积分来衡量这块部分流体的体积变化速率：
$$\frac{d}{dt}Volume(\Omega )=\int {\int }_{\partial \Omega }u\cdot n\text{\hspace{1em}(2.12)}$$
  对于不可压缩的流体，其体积保持为某个常量，故其体积变化速率为$0$：
$$\int {\int }_{\partial \Omega }u\cdot n=0\text{\hspace{1em}(2.13)}$$
  由高斯散度定理，我们可以把式$(2.13)$转换为体积分：
$$\int {\int }_{\partial \Omega }u\cdot n=\int \int {\int }_{\Omega }\nabla \cdot u=0\text{\hspace{1em}(2.14)}$$
  式$(13)$应该对任意的$\Omega$成立，意即无论$\Omega$取何值，积分值均为$0$。这种情况下只有令积分函数值取$0$方可成立，即对$0$积分无论$\Omega$取何值结果均为$0$。所以有：
$$\nabla \cdot u=0\text{\hspace{1em}(2.15)}$$
  这就是$Navier-Stokes$方程中的不可压缩条件$(2.2)$。满足不可压缩条件的速度场被称为是无散度的，即在该速度场下流体体积既不膨胀也不坍缩，而是保持在一个常量。模拟不可压缩流体的关键部分就是使得流体的速度场保持无散度的状态，这也是流体内部压力的来源。

  为了把压力与速度场的散度联系起来，我们在动量方程$(2.1)$两边同时取散度：
$$\nabla \cdot \frac{\partial u}{\partial t}+\nabla \cdot (u\cdot \nabla u)+\nabla \cdot \frac{1}{\rho }\nabla p=\nabla \cdot (g+\nu \nabla \cdot \nabla u)\text{\hspace{1em}(2.16)}$$
  对于上式$(2.16)$第一项，我们转变一下求导次序：
$$\frac{\partial }{\partial t}\nabla \cdot u\text{\hspace{1em}(2.17)}$$
  如果满足流体不可压缩条件，那么式$(2.17)$取值$0$（因为无散度），然后我们调整一下式$(2.16)$可得关于压力的方程：
$$\nabla \cdot \frac{1}{\rho }\nabla p=\nabla \cdot (-u\cdot \nabla u+g+\nu \nabla \cdot \nabla u)\text{\hspace{1em}(2.18)}$$

5、丢弃粘度项

  在某些流体如蜂蜜、小水珠等的模拟中，粘滞力起着非常重要的作用。但是在大多数流体动画模拟中，粘滞力的影响微乎其微，为此秉持着方程组越简单越好的原则，我们常常丢弃粘度项。当然这也不可避免地带来一些误差，事实上，在计算流体力学中尽可能地减少丢弃粘度项带来的误差是一个非常大的挑战。下面的叙述都是基于丢弃粘度项的前提。

  丢弃了粘度项的$Navier-Stokes$方程被称为欧拉方程，而这种理想的流体则是无粘度的。丢弃了粘度项的欧拉方程如下：
$$\frac{Du}{Dt}+\frac{1}{\rho }\nabla p=g\text{\hspace{1em}(2.19)}$$

$$\nabla \cdot u=0\text{\hspace{1em}(2.20)}$$

  大多数的流体模拟的计算方程都是欧拉方程。

6、边界条件

  目前为止我们讨论的都是流体内部的情况，然而边界部分也是流体模拟非常关键的部分。在流体模拟中我们仅仅关注两种边界条件：固体墙（solid walls）、自由面（free surfaces）。

  固体墙顾名思义就是流体与固体接触的边界，用速度来描述很简单：流体既不会流进固体内部也不会从固体内部流出，因此流体在固体墙法线方向上的分量为$0$：
$$u\cdot n=0\text{\hspace{1em}(2.21)}$$
  当然，上述是固体自身不移动的情况下。通常来说，流体速度在法线方向上的分量与固体的移动速度在法线方向上的分量应该保持一致：
$$u\cdot n=u_{solid}\cdot n\text{\hspace{1em}(2.22)}$$
  上述的两个公式都是仅对流体速度在法线方向上的分量做了限制，对于无粘度的流体，切线方向上的流体速度与固体的移动速度无必然的联系。

  自由面是另外一个非常重要的边界条件，它通常就是与另外一种流体相接壤的边界部分。例如在模拟水花四溅时，水流表面不与固体接触的都是自由面（如与空气这种流体接触）。因空气密度远小于水导致空气对水体的仿真影响非常小，为了简化模拟，我们将空气所占的空间设为某个固定大气压的区域，设为$0$是最方便的方案，此时自由面就是压强$p=0$的水体表面。

  在小规模的流体仿真中，自由面的表面张力占据着非常重要的地位。在微观分子层面下，表面张力的存在是因为不同的分子相互吸引产生的力。从几何的角度来解释就是，表面张力就是促使流体的表面积尽可能小的一种力。物理学上，两种不同的流体之间实际上存在着与表面平均曲率成正比的压力骤变：
$$[p]=\lambda k.\text{\hspace{1em}(2.23)}$$
  公式$(2.23)$中的$[p]$记为压力之差。$\lambda$是表面张力系数，可以根据模拟的流体类型查找对应的张力系数（例如空气与水在室温下张力系数为$\lambda \approx 0.073N/m$）。而$k$就是平均曲率，单位为$m^{-1}$。又因为我们常常设空气的压力为$0$，因此水与空气交界的自由面的压力为：
$$p=\lambda k\text{\hspace{1em}(2.24)}$$
​

三、N-S方程的分步求解

  有了对以上对$Navier-Stokes$方程的理论支撑，接下来我们就要如何用计算机来对该组偏微分方程进行离散化求解。为了程序的松耦合性以及使计算尽可能地高效、简单，在流体模型领域，我们将流体方程分成几个独立的步骤，然后按顺序先后推进。对于不可压缩的无粘度流体方程（即前面的欧拉方程$(2.19)$和$(2.20)$，我们将其离散化成对流项（advection）如公式$(3.1)$、体积力项（body force）如公式$(3.2)$、压力/不可压缩项如公式$(3.3)$：
$$\frac{Dq}{Dt}=0\text{\hspace{1em}(3.1)}$$

$$\frac{\partial u}{\partial t}=g\text{\hspace{1em}(3.2)}$$

$$\{\begin{array}{l}\frac{\partial u}{\partial t}+\frac{1}{\rho }\nabla p=0\\ \nabla \cdot u=0\end{array}\text{\hspace{1em}(3.3)}$$

  需要注意的是，在对流项公式$(3.1)$中我们用了一个通用量的符号$q$是因为我们不仅仅要对流体的速度进行对流，还需要对其他物理量进行对流。我们记对流项公式$(3.1)$的对流计算算法为$advect(u,\Delta t,q)$，即对于给定的时间步长$\Delta t$和速度场$u$，对物理量q进行对流。

  对于体积力项$(3.2)$，我们采用简单的前向欧拉法即可：$u\leftarrow u+g\Delta t$。

  对于压力/不可压缩项$(3.3)$，我们用一个称为$project(\Delta t,u)$的算法，通过$project(\Delta t,u)$计算出正确的压力以确保速度场$u$的无散度性质。欧拉方案不会着重研究具体粒子间的作用力，因而不会正向去求解$\frac{1}{\rho }\nabla p$，它是利用流体不可压缩的特性，将速度场$u$投影到散度为$0$的空间上，间接地解算了压力项。这种思想相当于，已知一个中间量$u_{temp}$，对这个中间量的唯一一个操作（如正向求解压力$\frac{1}{\rho }\nabla p$）不可行，但是直到最终量$u_{fianl}$符号的一个性质（散度为$0$），于是只要将$u_{temp}$投影到符合散度为$0$的特性平面上，即可间接地还原正向求解压力的操作，得到最终的速度场$u_{temp}$。

  对流项$advect(u,\Delta t,q)$的输入速度场$u$要确保为无散度的状态，投影项$project(\Delta t,u)$确保了流体体积保持不变，因而投影项输出的速度场必然是无散度的。所以我们只要确保投影项$project(\Delta t,u)$输出的速度场$u$作为对流项$advect(u,\Delta t,q)$的输入即可，这时我们的分步求解流体方程的优势就体现出来了，其伪代码如下所示。

---

算法1 Fluid Simulation($u_n$, $\Delta t$):

---

1: 初始化速度场$u_n$,使得$u_n$无散度

2: 对于每个时间步$n=0,1,2,...$

3:   决定一个合理的时间步长$\Delta t=t_{n+1}-t_n$

4:   对流项计算$u_A=advect(u_n,\Delta t,q)$

5:   体积力项计算$u_B=u_A+\Delta tg$

6:   无散度投影$u_{n+1}=project(\Delta t,u_B)$

---

1、时间步长

  在流体模拟算法中，确定适当的时间步长是算法的第一步。因为计算流体模拟的最后结果是呈现在屏幕上的，所以$\Delta t$的选取与屏幕的刷新率有重要的关系。若选取的$\Delta t$有$t_n+\Delta t>t_{frame}$，那么必须做一个截断使$\Delta t=t_{frame}-t_n$。此外，流体模拟的三个步骤即对流项、体积力项、无散度投影项对时间步长$\Delta t$的要求不尽相同，要选择一个满足所有要求的最小时间步长能确保计算的收敛性。此外，一方面为了流体模拟的真实性，我们可能需要选取一个足够小的时间步长来复现流体的高质量细节。另一方面，有时高性能的需求又使得我们不能选取太小的时间步长去渲染一帧。假设一帧至少要进行三个时间步的模拟，那么$\Delta t$应该至少设成帧间隔时间的三分之一。

2、网格结构

  欧拉法的整个流程都是基于网格的，所以合理的网格结构是算法高效的关键点。$Harlow$和$Welch$提出了一种经典的$MAC$（marker and cell）网格结构，许多不可压缩流体模拟的算法都在这个网格结构上呈现出了良好的效率。$MAC$网格是一种交叉排列的网格，不同类型的物理量被存储于网格的不同位置。以二维的网格为例，如图3-1左图所示，流体粒子的压力数据存储于网格的中心点$P_{i,j}$，而速度则沿着笛卡尔坐标被分成了两部分。水平方向的$u$成分被存储在了网格单元竖直边的中心处，例如网格单元$(i,j)$和$(i+1,j)$之间的水平速度记为$u_{i+1/2,j}$。垂直方向的$v$成分则被存储在了网格单元水平面的中心上。这样的存储方案十分有利于估算流体流进/流出某个网格单元的量。

图3-1 MAC网格,左图二维,右图三维   扩展到三维的情况，$MAC$网格同样是交错排列的结构网格，如图3-1右图所示。压力数值存储在立方体网格单元的中心，三个速度分量分别被记录在立方体网格单元的三个表面的中心点上。在数值计算时，这样的分配方式使得我们可以准确地采用中心差分法计算压力梯度和速度的散度，同时克服了中心差分法的一个普遍的缺点。一维的情况为例，在网格顶点位置$...,q_{i-1},q_i,q_{i+1}...$上估算量场$q$的导数，为了无偏（所谓无偏，就是不偏向左边或者右边）估计网格顶点$i$处的$\frac{\partial q}{\partial x}$，一种比较自然的方式就是采用一阶中心差分法： $$ (\frac{\partial q}{\partial x})_i\approx \frac{q_{i+1}-q_{i-1}}{2\Delta x} \tag {3.4} $$   公式$(3.4)$是无偏的，且精确度为$O(\Delta x^2)$。而前向欧拉差分法偏向右边且精确度只有$O(\Delta x)$： $$ (\frac{\partial q}{\partial x})_i\approx \frac{q_{i+1}-q_i}{\Delta x} \tag {3.5} $$   然而，公式$(3.4)$存在着一个非常严重的问题：网格点$i$的估算导数完全忽略了$q_i$的值。数学上，只有常数函数的一阶导数为零。但是公式$(3.4)$遇到了锯齿函数如$q_i=(-1)^i$时，它错误地将该类函数的导数估算为$0$，这种问题被称为零空间问题（null-space problem）。

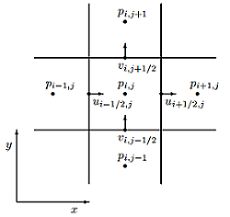
  交叉错排的$MAC$网格完美地克服了中心差分法的零空间问题，同时也保持了它的无偏二阶精度。在$MAC$网格上运用中心差分法，网格点$i$处的估算导数公式如下所示：
$$(\frac{\partial q}{\partial x}{)}_i\approx \frac{q_{i+1/2}-q_{i-1/2}}{\Delta x}\text{\hspace{1em}(3.6)}$$
  $MAC$网格确实给流体的压力计算和不可压缩性的处理带来了很大的便利，但与此同时也带来了一些其他方面的麻烦。如果我们要估算某个地方的速度向量，即便采样点恰好在网格点上我们也要做一些插值才能获取相应的速度向量。在网格点处，我们通常采用平均法，以二维为例：
$$\begin{gathered} u_{i,j}=(\frac{u_{i-1/2,j}+u_{i+1/2,j}}{2},\frac{v_{i,j-1/2}+v_{i,j+1/2}}{2}), \\ {u}_{i+1/2,j}=(u_{i+1/2,j},\frac{v_{i,j-1/2}+v_{i,j+1/2}+v_{i+1,j-1/2}+v_{i+1,j+1/2}}{4}), \\ {u}_{i,j+1/2}=(\frac{u_{i-1/2,j}+u_{i+1/2,j}+u_{i-1/2,j+1}+u_{i+1/2,j+1}}{4},v_{i,j+1/2}).\text{\hspace{1em}(3.7)} \end{gathered}$$
  最后，在实现中下标索引一般没有浮点数之说，前面直接采用$i+1/2$的记法是为了便于叙述。一般约定如下：
$$\begin{gathered} p(i,j,k)=p_{i,j,k}, \\ u(i,j,k)=u_{i-1/2,j,k}, \\ v(i,j,k)=v_{i,j-1/2,k}, \\ w(i,j,k)=w_{i,j,k-1/2}.\text{\hspace{1em}(3.8)} \end{gathered}$$
  因而对于$nx\times ny\times nz$分辨率的网格，压力数值存储在$nx\times ny\times nz$的数组中，速度的$u$成分存储在$(nx+1)\times ny\times nz$数组中，速度的$v$成分存储在$nx\times (ny+1)\times nz$数组中，速度的$w$成分存储在$nx\times ny\times (nz+1)$数组中。

四、对流算法

  求解如下所示的对流方程是流体模拟的关键一步：
$$\frac{Dq}{Dt}=0\text{\hspace{1em}(4.1)}$$
  我们把这个对流数值计算的算法记为：
$$q^{n+1}=advect(u,\Delta t,q^n)\text{\hspace{1em}(4.2)}$$
  公式$(4.2)$中的各个符号含义：

  $u$：在$MAC$网格上的离散化的速度场；

  $\Delta t$：时间步长；

  $q^n$：当前的物理量场$q$（如流体密度、速度、燃烧物浓度等）；

  $q^{n+1}$：经过对流后得到的新的量场。

  在这里要特别注意，输入对流算法的速度场$u$必须是无散度的，否则模拟结果会出现一些奇怪的失真现象。

1、半拉格朗日对流算法（Semi-Lagrangian Advection）

  一维情况下，对流方程$(4.1)$写成偏微分的形式如下：
$$\frac{\partial q}{\partial t}+u\frac{\partial q}{\partial x}=0\text{\hspace{1em}(4.3)}$$
  分别采用前向欧拉差分法计算对时间的偏导和中心差分法计算对空间的偏导，我们有：
$$\frac{q_i^{n+1}-q_i^n}{\Delta t}+u_i^n\frac{q_{i+1}^n-q_{i-1}^n}{2\Delta x}=0\text{\hspace{1em}(4.4)}$$
  转成以$q_i^{n+1}$为计算目标的显式公式，得：
$$q_i^{n+1}=q_i^n-\Delta t{u}_i^n\frac{q_{i+1}^n-q_{i-1}^n}{2\Delta x}\text{\hspace{1em}(4.5)}$$
  公式$(4.5)$看起来没什么问题，但是却存在非常严重的漏洞。首先，前向欧拉法被证明是无条件不稳定的空间离散方法：无论取多么小Δ?，随着时间步的推进，累积误差终将发散。即使使用更稳定的时间积分方法来取代前向欧拉方法，解决了时间上的PDE（Partial Differential Equation，偏微分方程）计算，空间上的PDE计算还是会带来重大的麻烦。标准中心差分方法不可避免地会出现的零空间问题，具有高频震荡性质的速度场对空间的导数被错误地计算为$0$或几乎为$0$，低离速度分量被分离出来，从而导致模拟效果中出现许多奇怪的高频摆动和震荡。

  针对这些问题，研究者们提出了一个解然不同的、更加简单和更具物理直观意义的半拉格朗日法。之所以叫半拉格朗日法，是因为这种方法是以拉格朗日视角去解决欧拉视角的对流方程（“半”字的由来）。假设我们的目标是求解网格点$x_G$的在第$n+1$个时间步时关于物理量$q$的新值，记为$q_G^{n+1}$。在拉格朗日的视角下，我们可以寻找在第$n+1$时间步之前，是空间中的哪一个点上的流体粒子在速度场$u$的作用下“流向”了$x_G$，我们记这个粒子在第$n$个时间步时的网格位置为$x_P$，则第$n+1$个时间步时$x_G$的$q_G^{n+1}$即为第$n$个时间步时$x_P$的$q_P^n$。如下图4-1为半拉格朗日对流法的示意图。

图4-1 半拉格朗日对流法

  半拉格朗日对流法的第一步就是要找出$x_P$，为此我们根据$x_G$做反向的追踪。粒子位置对时间的导数就是速度场：
$$\frac{dx}{dt}=u(x)\text{\hspace{1em}(4.6)}$$
  经过一个时间步长$\Delta t$之后，粒子由$x_P$移动到$x_G$。为了得到$x_P$，最简单的方法就是采用前向欧拉法进行倒推：
$$x_P=x_G-\Delta tu(x_G)\text{\hspace{1em}(4.7)}$$
  然而前向欧拉法只有一阶的精度，若在不改变$\Delta t$的情况下提高精度，我们可以采用高阶的龙格库塔法（Runge-Kutta method）。采用二阶的龙格库塔法如下所示：
$$\begin{gathered} x_{mid}=x_G-\frac{1}{2}\Delta tu(x_G), \\ {x}_P=x_G-\Delta tu(x_{mid}).\text{\hspace{1em}(4.7)} \end{gathered}$$
  倒推得到$\Delta t$之前的网格位置$x_P$一般不会恰好在网格顶点上，为此我们需要做些插值。三维模拟通常采用三线性插值，而二维的则采用双线性插值。
$$q_G^{n+1}=interpolate(q_n,x_P)\text{\hspace{1em}(4.8)}$$

2、边界情况

  若我们倒推得到的$x_P$仍然在流体的内部，那么做插值是完全没问题的。但若$x_P$在流体的边界之外呢？这种情况的出现的原因通常有两个：一个是$x_P$确确实实在流体的外部且即将流入流体内部，另一个是由前向欧拉法或龙格库塔法的数值计算方法带来的误差导致。

  在一种情况下，我们应该知道当流体流入时其携带的物理量，此时我们将这个外部流入的物理量作为返回值即可。例如，第$n$个时间步时的外部流体以速度$U$和温度$T$在第$n+1$个时间步时注入流体内部$x_G$的位置，那么$T_G^{n+1}$的值就为$T$。

  在第二种由误差导致的情况下，一个适当的策略就是根据边界上的最近点外推出所求得物理量。在模拟某些流体时，外推变得很简单。例如，在模拟烟雾时我们简单地假设烟雾流体外部即空气的速度风场为某个常数$U$（可能为$0$），这样边界上的速度场都取$U$。但还有一些必须根据流体内部的已知量外推出未知量，这时情况就变得比较复杂了。具体如何外推将在后面介绍，目前我们只需要知道大概的步骤：首先寻找边界上的最近点，然后在最近点的领域内插值获取相应的物理量场。

3、时间步长大小

  对任何一种数值计算方法的主要的考虑点就是它是否稳定。幸运的是，半拉格朗日对流法已经被证明是一种无条件稳定的算法：无论$\Delta t$取多大，它永远不会出现数值爆炸的现象。因为每一个新值$q$的确定，都是通过对旧值得插值，无论是线性插值、双线性插值还是三线性插值，$q$的大小都是处于插值点之间，不会得到比原来插值点更大或者更小的值，因而$q$是有上下界的。这使得我们可以尽情地根据所需的模拟质量和模拟效率去调整时间步长。

  但是在实践中，时间步长的大小也不能选得太过极端，否则会产生一些奇观的现象。Foster和Fekiw提出了一个对$\Delta t$的限制：流体粒子在$\Delta t$内的倒推轨迹最多经过某个常数个网格单元为宜，例如5个：
$$\Delta t\le \frac{5\Delta x}{u_{max}}\text{\hspace{1em}(4.9)}$$
  公式$(4.9)$中，$u_{max}$是速度场的最大值，我们可以简单地取 存储在网格中的最大速度值。一个更鲁棒的方法考虑了体积力（如重力、浮力等）对最大速度的影响：
$$u_{max}=max(|u^n|)+\Delta t|g|\text{\hspace{1em}(4.10)}$$
  将不等式$(4.9)$的最大值带入公式$(4.10)$，我们有：
$$u_{max}=max(|u^n|)+\frac{5\Delta x}{u_{max}}|g|\text{\hspace{1em}(4.11)}$$
  取一个简单的速度上界（简化了公式$(4.11)$），$u_{max}$：
$$u_{max}=max(|u^n|)+\sqrt{5\Delta xg}\text{\hspace{1em}(4.12)}$$
  这样确保了$u_{max}$始终为正，且避免公式$(4.9)$的除$0$错误。

  关于时间步长的讨论离不开$CFL$（以Courant、Friedrichs、Lewy三人的名字命名）条件。$CFL$条件是一个简单而直观的判断计算是否收敛的必要条件。它的直观物理解释就是时间推进求解的速度必须大于物理扰动传播的速度，只有这样才能将物理上所有的扰动俘获到。满足$CFL$条件意味着当$\Delta x$和$\Delta t$趋于取极限$0$时，数值计算所求的解就会收敛到原微分方程的解。

  对于半拉格朗日对流法，其满足$CFL$条件当且仅当在极限情况下，追踪得到的粒子轨迹足够逼近真实的轨迹。足够逼近的意思是经过正确的网格插值能够得到正确的依赖域（即差分格式的依赖域包含了原微分方程的依赖域），追踪的轨迹就会收敛到正确真实的轨迹。

  因而，对于采用标准的显式有限差分法的对流方程求解，为了保证收敛，我们要求$q^{n+1}$的新值是由以当前网格点为中心、以$C\Delta x$（$C$是一个小的整数常量）为半径的邻域范围内插值得到：
$$\Delta t\le C\frac{\Delta x}{|u|}\text{\hspace{1em}(4.13)}$$
  公式$(4.13)$中的$C$被称为$CFL$数，因而不等式$(4.9)$可以看成是公式$(4.13)$取$CFL$数为$5$得到。

4、数值耗散

  对流算法在对流获取新的物理量场$q_i^{n+1}$时会进行一些插值操作，插值不可避免地会平滑物理量场，这带来了一些数值耗散。一次两次的数值耗散不会由太大的影响，但是在流体模拟中我们会在每个时间步都进行对流运算，反反复复的平滑操作将数值耗散不断扩大，损失大量的流体细节。

  以一维的对流项计算为例，流体速度为常量$u>0$：
$$\frac{\partial q}{\partial t}+u\frac{\partial q}{\partial x}=0\text{\hspace{1em}(4.14)}$$
  假设$\Delta t<\frac{\Delta x}{u}$，即单个时间步长内粒子追踪轨迹长度小于单个网格单元的大小。我们的目标点是$x_i$，则倒推得到的粒子位置就落在了$[x_{i-1},x_i]$上的$x_i-\Delta tu$，然后进行线性插值得到$q_i^{n+1}$：
$$q^{n+1}=\frac{\Delta tu}{\Delta x}{q}_{i-1}^n+(1-\frac{\Delta tu}{\Delta x})q_i^n\text{\hspace{1em}(4.15)}$$
  将公式$(4.15)$整理一下，有：
$$q_i^{n+1}=q_i^n-\Delta tu\frac{q_i^n-q_{i-1}^n}{\Delta x}\text{\hspace{1em}(4.16)}$$
  公式$(4.16)$实际上正好就是采用时间上的前向欧拉差分法和空间上的单向有限差分法的欧拉方案，把$q_i^n$看成是$q^n$关于$x_i$的函数，对$q_{i-1}^n$进行泰勒级数展开：
$$q_{i-1}^n=q_i^n-(\frac{\partial q}{\partial x}{)}_i^n\Delta x+(\frac{{\partial }^{2}q}{\partial x^2}{)}_i^n\frac{\Delta x^2}{2}+O(\Delta x^3)\text{\hspace{1em}(4.17)}$$
  将公式$(4.17)$代入公式$(4.16)$，并做一些变量消去，可得：
$$q_i^{n+1}=q_i^n-\Delta tu(\frac{\partial q}{\partial x}{)}_i^n+\Delta tu\Delta x(\frac{{\partial }^{2}q}{\partial x^2}{)}_i^n+O(\Delta x^2)\text{\hspace{1em}(4.18)}$$
  在二阶截断误差的情况下，结合公式$(4.18)$和公式$(4.14)$，有：
$$\frac{\partial q}{\partial t}+u\frac{\partial q}{\partial x}=u\Delta x(\frac{{\partial }^{2}q}{\partial x^2})\text{\hspace{1em}(4.19)}$$
  右边就是对流方程计算时引入的额外类似粘度乘上系数$u\Delta x$的项。这也就是说，当我们采用简单的半拉格朗日法去求解无粘度的对流方程时，模拟的结果却看起来我们像时在模拟有粘度的流体。这就是数值耗散! 当然，当$\Delta x\to 0$时，这个数值耗散系数也会趋于$0$，所以取时间步无穷小时能够得到正确的模拟结果，但这需要耗费巨额的计算资源开销。我们通常模拟的流体大多数都是无粘度的，所以如何减少这个数值耗散是个至关重要的难题。

  一个简单有效的修复数值耗散的方法就是采用更加锐利的插值方法，从而尽可能地减少由插值带来的数值耗散。在一维的情况时，我们采用三次插值（cubic interpolant）如下公式$(4.21)$，而不是简单的一次线性插值$(4.20)$：
$$q\approx (1-s)x_i+s{x}_{i+1}\text{\hspace{1em}(4.20)}$$

$$\begin{gathered} q\approx [-\frac{1}{3}s+\frac{1}{2}{s}^2-\frac{1}{6}{s}^3]q_{i-1}+[1-s^2+\frac{1}{2}(s^3-s)]q_i \\ +[s+\frac{1}{2}(s^2-s^3)]q_{i+1}+[\frac{1}{6}(s^3-s)]q_{i+2}\text{\hspace{1em}(4.21)} \end{gathered}$$

  扩展到二维或者三维就是双三次插值（bicubic interpolation）或三三次插值（tricubic interpolation）。以二维情况为例，我们可以先沿着$x$轴做第一遍的三次插值如公式$(4.22)$，然后再沿着$y$轴做第二遍插值如公式$(4.23)$：
$$\begin{gathered} q_{j-1}=w_{-1}(s)q_{i-1,j-1}+w_0(s)+q_{i,j-1}+w_1(s)q_{i+1,j-1}+w_2(s)q_{i+2,j-1}, \\ {q}_j=w_{-1}(s)q_{i-1,j}+w_0(s)+q_{i,j}+w_1(s)q_{i+1,j}+w_2(s)q_{i+2,j}, \\ {q}_{j+1}=w_{-1}(s)q_{i-1,j+1}+w_0(s)+q_{i,j+1}+w_1(s)q_{i+1,j+1}+w_2(s)q_{i+2,j+1}, \\ {q}_{j+2}=w_{-1}(s)q_{i-1,j+2}+w_0(s)+q_{i,j+2}+w_1(s)q_{i+1,j+2}+w_2(s)q_{i+2,j+2}.\text{\hspace{1em}(4.22)} \end{gathered}$$

$$q=w_{-1}(t)q_{j-1}+w_0(t)q_j+w_1(t)q_{j+1}+w_2(t)q_{j+2}\text{\hspace{1em}(4.23)}$$

  当然也可以先沿着$y$轴，然后再沿着$x$轴做插值操作。