任意斜率的中点画线算法

一、中点画线算法的基本原理
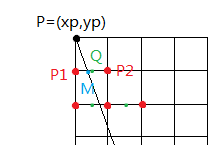
在画直线的过程中，当前像素点P(xp,yp)，则下一个点与直线最接近的像素只能是P1或者P2，即P点的正右方或者右上角的点。设M(xp+1,yp+0.5)为P1与P2的中点，Q为与理想直线与x=xp+1线相交的点。当M在Q的下方时，则P2应为下一像素点；当M在Q的上方时，则P1应为下一像素点。

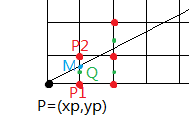
设直线的表达式 F(x+y)=ax+by+c，那么我们把M的数值代入到直线表达式中即可:
当 F（x，y） = 0 ，点在直线上，任意取P1或者P2都可以；
当 F（x，y） > 0 ，点在直线上方，取P1，P1坐标为（xp+1，yp）
当 F（x，y） < 0 ，点在直线下方，取P2，P2坐标为（xp+1，yp+1）
我们只需要判断F符号，可知Q点在中点M的上方还是下方，就可以判断下一个点是P1还是P2。

二、 中点画线算法的具体分类
1. 0<=k<=1

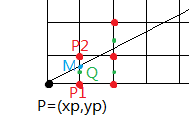
设当前点P(x_p,y_p)，则下一点P1和P2中点M点坐标为M(x_p+1,y_p+0.5)。
将M点带入F(x,y)：
d_0=F(M)=F(x_p+1,y_p+0.5)=a(x_p+1)+b(y_p+0.5)+c
此时分两种情况：
①若d_0<0,则取P2点，即右上点；
②若d_0>0,则取P1点，即正右点。
下面对两种情况进行分别讨论：
当d0<0时,即下一像素点为P2，下下一个像素点位置为M(xp+2,yp+1.5)：
d1=F(M)=F(xp+2,yp+1.5)=a(xp+1)+b(yp+0.5)+c+a+b=d0+a+b
当d0>0时,即下一像素点为P1，下下一个像素点位置为M(xp+2,yp+0.5)：
d1=F(M)=F(xp+2,yp+0.5)=a(xp+1)+b(yp+0.5)+c+a=d0+a
2. -1<=k<0

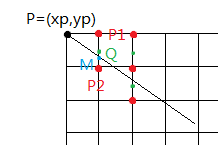
设当前点P(x_p,y_p)，则下一点P1和P2中点M点坐标为M(x_p+1,y_p-0.5)。
将M点带入F(x,y)：
d_0=F(M)=F(x_p+1,y_p-0.5)=a(x_p+1)+b(y_p-0.5)+c
此时分两种情况：
①若d_0<0,则取P1点，即正右点；
②若d_0>0,则取P2点，即右下点。
下面对两种情况进行分别讨论：
当d_0<0时,即下一像素点为P1，下下一个像素点位置为M(x_p+2,y_p-0.5)：
d_1=F(M)=F(x_p+2,y_p-0.5)=a(x_p+1)+b(y_p-0.5)+c+a=d_0+a
当d_0>0时,即下一像素点为P2，下下一个像素点位置为M(x_p+2,y_p-1.5)：
d_1=F(M)=F(x_p+2,y_p-1.5)=a(x_p+1)+b(y_p-0.5)+c+a-b=d_0+a-b
3. K>1

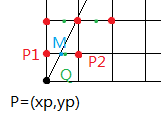
设当前点P(x_p,y_p)，则下一点P1和P2中点M点坐标为M(x_p+0.5,y_p+1)。
将M点带入F(x,y)：
d_0=F(M)=F(x_p+0.5,y_p+1)=a(x_p+0.5)+b(y_p+1)+c
此时分两种情况：
①若d_0<0,则取P1点，即正上点；
②若d_0>0,则取P2点，即右上点。
下面对两种情况进行分别讨论：
当d_0<0时,即下一像素点为P1，下下一个像素点位置为M(x_p+0.5,y_p+2)：
d_1=F(M)=F(x_p+0.5,y_p+2)=a(x_p+0.5)+b(y_p+1)+c+b=d_0+b
当d_0>0时,即下一像素点为P2，下下一个像素点位置为M(x_p+1.5,y_p+2)：
d_1=F(M)=F(x_p+1.5,y_p+2)=a(x_p+0.5)+b(y_p+1)+c+a+b=d_0+a+b
4. K<-1

设当前点P(x_p,y_p)，则下一点P1和P2中点M点坐标为M(x_p+0.5,y_p-1)。
将M点带入F(x,y)：
d_0=F(M)=F(x_p+0.5,y_p-1)=a(x_p+0.5)+b(y_p-1)+c
此时分两种情况：
①若d_0<0,则取P2点，即右下点；
②若d_0>0,则取P1点，即正下点。
下面对两种情况进行分别讨论：
当d_0<0时,即下一像素点为P2，下下一个像素点位置为M(x_p+1.5,y_p-2)：
d_1=F(M)=F(x_p+1.5,y_p-2)=a(x_p+0.5)+b(y_p-1)+c+a-b=d_0+a-b
当d_0>0时,即下一像素点为P1，下下一个像素点位置为M(x_p+0.5,y_p-2)：
d_1=F(M)=F(x_p+0.5,y_p-2)=a(x_p+0.5)+b(y_p-1)+c-b=d_0-b