算法分析与设计——分治法

\quad 所谓分治法，就是将一个问题分而治之。具体分为三个步骤

• 将问题划分为若干个子问题
• 递归求解每个子问题，注意写好递归边界
• 将若干子问题的解合并成问题的解

问题一、逆序对

\quad 给定一个序列，例如$a[5]=\{5,4,8,10,2\}$，找出这样的数对，$i<j,a[i]>a[j]$，例如这个例子包含(5,4),(5,2),(4,2),(8,2),(10,2) 5个逆序对。
\quad 我们用分治法思维来思考这个题，将序列等分为两段，将这两段分别排好序，那么逆序对数目就能够通过计算得到。例如$a=\{3,4,5\},b=\{2,3,7\}$，我们将这两个有序子序列合并成一个子序列的时候，当选择第一个数的时候得到2，发现a中第一个数比2大，那么a后面所有的数都比2大，那么与2组成逆序对的数目为3。利用此规律，对于每个子问题，我们可以在$O(n)$的时间复杂度内完成逆序对的计数。如何将序列划分为两段，并且使得它们有序呢？这就是天然的归并排序啊。

#include 
using namespace std;
const int maxn = 5e5+10;
int a[maxn], temp[maxn];
long long res = 0;  // 记录逆序对数目
void mergeSort(int left, int right)
{
    if(left<right)
    {
        int mid = (left+right)/2;
        mergeSort(left, mid);
        mergeSort(mid+1, right);
        int index = 0, i = left, j = mid+1;
        while(i<=mid && j<=right)
        {
            if(a[i]<=a[j]) temp[index++] = a[i++];
            else
            {
                temp[index++] = a[j++];
                res += mid-i+1; // 当a[i]>a[j]时形成逆序对，数目为左子序列长度减去i再加上1
            }
        }
        while(i<=mid) temp[index++] = a[i++];
        while(j<=right) temp[index++] = a[j++];
        for(int i = 0; i < index; i++) a[left+i] = temp[i];
    }
}
int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++) cin >> a[i];
    mergeSort(0, n-1);
    cout << res << endl;
    return 0;
}

问题二、最近点对

\quad 给定平面上n个点，求这n个点中距离最近的两个点的距离是多少。
\quad 暴力法：我们可以两两枚举任意两点间距离，取最小值，这样时间复杂度为$O(n^2)$，显然是不够优秀的。
\quad 分治法：我们将平面上的点划分为两部分，每部分$\frac{n}{2}$个点，递归求解两部分的最近点距离。难点在于子问题的合并，如下图所示，L为分界线，将n个点等分为两部分(将点按照x坐标排序后即可分开)。设左边部分最近点距离为$d_1=12$，右边部分最近点距离等于$d_2=21$，L分界线两边各取一个点计算得到的距离的最小值为$d_3$，那么合并的时候最近点距离$d=min(d_1,d_2,d_3)$。我们求$d_3$的时候无需枚举所有点，只需要枚举离分界线L横坐标差小于等于$\delta =min(d_1,d_2)$的点即可，这可以极大的减小运算量。同时再求$d_3$时，我们将横坐标位于$[L-\delta ,L+\delta ]$的点(图中深色带状区域)按照y轴排序，对于其中的某个点$p$，我们只需要计算里它横坐标距离不超过$\delta$的点即可(超出这个范围就不是最近距离了)。$T(n)=2T(\frac{n}{2})+nlogn,O(n)=n(logn{)}^2$。有$nlogn$的算法，改进点在于每次回溯要保留当前分别按照x，y轴排好序的坐标序列，这样在求$d_3$按照y坐标排序那一步的时候只需进行一遍merge即可，无需排序，$T(n)=2T(\frac{n}{2})+n,O(n)=nlogn$。

\quad 先放出程序，再一步一步解释。

#include 
#include 
#include 
using namespace std;

const int maxn = 1e6+1;
const int INF = 1<<30;
struct Point {
	double x, y;
}S[maxn];
int temp[maxn];
double distance(int i, int j)
{
	double x = (S[i].x-S[j].x)*(S[i].x-S[j].x);
	double y = (S[i].y-S[j].y)*(S[i].y-S[j].y);
	return sqrt(x+y);
}
// 按照x坐标排序，若x坐标一样，再按照y坐标排序
bool cmpx(const Point &a, const Point &b)
{
	if(a.x==b.x) return a.y<b.y;
	else return a.x<b.x;
}
// 按照y坐标排序
bool cmpy(const int &a, const int &b)
{
	return S[a].y < S[b].y;
}
double merge(int left, int right)
{
	double d=INF;
	if(left==right) return d;
	if(right-left==1) return distance(left, right);
	int mid = (left+right)/2;
	double d1 = merge(left, mid);  // 左边部分最短距离为d1
	double d2 = merge(mid+1, right); // 右边部分最短距离为d2
	d = min(d1, d2); // d为二者中较小者
	int index = 0;
	for (int i = left; i <= right; ++i)
	{
		// 选取位于分界线L横坐标距离不超过d的点(中间区域)
		if(abs(S[mid].x-S[i].x)<d) temp[index++] = i;
	}
	sort(temp, temp+index, cmpy); // 将中间区域内点按照y坐标排序
	for (int i = 0; i < index; ++i)
	{
		// 对于中间区域每个点，只需计算与它横坐标距离不超过d的点的距离
		// 根据鸽笼原理可知最多只需要枚举与当前点距离最近的8个点即可
		for (int j = i+1; (j<index)&&(j<i+9)&&(S[temp[j]].y-S[temp[i]].y)<d; ++j)
		{
			double d3 = distance(temp[i], temp[j]);
			if(d>d3) d = d3;
		}
	}
	return d;
}
int main()
{
	int n;  // 输入点数
	scanf("%d", &n);
	for (int i = 0; i < n; ++i)
	{
		scanf("%lf%lf", &S[i].x, &S[i].y);
	}
	sort(S, S+n, cmpx);
	double minDis = merge(0, n-1); // 得到问题的解
	printf("%.4lf\n", minDis);
	return 0;
}
/*
输入
10
1 1
1 5
3 1
5 1
5 6
6 7
7 3
8 1
9 3
9 9
输出
1.4142
*/

\quad 接下来，我用上面程序中给出的例子来绘图详解一下。这组样例是排好序的，我们可以得到这样的图

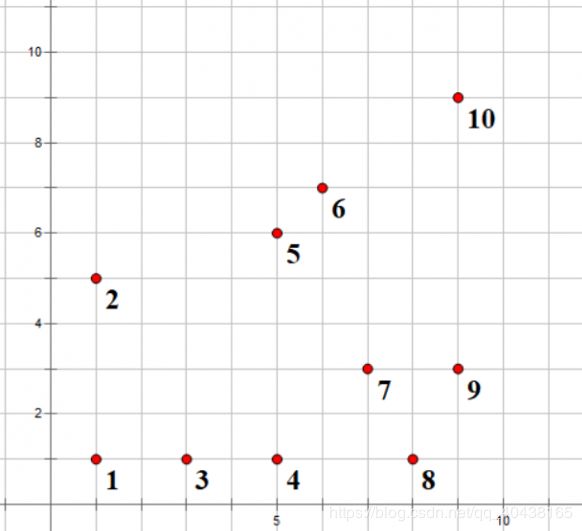
\quad 下面我们要开始merge()了，merge(left,right)是返回由编号left∼right的点构成的最近点对的距离，所以merge(1, n)即为答案，因为这是一个递归函数，我们假设它已经能返回一个区域中的最近点对了。

double d=INF;
if(left==right) return d;
if(right-left==1) return distance(left, right);

\quad 然后算出mid并进行递归，mid即为图中那条线L

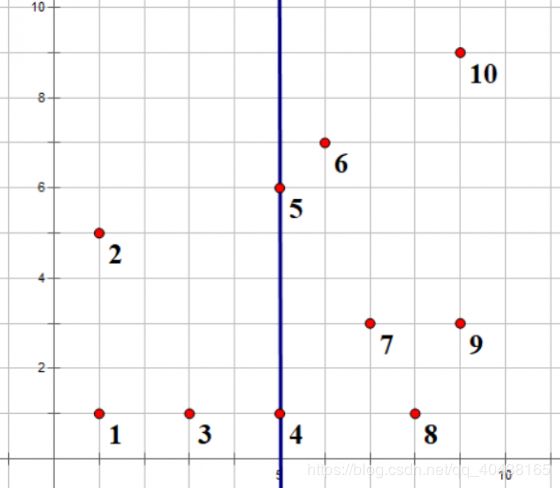
\quad 也就是求出[1∼5]和[6∼10]中的最近点对，显然$d_1=2(1和3),d_2=\sqrt{5}(7和8)$，那么$d=min(d_1,d_2)=2$。

int mid = (left+right)/2;
double d1 = merge(left, mid);  // 左边部分最短距离为d1
double d2 = merge(mid+1, right); // 右边部分最短距离为d2
d = min(d1, d2); // d为二者中较小者

\quad 接下来就是这个算法的核心，如何求出跨越蓝线的最近点对了，首先锁定点集temp，temp为$[L-d,L+d]$区间内点的集合

int index = 0;
for (int i = left; i <= right; ++i)
{
	// 选取位于分界线L横坐标距离不超过d的点(中间区域)
	if(abs(S[mid].x-S[i].x)<d) temp[index++] = i;
}

\quad 将temp按照y坐标排序，对于temp内每一个点，我们只需要枚举部分点，这部分点需要同时满足下列2个条件。这步优化非常重要！

• 1.只需要枚举与当前点距离不超过d的点的距离即可
• 2.根据鸽笼原理可知最多只需要枚举与当前点距离最近的8个点即可

如果新计算出的两点间距离小于d，则更新d为该值。

sort(temp, temp+index, cmpy); // 将中间区域内点按照y坐标排序
	for (int i = 0; i < index; ++i)
	{
		// 对于中间区域每个点，只需计算与它横坐标距离不超过d的点的距离
		// 根据鸽笼原理可知最多只需要枚举与当前点距离最近的8个点即可
		for (int j = i+1; (j<index)&&(j<i+9)&&(S[temp[j]].y-S[temp[i]].y)<d; ++j)
		{
			double d3 = distance(temp[i], temp[j]);
			if(d>d3) d = d3;
		}
	}

\quad 至此，我们完成求解，返回$and=\sqrt{2}=1.4142(5和6)$。

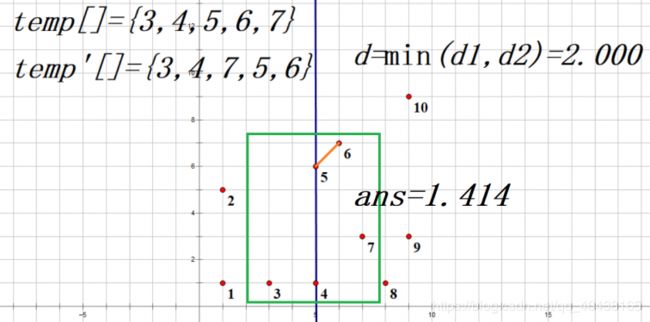
\quad 实测在评测机上，20w个点能在100ms跑完，很优秀的算法。对于中间区域内某个点，计算与之最近点的距离，若只采用只枚举与之最近的8个点，需要120ms，若只枚举与之y轴距离不超过d的点，需要170ms，两者同时使用，减小到100ms。