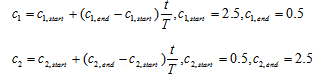Matlab粒子群算法（PSO）优化程序——调整权重、改进学习因子

粒子群算法（ Particle Swarm Optimization, PSO）在应用的过程中主要调整权重，学习因子，才能对解决的问题有所针对性。下面有6种调整权重和学习因子：
一、调整粒子群算法的权重
1.线性递减权重
2.自适应调整权重
3.随机权重
二、调整粒子群算法的学习因子
1.收缩因子
2.同步学习因子
3.异步学习因子
目标函数如下：

function y=A11_01(x)

y=x(1)^2+x(2)^2-x(1)*x(2)-10*x(1)-4*x(2)+60;

一、调整粒子群算法的权重
1.线性递减权重
Shi.Y认为较大的权重惯性有利于全局搜索，较小的权重有利于局部搜索，他提出的线性递减权重刚好满足这样的需求。

一般而言，k为当前迭代次数，T为最大迭代次数。

%粒子群 PSO  线性递减权重
clear 
clc

%%预设参数
n=100;
d=2; %变量个数
c1=2;
c2=2;
w=0.9;
K=100;
ws=0.9;
we=0.4;

%%分布粒子
x=-10+20*rand(n,d);
v=-5+10*rand(n,d);

%%计算适应度
fit=zeros(n,1);
for j=1:n
    fit(j)=A11_01(x(j,:));
end
%计算个体极值
pbest=x;
ind=find(min(fit)==fit);
gbest=x(ind,:);

%%更新速度与位置
for i=1:K
    for m=1:n
       v(m,:)=w*v(m,:) + c1*rand*(pbest(m,:)-x(m,:)) + c2*rand*(gbest-x(m,:));
       w=ws-(ws-we)*(i/K);
       
       v(m,find(v(m,:)<-10))=-10;
       v(m,find(v(m,:)>10))=10;
       
       x(m,:)=x(m,:)+0.5*v(m,:);
       x(m,find(x(m,:)<-10))=-10;
       x(m,find(x(m,:)>10))=10;
       
       %重新计算适应度
       fit(m)=A11_01(x(m,:));
       if x(m,:)

图1 线性递减权重的迭代优化过程

2.自适应调整权重
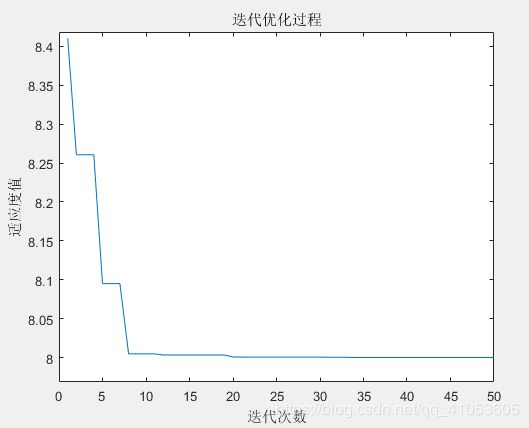
自适应权重：权重随着粒子适应度值的改变而改变。

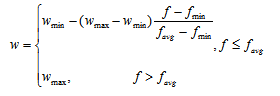
%%自适应调整权重
clear all;
clc;

%%预设参数
n=100;
d=2; %变量个数
c1=2;
c2=2;
K=20;
wmax=0.9;
wmin=0.4;

%%分布粒子
x=-10+20*rand(n,d);
v=-5+10*rand(n,d);

%%计算适应度
fit=zeros(n,1);
for j=1:n
    fit(j)=A11_01(x(j,:));
end
%计算个体极值
pbest=x;
ind=find(min(fit)==fit);
gbest=x(ind,:);

%%更新速度与位置
for i=1:K
    for m=1:n
        f=fit(m);
        favg=sum(fit)/n;
        fmin=min(fit);
        if f<=favg
            w=wmin-(wmax-wmin)*(f-fmin)/(favg-fmin);
        else
            w=wmax;
        end
       v(m,:)=w*v(m,:) + c1*rand*(pbest(m,:)-x(m,:)) + c2*rand*(gbest-x(m,:));
       
       v(m,find(v(m,:)<-10))=-10;
       v(m,find(v(m,:)>10))=10;
       
       x(m,:)=x(m,:)+0.5*v(m,:);
       x(m,find(x(m,:)<-10))=-10;
       x(m,find(x(m,:)>10))=10;
       
       %重新计算适应度
       fit(m)=A11_01(x(m,:));
       if x(m,:)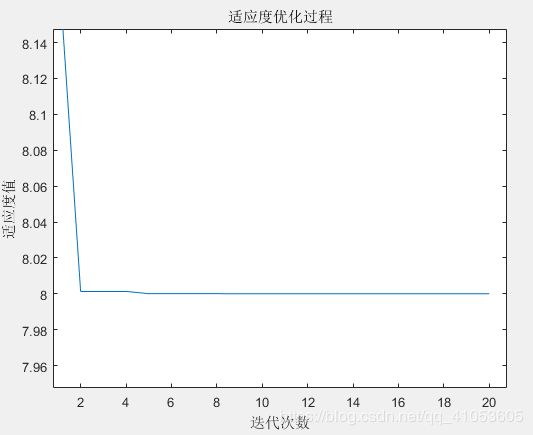

图2 自适应调整权重的迭代过程
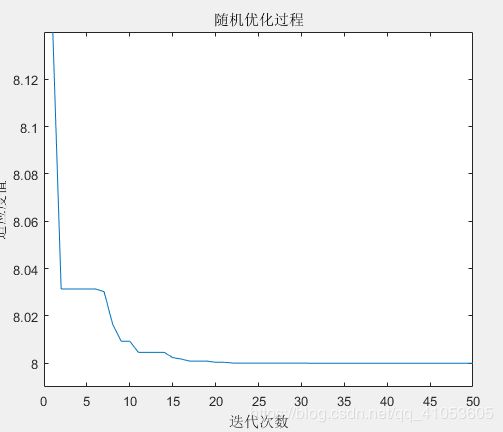
3.随机权重
当粒子在起始位置接近最优点时，可能产生较小权重。

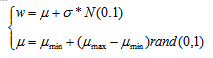
%%随机权重
clear all;
clc;

%%预设参数
n=100;
d=2; %变量个数
c1=2;
c2=2;
K=50;
wmax=0.8;
wmin=0.5;
delta=0.5;

%%分布粒子
x=-10+20*rand(n,d);
v=-5+10*rand(n,d);

%%计算适应度
fit=zeros(n,1);
for j=1:n
    fit(j)=A11_01(x(j,:));
end
%计算个体极值
pbest=x;
ind=find(min(fit)==fit);
gbest=x(ind,:);

%%更新速度与位置
for i=1:K
    for m=1:n
      miu=wmin+(wmax-wmin)*rand;
      w=miu+delta*randn;
       v(m,:)=w*v(m,:) + c1*rand*(pbest(m,:)-x(m,:)) + c2*rand*(gbest-x(m,:));
       
       v(m,find(v(m,:)<-10))=-10;
       v(m,find(v(m,:)>10))=10;
       
       x(m,:)=x(m,:)+0.5*v(m,:);
       x(m,find(x(m,:)<-10))=-10;
       x(m,find(x(m,:)>10))=10;
       
       %重新计算适应度
       fit(m)=A11_01(x(m,:));
       if x(m,:)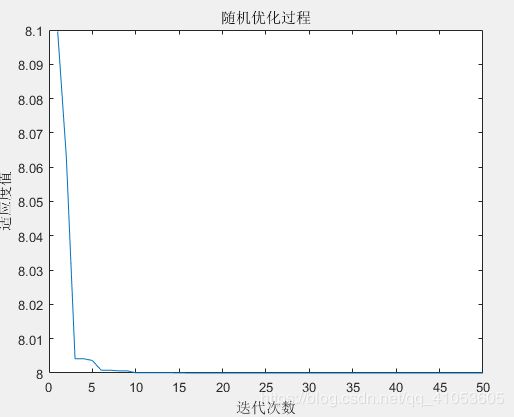

图3 随机权重的迭代过程
二、调整粒子群算法的学习因子
1.收缩因子

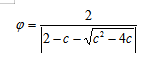
c=c1+c2,c>4,一般c=4.1.

%%收缩因子
clear all;
clc;

%%预设参数
n=100;
d=2; %变量个数
c1=2.05;
c2=2.05;
K=20;
w=1;
C=4.1;
fai=2/abs((2-C-sqrt(C^2-4*C)));

%%分布粒子
x=-10+20*rand(n,d);
v=-5+10*rand(n,d);

%%计算适应度
fit=zeros(n,1);
for j=1:n
    fit(j)=A11_01(x(j,:));
end
%计算个体极值
pbest=x;
ind=find(min(fit)==fit);
gbest=x(ind,:);

%%更新速度与位置
for i=1:K
    for m=1:n
     v(m,:)=fai*(w*v(m,:) + c1*rand*(pbest(m,:)-x(m,:)) + c2*rand*(gbest-x(m,:)));
       
       x(m,:)=x(m,:)+0.5*v(m,:);
       x(m,find(x(m,:)<-10))=-10;
       x(m,find(x(m,:)>10))=10;
       
       %重新计算适应度
       fit(m)=A11_01(x(m,:));
       if x(m,:)

图4 收缩因子的迭代过程`

2.同步学习因子

%%同步学习因子
clear all;
clc;

%%预设参数
n=100;
d=2; %变量个数
K=50;
w=0.9;
cmax=2.1;
cmin=0.8;

%%分布粒子
x=-10+20*rand(n,d);
v=-5+10*rand(n,d);

%%计算适应度
fit=zeros(n,1);
for j=1:n
    fit(j)=A11_01(x(j,:));
end
%计算个体极值
pbest=x;
ind=find(min(fit)==fit);
gbest=x(ind,:);

%%更新速度与位置
for i=1:K
    for m=1:n
       c1=cmax-(cmax-cmin)*(i/K);
       c2=c1;
       v(m,:)=w*v(m,:) + c1*rand*(pbest(m,:)-x(m,:)) + c2*rand*(gbest-x(m,:));
       v(m,find(v(m,:)<-10))=-10;
       v(m,find(v(m,:)>10))=10;
       
       x(m,:)=x(m,:)+0.5*v(m,:);
       x(m,find(x(m,:)<-10))=-10;
       x(m,find(x(m,:)>10))=10;
       
       %重新计算适应度
       fit(m)=A11_01(x(m,:));
       if x(m,:)

图 5 同步学习因子的迭代过程
3.异步学习因子

%%异步学习因子
clear all;
clc;

%%预设参数
n=100;
d=2; %变量个数
K=50;
w=0.9;
cstart1=2.5;
cend1=0.5;
cstart2=0.5;
cend2=2.5;

%%分布粒子
x=-10+20*rand(n,d);
v=-5+10*rand(n,d);

%%计算适应度
fit=zeros(n,1);
for j=1:n
    fit(j)=A11_01(x(j,:));
end
%计算个体极值
pbest=x;
ind=find(min(fit)==fit);
gbest=x(ind,:);

%%更新速度与位置
for i=1:K
    for m=1:n
       c1=cstart1+(cend1-cstart1)*(i/K);
       c2=cstart2+(cend2-cstart2)*(i/K);
       v(m,:)=w*v(m,:) + c1*rand*(pbest(m,:)-x(m,:)) + c2*rand*(gbest-x(m,:));
       v(m,find(v(m,:)<-10))=-10;
       v(m,find(v(m,:)>10))=10;
       
       x(m,:)=x(m,:)+0.5*v(m,:);
       x(m,find(x(m,:)<-10))=-10;
       x(m,find(x(m,:)>10))=10;
       
       %重新计算适应度
       fit(m)=A11_01(x(m,:));
       if x(m,:)

图 6 异步学习因子

Matlab粒子群算法（PSO）优化程序的优点在于参数数量比较少，调整权重和改进学习因子都是比较好进行的。
注：函数来源于https://www.51zxw.net/show.aspx?id=71576&cid=641。