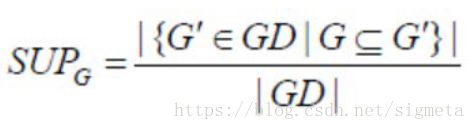【数据挖掘学习笔记】10.频繁模式挖掘基础

一、基本概念

频繁模式

– 频繁的出现在数据集中的模式

– 项集、子序或者子结构

动机

– 发现数据中蕴含的事物的内在规律

• 项(Item) 

– 最小的处理单位 – 例如：Bread, Milk

• 事务(Transaction) 

– 由事务号和项集组成 – 例如：<1, {Bread,Milk}> 

• 事务数据库 

– 由多个事务组成

• 项集(Itemset)

– 一个或多个项(item) 的集
    • 例如：{Milk, Bread, Diaper}
– k-项集(k-itemset)

    • 包含k个项的集合

• 包含关系

– 令T为一事务，P为一项集，如果P是T的子集，称T包含P ，记T⊇P或P⊆T
    • 例如{Milk, Bread, Diaper} ⊆T4

• 关联规则(Association Rule)

– 项的集合：I={i1,i2,...,in}
– 任务相关数据D是数据库事务的集合，每个事务T则是项的集合，使得T ⊆ I
– 每个事务由事务标识符TID标识；
– A,B为两个项集，事务T包含A当且仅当A ⊆ T
– 则关联规则是如下蕴涵式：
    • A →B (s, c)
    • 其中，A和B 都是项集，s是规则的支持度，c是置信度

• 支持度计数(Support count)

– 事务数据库中包含某个项集的事务的个数

– 例如：σ({Milk, Bread,Diaper}) = 2

• 支持度(Support)

– 事务数据库中包含某个项集的事务占事务总数的比例。

支持度s是指事务集D中包含A ∪ B的百分比

support(A ⇒ B) = P(A ∪ B)

置信度c是指D中包含A的事务同时也包含B的百分比

confidence (A ⇒ B) = P(B | A) = P(A ∪ B)/ P(A)

• 关联规则挖掘目的

– 给定一个事务数据库TD，关联规则挖掘的目标是要找到所有支持度和置信度都不小于指定阈值的规则。
    • 支持度≥minsup
    • 置信度≥minconf

• 关联规则步骤：

– 1、找个这个“同一项集”，相同的项集对应的规则有相同的支持度，找到支持度≥minsup的项集
– 2、计算项集中所有规则的置信度，找到置信度≥minconf的规则

• 频繁项集(Frequent Itemset)

– 令P为任何一个项集，如果P的支持度不小于指定的最小阈值(minsupthreshold)，称P为频繁项集

关联规则挖掘分类

– 根据挖掘的模式的完全性分类：给定min_sup，可以挖掘频繁项集的完全集，闭频繁项集和极大频繁项集。也可以挖掘被约束的频繁项集（即满足用户指定的一组约束的频繁项集）、近似的频繁项集（只推导被挖掘的频繁项集的近似支持度计数）、接近匹配的频繁项集（即与接近或几乎匹配的项集的支持度计数符合的项集）、top-k频繁项集
– 不同的应用对挖掘的模式的完全性有不同的要求，我们主要研究挖掘频繁项集的完全集、闭频繁项集和被约束的频繁项集

二、Apriori

生成频繁项集

穷举法(Brute-force approach) 

– 每个项集都是候选的频繁项集
– 通过扫描一次事务数据库，可以得到每个候选项集的支持度
    • 比较每一条事务和每个候选项集

– 计算复杂度－O(NMw
    • N为事务数目，M = 2d为候选项集，d为项数，w为一次比较的计算

• 计算复杂度－O(NMw)
    – 太高，需要改进
• 改进策略
    – 缩小候选项集的数量(M)
        • 完全搜索：M=2d
        • 通过裁减技术减少M
    – 缩小比较次数(NM)
        • 用不同的数据结构来存储后续项集和事务
        • 避免比较每一对候选项集和事务
    – 缩小比较代价(w)

• 缩小候选集

– Apriori性质:
    • 如果一个项集是频繁的，那么它的所有子集都是频繁的。
    • 也称为反单调性
– Apriori性质成立的原因如下
    • 任何一个项集的支持度不可能超过其子集的支持度

缩小候选集思路

Apriori算法

– Apriori算法是挖掘布尔关联规则频繁项集的算法
– Apriori算法利用频繁项集性质的先验知识（prior knowledge），通过逐层搜索的迭代方法，即将k-项集用于探察(k+1)-项集，来穷尽数据集中的所有频繁项集。
– 先找到频繁1-项集集合L1,然后用L1找到频繁2-项集集合L2，接着用L2找L3，直到找不到频繁k-项集，找每个Lk需要一次数据库扫描。

计算候选集支持度

方法：
– 用hash树来存储候选项集
– hash树的叶子结点包含候选项集及其计数
– 非叶结点包含hash table
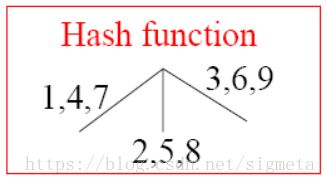
– hash函数：找出包含在一个事务中的所有候选项集

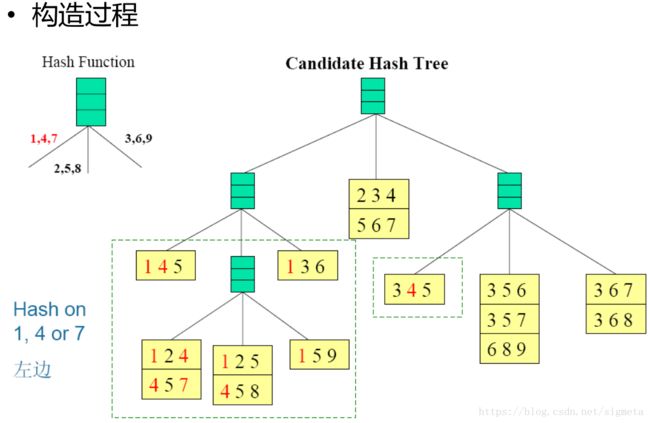
构造Hash树
– 假定有15个长度为3的候选项集：{1 4 5}, {1 2 4}, {4 5 7}, {1 2 5}, {4 5 8}, {1 5 9}, {1 3 6}, {2 3 4}, {5 6 7}, {3 4 5}, {3 5 6}, {3 5 7}, {6 8 9}, {3 6 7}, {3 6 8}
– 设定：
    • Hash函数
    • 最大叶结点尺寸：在一个叶结点中存储的最大候选项集的数目（如果大于该阈值则分裂该结点）

候选集
– {1 4 5}, {1 2 4}, {4 5 7}, {1 2 5}, {4 5 8}, {1 5 9}, {1 3 6}, {2 3 4}, {5 6 7}, {3 4 5}, {3 5 6}, {3 5 7}, {6 8 9}, {3 6 7}, {3 6 8}
– 哈希树

子集操作

查找哈希树

Apriori算法主要的挑战 

– 要对数据进行多次扫描； 

– 会产生大量的候选项集； 

– 对候选项集的支持度计算非常繁琐； 

解决思路 

– 减少对数据的扫描次数； 

– 缩小产生的候选项集； 

– 改进对候选项集的支持度计算方法

• 方法1：基于hash表的项集计数

– 将每个项集通过相应的hash函数映射到hash表中的不同的桶中，这样可以通过将桶中的项集技术跟最小支持计数相比较先淘汰一部分项集。

• 方法2：事务压缩（压缩进一步迭代的事务数）
– 不包含任何k-项集的事务不可能包含任何(k+1)-项集，这种事务在下一步的计算中可以加上标记或删

• 方法3：划分
– 挖掘频繁项集只需要两次数据扫描
– D中的任何频繁项集必须作为局部频繁项集至少出现在一个部分中。
    • 第一次扫描：将数据划分为多个部分并找到局部频繁项集
    • 第二次扫描：评估每个候选项集的实际支持度，以确定全局频繁项集

• 方法4：选样（在给定数据的一个子集挖掘）
– 基本思想：选择原始数据的一个样本，在这个样本上用Apriori算法挖掘频繁模式
– 通过牺牲精确度来减少算法开销，为了提高效率，样本大小应该以可以放在内存中为宜，可以适当降低最小支持度来减少遗漏的频繁模式
    • 可以通过一次全局扫描来验证从样本中发现的模式
    • 可以通过第二此全局扫描来找到遗漏的

• 方法5：动态项集计数
– 在扫描的不同点添加候选项集，这样，如果一个候选项集已经满足最少支持度，则在可以直接将它添加到频繁项集，
而不必在这次扫描的以后对比中继续计算.

Apriori算法每次循环都要扫描一遍数据库，用来计算候选项集的支持度。随着项集长度增加，候选项集的个数逐渐减少，包含这些候选项集的事务也越来越少，但是扫描的事务量并没有改变。
– 提高效率的方法：在后续循环中逐渐减少扫描的事务。

AprioriTid

– 基本定理
• 如果一个事务不包含频繁k-项集，那么该事务必然不包含频繁(k+1)-项集。
– 由以上定理可知，把不包含频繁k-项集的事务删除后，不会影响计算长度更长（>k）的项集的支持度。
– 基于上述思想构成了AprioriTid算法

• AprioriTid基本思想

– 在产生候选项集之后，构造一个Tid表，用来记录每个事务包含的候选项集。候选k-项集的Tid表记做Ck，其形式为，其中，Tid是事务t的标识，C是事务t中包含的候选k-项集。如果一个事务不包含任何候选k-项集，则这个事务就不会出现在Ck中。
– 对于k＝1，C1 ＝TD；
– 对于k >1，Ck由Ck－1生成
    • 如果一个事务包含了一个候选k-项集的两个频繁(k－1)-项集，那么其必然包含这个候选k-项集。
    • 故构造Ck的方法如下：
        – 对每个候选k-项集P，如果P的两个频繁(k－1)-项集都包含在Ck－1里的某个记录中，则添加P到Ck的相应记录中。

示例

AprioriTid算法

– 优点
    • 用逐渐减少的Tid表代替原来的事务数据库
– 缺点
    • 在初始阶段，尤其是第二次循环（发现频繁2-项集），候选项集的个数非常多，导致构造的Tid表可能比原事务数据库还要大很多。这时Apriori在效率上要优于AprioriTid
– AprioriHybral
    • 结合Apriori和AprioriTid的优点
    • 思想
        – 首先采用Apriori算法，同时估计Tid表的大小。
        – 当Tid表减小到可以载入内存时，就转而采用AprioriTid算法

减少候选集数目
– Apriori算法的复杂性与候选项集的数目有关，候选项集越多，构造的hash树越大，运行时间就越长，因此，提高Apriori算法的另外一个途径就是减少候选项集数目。
    • Apriori算法在构造候选k-项集的时候利用了频繁k-1项集进行裁减，有效地降低了候选项集的数量。
    • 但是这个方法对生成候选2-项集基本上没有太大作用。
        – 令频繁1-项集个数为n，则候选2-项集个数为n(n-1)/2

三、频繁图挖掘

频繁子图挖掘

– 若干图中找到最大的频繁子图

标号图

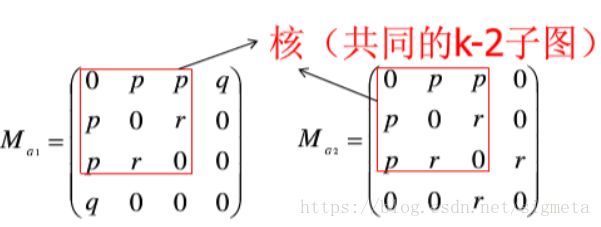
– 一个标号图是一个五元组,G={V,E,ΣE,ΣV,L}.其中,V代表图中节点的集合,E⊆V×V代表图中边的集合.ΣV,ΣE分别代表节点标号的集合与边标号的集合.L是标号函数,用于完成标号向节点和边的映射:V→ΣV与E→ΣE. 

图的同构

– 图的同构是一个双射f:V(G)↔V(G′).对于图G={V,E,ΣV,ΣE,L}与图G′={V′,E′,ΣV′,ΣE′, L′},若它们是同构的,则满足如下条件: 
    • ∀u∈V,L(u)=L′(f(u)) 
    • ∀u,v∈V,((u,v)∈E)⇔((f(u),f(v))∈E′),且
    • ∀(u,v)∈E,L(u,v)=L′(f(u),f(v)). 

支持度

– 给定一个图的集合GD,图G的支持度记为SUPG,计算方法为GD中与G存在子图同构的图G′的个数与整个图集中图的个
数的比值,表示如下: 

频繁图/频繁树

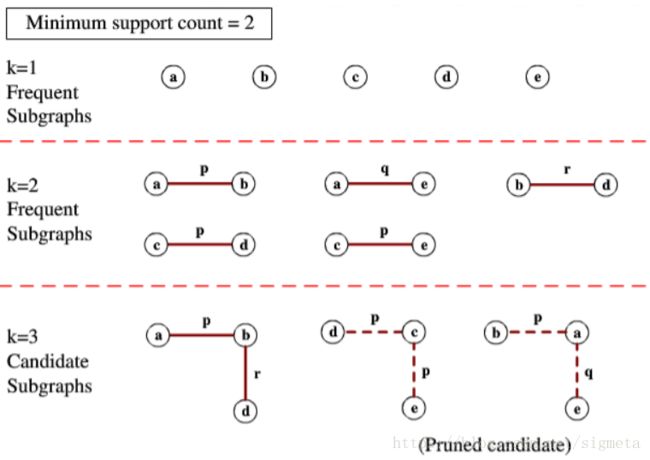
– 给定一个图集GD,GD={Gi|i=0,1,…,n},且给定最小支持度阈值为min_sup,我们称图G是频繁的,当且仅当G的支持度不小于最小支持度阈值,即SUPG≥min_sup.相应地,当图G是频繁的且其中无回路时,我们称G为频繁树

类Apriori算法

例

变种
– 点一致，边一致
– 点一致，边不一致（例如小于即可）
– 点不一致，边一致
– 点，边都不一致，连接关系一致