Bresenham 画线算法推导过程
今天复习这个算法的时候,有一点没有立马反应过来,故特此记此篇博客作为备忘。
文章目录
- 描点原理
- 用 $p_i$ 代替 $d_1 - d_2$
- $p_i$ 递推
- 如何确定 $p_1$ 呢?
- 程序代码
描点原理
原理就是描实距离D点最近的那个点,距离的判断通过比较d1和d2的大小来确定。d1大,说明距离 ( x i + 1 , y i ) (x_i + 1, y_i) (xi+1,yi)更远,要描实 ( x i + 1 , y i + 1 ) (x_i + 1, y_i + 1) (xi+1,yi+1)。相反同理。
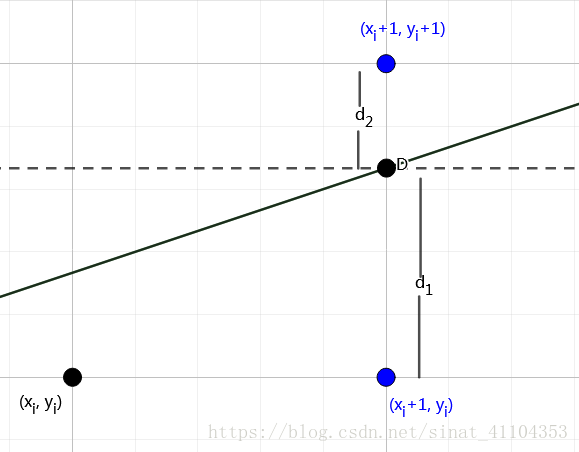
需要说明的是此图将横线和竖线的交点看作像素点。
不妨假设直线方程为 y = kx + b ,其斜率 k 在 0 到 1 之间,并且 x 2 > x 1 x_2>x_1 x2>x1。
于是我们可以有上图这样一条直线。设在第 i 步已经确定第 i 个像素点是 ( x i , y i ) (x_i, y_i) (xi,yi),现在看第 i+1 步如何确定第 i+1 个像素点的位置:
我们不妨假设 D(x, y) 其中 x = x i + 1 x = x_i+1 x=xi+1
d 1 = y − y i = k ( x i + 1 ) + b − y i d_1 = y - y_i = k(x_i + 1) + b -y_i d1=y−yi=k(xi+1)+b−yi
d 2 = y i + 1 − y = ( y i + 1 ) − k ( x i + 1 ) − b d_2 = y_i + 1 - y = (y_i + 1) - k(x_i + 1) - b d2=yi+1−y=(yi+1)−k(xi+1)−b
- d 1 > d 2 d_1 > d_2 d1>d2,下一个像素点取 ( x i + 1 , y i + 1 ) (x_i + 1, y_i + 1) (xi+1,yi+1)
- d 1 < d 2 d_1 < d_2 d1<d2,下一个像素点取 ( x i + 1 , y i ) (x_i + 1, y_i) (xi+1,yi)
- d 1 = d 2 d_1 = d_2 d1=d2,取两个像素点中的任意一个
我们知道判断 d 1 和 d 2 d_1 和d_2 d1和d2 大小可以通过作差来得出。
d 1 − d 2 = 2 k ( x i + 1 ) − 2 y i + 2 b − 1 d_1 - d_2 = 2k(x_i + 1) - 2y_i + 2b - 1 d1−d2=2k(xi+1)−2yi+2b−1,其中的 k 值为 Δ y Δ x \dfrac{\Delta{y}}{\Delta{x}} ΔxΔy,其中 Δ x \Delta{x} Δx 为 x 2 − x 1 x_2 - x_1 x2−x1, Δ y \Delta{y} Δy 为 y 2 − y 1 y_2 - y_1 y2−y1。
用 p i p_i pi 代替 d 1 − d 2 d_1 - d_2 d1−d2
这里有个问题是,k 值是通过除法得出来的,我们知道计算机计算除法都是不精确的,所以这里,我们要做一点处理,来避免除法运算。这里,我们做的是两边同乘 Δ x \Delta{x} Δx
Δ x ( d 1 − d 2 ) = 2 Δ y ( x i + 1 ) − Δ x ⋅ 2 y i + Δ x ⋅ ( 2 b − 1 ) \Delta{x}(d_1 - d_2) = 2\Delta{y}(x_i + 1) - \Delta{x}·2y_i + \Delta{x}·(2b - 1) Δx(d1−d2)=2Δy(xi+1)−Δx⋅2yi+Δx⋅(2b−1)
由于 Δ x \Delta{x} Δx 在我们假设的时候就是大于0的,于是 d 1 − d 2 d_1 - d_2 d1−d2 的符号并不会因此而改变,于是我们不妨假设 p i = Δ x ( d 1 − d 2 ) p_i = \Delta{x}(d_1 - d_2) pi=Δx(d1−d2)。
p i = 2 Δ y ( x i + 1 ) − Δ x ⋅ 2 y i + Δ x ⋅ ( 2 b − 1 ) p_i = 2\Delta{y}(x_i + 1) - \Delta{x}·2y_i + \Delta{x}·(2b - 1) pi=2Δy(xi+1)−Δx⋅2yi+Δx⋅(2b−1)
我们将其中不变的一部分提取出来,并用常数 c 来代替:
p i = 2 Δ y ⋅ x i − 2 Δ x ⋅ y i + c p_i = 2\Delta{y}·x_i - 2\Delta{x}·y_i + c pi=2Δy⋅xi−2Δx⋅yi+c
这样,我们就可以通过判断 p i p_i pi 的正负来判断是描哪个点。
- p i ⩾ 0 p_i \geqslant 0 pi⩾0,即 d 1 ⩾ d 2 d_1 \geqslant d_2 d1⩾d2,选取右边的点,此时 y i + 1 = y i + 1 y_{i+1} = y_i + 1 yi+1=yi+1
- p i < 0 p_i < 0 pi<0,即 d 1 < d 2 d_1 < d_2 d1<d2, 选取右上的点,此时 y i + 1 = y i y_{i+1} = y_i yi+1=yi
p i p_i pi 递推
当然,我们仅仅知道一个 p i p_i pi 是不够的,我们得进一步的递推下去:
p i + 1 = 2 Δ y ⋅ x i + 1 − 2 Δ x ⋅ y i + 1 + c p_{i+1} = 2\Delta{y}·x_{i+1} - 2\Delta{x}·y_{i+1} + c pi+1=2Δy⋅xi+1−2Δx⋅yi+1+c
这里的 p i + 1 p_{i+1} pi+1 代表下下一个描点的判别式。
通过做一个减法,我们可以得出 p i + 1 和 p i p_{i+1} 和 p_i pi+1和pi 之间的数值关系:
p i + 1 − p i = 2 Δ y − 2 Δ x ( y i + 1 − y i ) p_{i+1} - p_i = 2\Delta{y} - 2\Delta{x}(y_{i+1} - y_i) pi+1−pi=2Δy−2Δx(yi+1−yi)
于是我们可以得出下面结论:
- p i ⩾ 0 p_i \geqslant 0 pi⩾0,应取 y i + 1 = y i + 1 y_{i+1} = y_i + 1 yi+1=yi+1, 带入得 p i + 1 = p i + 2 ( Δ y − Δ x ) p_{i+1} = p_i + 2(\Delta{y} - \Delta{x}) pi+1=pi+2(Δy−Δx)
- p i < 0 p_i < 0 pi<0,应取 y i + 1 = y i y_{i+1} = y_i yi+1=yi , 带入得 p i + 1 = p i + 2 Δ y p_{i+1} = p_i + 2\Delta{y} pi+1=pi+2Δy
我们通过 p i p_i pi 的正负选出下个点,然后判断 p i p_i pi 和 p i + 1 p_{i+1} pi+1 的关系,以此来求出 p i + 1 p_{i+1} pi+1 的值。再通过 p i + 1 p_{i+1} pi+1 的正负选出下个点,然后推出 p i + 1 p_{i+1} pi+1 和 p i + 2 p_{i+2} pi+2 的关系。
如何确定 p 1 p_1 p1 呢?
x 1 = x 1 x_1 = x_1 x1=x1, y 1 = Δ y Δ x x 1 + b y_1 = \dfrac{\Delta{y}}{\Delta{x}}x_1 + b y1=ΔxΔyx1+b => Δ x ⋅ y 1 = Δ y ⋅ x 1 + Δ x ⋅ b \Delta{x}·y_1 = \Delta{y}·x_1 + \Delta{x}·b Δx⋅y1=Δy⋅x1+Δx⋅b
在 p i p_i pi 的公式中,不妨令 i = 1,有:
p i = 2 Δ y ( x i + 1 ) − Δ x ⋅ 2 y i + Δ x ⋅ ( 2 b − 1 ) p_i = 2\Delta{y}(x_i + 1) - \Delta{x}·2y_i + \Delta{x}·(2b - 1) pi=2Δy(xi+1)−Δx⋅2yi+Δx⋅(2b−1)
p 1 = 2 Δ y ( x 1 + 1 ) − Δ x ⋅ 2 y 1 + Δ x ⋅ ( 2 b − 1 ) p_1 = 2\Delta{y}(x_1 + 1) - \Delta{x}·2y_1 + \Delta{x}·(2b - 1) p1=2Δy(x1+1)−Δx⋅2y1+Δx⋅(2b−1)
将刚才推导出来的式子带入化简得:
p 1 = 2 Δ y − Δ x p_1 = 2\Delta{y} - \Delta{x} p1=2Δy−Δx
程序代码
void BresenhamLine(int x1, int y1, int x2, int y2)
{
int x, y, dx, dy, p; //dx和dy是Δx和Δy
x = x1;
y = y1;
dx = x2 - x1;
dy = y2 - y1;
p = 2*dy - dx;
for (; x <= x2; x++) {
SetPixel(x, y);
if (p > 0) {
y++;
p += 2*(dy-dx);
} else {
p += 2*dy;
}
}
}